7. Интеграл Эйлера–Пуассона

Определение. Несобственный интеграл называется интегралом Эйлера–Пуассона.

Известно, что не выражается через элементарные функции,

поэтому для вычисления интеграла Эйлера–Пуассона используем двойной интеграл от функции по различным специального вида областям.

Рассмотрим три области:

1. – 1-я четверть круга радиуса R; x²+y² ≤ R²(x ≥ 0; y ≥ 0).

2. – квадрат со стороной R в 1-й четверти; x=R; y=R; x=0; y=0.

3. – 1-я четверть круга радиуса : x²+y² ≤ 2R²(x ≥ 0; y ≥ 0).

По каждой из этих областей вычислим двойной интеграл .

1. 

2. 

3. 

Так как при любых (x; y) D и , то:

Следовательно:

Так как и положительны при любых значениях R, то

.

Вычислим пределы:

По теореме о пределе трёх функций: .

8. Некоторые приложения двойного интеграла

1) Площадь плоской области D:

.

2) Объём цилиндрического тела, ограниченного сверху поверхностью , снизу областью D на плоскости 0XY, сбоку цилиндрической поверхностью, параллельной оси 0Z (рис. 1):

.

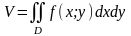3) Площадь поверхности :

,

где – проекция данной поверхности на плоскость 0XY.

4) Масса пластинки, занимающей область D плоскости 0XY и имеющей плотность :

.

При этом статистические моменты пластинки относительно осей 0X и 0Y:

; .

2. Координаты центра тяжести пластинки:

.

В случае однородной пластинки и координаты центра тяжести однородной пластинки имеют вид:

.

§2. Тройной интеграл

1. Определение тройного интеграла

Пусть задана функция на замкнутой области D R³.

Определение 1. Сумма 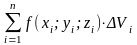, где точка , – объём i-й части разбиения области D на , называется интегральной суммой функции в области D. Определение 2. Тройным интегралом от функции по области D R³ называется предел интегральной суммы при условиях:

а) и (стягиваясь в точку);

б) этот предел существует и не зависит ни от способа разбиения области D на части , ни от выбора точек в области .

Итак:

где – элемент области D R³.

Теорема (достаточное условие существования тройного интеграла)

Если функция непрерывна в области D R³, то тройной интеграл от этой функции по области D существует.

2. Физический и геометрический смысл тройного интеграла

1) Если при D R³, то тройной интеграл от такой функции по области D равен объёму тела D:

2) Если в каждой точке объёмной области D задана плотность распределения масс , то тройной интеграл от этой плотности по области D равен массе тела, занимающего область D:

.

3. Основные свойства тройного интеграла

1) Если функция непрерывна в объёмной области D и , то

.

2) Если k постоянная величина, то

.

3) Если функции и непрерывны в области D R³, то

.

4. Если для любых значений D R³ выполняется неравенство: , то

.

Теорема (о среднем значении тройного интеграла)

Если функция непрерывна в замкнутой области D R³, то внутри области D найдётся хотя бы одна точка , для которой выполняется равенство:

где – объём тела, занимающего область D.

4. Вычисление тройного интеграла в декартовой системе координат

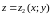Для вычисления тройного интеграла от функции по области D R³ проецируем область D на плоскость 0XY. Обозначим эту проекцию . Пусть область D будет такой, что любая прямая, проходящая через внутреннюю точку области D параллельно оси 0Z, пересекает поверхность S, ограничивающую область D, только в двух точках. Пусть и – уравнения поверхностей, ограничивающих область D снизу и сверху соответственно (рис. 1).

Тогда можно записать:

Рис. 1

Если область G окажется правильной в направлении, например, оси 0Y, т.е. , то

Замечание 1. При сведении тройного интеграла к трём повторным интегралам не обязательно проецировать область D на плоскость 0XY, можно проецировать либо на 0XZ, либо на 0YZ – как удобнее. Замечание 2. Следует сначала вычислять внутренний интеграл по z, считая x и y постоянными, а затем вычислять двойной интеграл от полученной функции по области G, тогда:

Пример. Вычислить

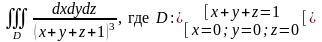
Рис. 2

Объёмная область D – треугольная пирамида с основанием AOB и вершиной в точке C (рис. 2). Пр – треугольник AOB.

Ответ:

5. Вычисление тройного интеграла в цилиндрических координатах

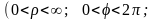
Переход от декартовых координат к цилиндрическим проводится по формулам: (рис. 3). . Тогда тройной интеграл от по области 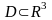преобразуется следующим образом:

Рис. 3

6. Вычисление тройного интеграла в сферических координатах

Переход от декартовых координат к сферическим проводится по формулам (рис. 4):

Рис. 4

Тогда тройной интеграл от по области D R³ преобразуется следующим образом:

7. Некоторые приложения тройного интеграла

1) Объём тела, занимающего область D R³:

2) Масса тела, занимающего область D R³:

,

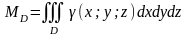где – плотность тела.

3) Координаты центра тяжести тела, занимающего область D R³:

Если тело однородное, т.е. , то координаты его центра тяжести:

§ 3. Криволинейные интегралы

1. Криволинейные интегралы I рода (по дуге)

Пусть функция z = f (x; y) определена и непрерывна в точках дуги AB, принадлежащей гладкой кривой l, имеющей уравнение . Разобьём дугу AB произвольным образом на n дуг точками 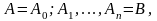пусть – длина дуги . На каждой из n дуг выберем произвольно точку и умножим значение функции в этой точке на длину .

Определение 1. Интегральной суммой для функции f (x; y) по дуге AB называется сумма вида: . Определение 2. Криволинейным интегралом от функции f (x; y) по дуге AB (или криволинейным интегралом I рода) называется предел интегральной суммы вида

при условиях:

1) ; 2) этот предел существует и не зависит ни от способа разбиения дуги AB на части, ни от выбора на каждой из частей точек .

Криволинейный интеграл I рода вычисляется по формуле:

если кривая AB задана функцией .

Если кривая AB задана параметрически: x = x(t), y = y(t), где , то криволинейный интеграл I рода от функции по такой кривой вычисляется по формуле:

Аналогично определяется и вычисляется криволинейный интеграл от функции , определенной и непрерывной в точках дуги AB гладкой пространственной кривой l. Пусть эта кривая задана параметрическими уравнениями: x = x(t), y = y(t), z = z(t) ( ), тогда

Если , то криволинейный интеграл I рода представляет собой массу кривой l, имеющей переменную плотность .