13. Метод найменших квадратів (мнк). Система нормальних рівнянь.

Нехай треба знайти аналітичний вигляд функції 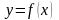, яка добре відображала б цю таблицю дослідних даних. Функцію можна шукати у вигляді інтерполяційного поліному. Формулу 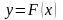називають емпіричною, або рівнянням регресії на .

Процес побудови емпіричних формул складається з двох етапів: встановлення загального виду цієї формули і визначення найкращих її параметрів.

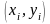
Щоб встановити вигляд емпіричної формули, на площині будують точки з координатами . Підбирають найпростіші функції: лінійну, квадратичну, дробово-раціональну, степеневу, показникову, логарифмічну.

Найточніші значення коефіцієнтів емпіричної формули визначають методом найменших квадратів.

Розглянемо суть методу найменших квадратів.

Нехай емпірична формула має вигляд

, (1)

де 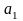, , …, ─ невідомі коефіцієнти. Треба знайти такі значення коефіцієнтів 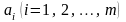, за яких крива (1) якомога ближче проходитиме до всіх 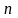точок 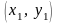, , 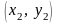…, , знайдених експериментально. За методом найменших квадратів найкращі значення коефіцієнтів ті, для яких сума квадратів відхилень

(2)

дослідних даних від обчислених за емпіричною формулою (1) найменша. Звідси випливає, що величина (2), яка є функцією від коефіцієнтів , повинна мати мінімум. Необхідна умов мінімуму функції багатьох змінних ─ її частинні похідні мають дорівнювати нулю, тобто

, , …, .

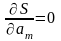Диференцюючи вираз (2) по невідомих параметрах , матимемо відносно них систему рівнянь:

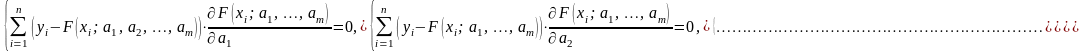
Система називається нормальною. Якщо вона має розв’язок, то він єдиний.

Будуючи емпіричні формули, припускатимемо, що експериментальні дані додатні.

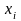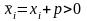Якщо серед значень і є від’ємні, то завжди можна знайти такі додатні числа і , що і .

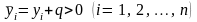Тому розв’язування поставленої задачі завжди можна звести до побудови емпіричної формули для додатних значень .

14. Оператор оцінювання мнк в матричному вигляді.

Нехай економетрична модель у матричній формі має вигляд

Тоді суму квадратів залиш­ків u можна записати так:

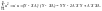
Продиференціюємо цю умову за А і прирівняємо похідні до нуля:

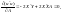
або

_(4.6)

Тут — матриця, транспонована до матриці незалежних змінних X.

Звідси

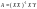(4.7)

Рівняння (4.6) дає матричну форму запису системи нормальних рівнянь, а формула (4.7) показує, що значення вектора А є розв’язком системи таких рівнянь.

Неважко показати, що оцінки В, обчислені за (4.7), мінімізують суму квадратів залишків u. При цьому значення вектору В є розв’язком так званої системи нормальних рівнянь

.

Якщо незалежні змінні в матриці X взяті як відхилення кожного значення від свого середнього, то матрицю називають матрицею моментів.

Числа, що розміщені на її головній діагоналі, характеризують величину дисперсій незалежних змінних, інші елементи відповідають взаємним коваріаціям.Отже, структура матриці моментів відбиває зв’язки між незалежними змінними. Чим ближчі показники коваріацій до величини дисперсій, тим ближчий визначник матриці 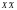до нуля і тим гірші оцінки параметрів 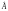. Далі буде показано, що стандартні помилки параметрів прямо пропорційні до значень, розміщених на головній діагоналі матриці .
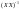