
- •Поняття економетричної моделі, її складові частини.
- •Причини, які спонукають появу випадкової складової в регресійних моделях.
- •Етапи побудови економетричної моделі.
- •Параметри моделі парної лінійної регресії, їх сутність та оцінювання.
- •Закони розподілу ймовірностей емпіричних параметрів , їх числові характерстики та статистичні властивості.
- •Обчислення значень вибіркових дисперсій , , для парної регресії.
- •Незміщені статистичні оцінки для , , в моделі парної лінійної регресії.
- •Коефіцієнт детермінації та кореляції для моделі парної регресії. Перевірка суттєвості коефіцієнта детермінації за допомогою t-критерію.
- •Коефіцієнт детермінації та кореляції для моделі парної регресії. Перевірка суттєвості коефіцієнта детермінації за допомогою f-критерію.
- •Перевірка суттєвості оцінок параметрів на основі t-критерію.
- •Точковий та інтервальний прогноз на основі побудованої моделі парної регресії.
- •Передумови застосування методу найменших квадратів.
- •Метод найменших квадратів (мнк). Система нормальних рівнянь.
- •Оператор оцінювання мнк в матричному вигляді.
- •Властивості оцінок параметрів, знайдених за мнк.
- •Дисперсійний аналіз моделі лінійної множинної регресії.
- •Коефіцієнт множинної кореляції та детермінації та перевірка їх статистичної значущості.
- •Дисперсійно-коваріаційна матриця оцінок параметрів.
- •Довірчі інтервали для оцінок параметрів.
- •Перевірка достовірності оцінок параметрів за допомогою t -критерію.
- •Точковий та інтервальний прогноз на основі побудованої моделі лінійної множинної регресії.
- •Перевірка загальної якості моделі та рівності двух коефіціентів детермінації.
- •Поліноміальна модель. Визначення вектора статистичний аналіз моделі.
- •Аналіз моделі.Показникова модель. Визначення вектора статистичний аналіз моделі.
- •Виробнича функція Кобба-Дугласа. Визначення вектора статистичний аналіз моделі.
- •Поняття фіктивних змінних.
- •Врахування якісних факторів в лінійних економетричних моделях за допомогою фіктивних змінних.
- •Моделі з фіктивними регресорами: моделі, що містять тільки фіктивні незалежні змінні та моделі, що містять як фіктивні, так і кількісні незалежні змінні.
- •Моделі з фіктивними залежними змінними.
- •Оцінювання параметрів моделі з фіктивними змінними.
- •Порівняння двох регресійних моделей. Тест Чоу.
- •Суть та наслідки мультиколінеарності.
- •Тестування наявності мультиколінеарності в моделі. Алгоритм Фаррара-Глобера.
- •Методи усунення мультиколінеарності.
- •Алгоритм покрокової регресії.
- •Поняття про гомо- та гетероскедастичність залишків.
- •Негативні наслідки наявності гетероскедастичності залишків в лінійних моделях.
- •Тест Гольдфельда-Квандта. Послідовність його виконання.
- •Алгоритм теста Глейсера.
- •Перевірка наявності гетероскедастичності залишків на основі теста коефіцієнта рангової кореляції Спірмена.
- •Узагальнений метод найменших квадратів для моделі з гетероскедастичністю залишків.
- •Зважений метод найменших квадратів.
- •Суть та наслідки автокореляції стохастичної складової.
- •Алгоритм Дарбіна-Уотсона для виявлення автокореляції залишків першого порядку.
- •Критерій фон Неймана.
- •Циклічний та нециклічний коефіцієнт автокореляції.
- •Узагальнений метод найменших квадратів для знаходження оцінок параметрів моделі з автокорельованими залишками.
- •Метод перетворення вихідної інформації.
- •Алгоритм методу Кочрена – Оркатта.
- •Оцінювання параметрів моделі з автокорельованими залишками методом Дарбіна.
- •Поняття часового лагу. Моделі з часовим лагом незалежних змінних.
- •Оцінювання авторегресійних моделей з часовим лагом незалежних змінних.
- •Часовий ряд в загальному вигляді. Поняття тренду, сезонної, циклічної та випадкової компоненти. Основні етапи аналізу числових рядів.
- •Метод ковзної середньої для згладжування часового ряду.
- •Експоненціальне згладжування.
- •Аналітичні методи згладжування часового ряду.
- •Довжина часового ряду суттєво перевищує ступінь полінома , а випадкові залишки мають властивості «білого шуму», тобто
- •Стаціонарні та нестаціонарні часові ряди. Основні характеристики часових рядів.
- •Тест Дікі-Фулера.
- •Авторегресійні моделі ( ar(p)- процеси).
- •Моделі ковзного середнього (ma(q)- процеси).
- •Авторегресійні моделі ковзного середнього ( arma(p,q)- процеси).
- •Інтегровані авторегресійні моделі ковзного середнього ( arima(p,d,q)- процеси).
- •Адаптивні моделі. Схема їх побудови.
- •Поняття про коінтеграцію часових рядів.
- •Моделі коригування помилки, етапи її побудови.
- •Поняття системи економетричних рівнянь. Приклади моделей на основі системи одночасних рівнянь.
- •Структурна та зведена форми системи рівнянь.
- •Ідентифікація. Необхідна і достатня умова ідентифікації.
- •Непрямий метод найменших квадратів оцінювання параметрів системи одночасних рівнянь.
- •Оцінювання параметрів системи одночасних рівнянь двохкроковим методом найменших квадратів.
- •Трьохкроковий метод найменших квадратів.
- •Прогноз ендогенних змінних
Поняття системи економетричних рівнянь. Приклади моделей на основі системи одночасних рівнянь.
Наявність прямих і зворотних зв’язків між економічними показниками вимагає побудови економетричної моделі на основі системи рівнянь.
Приклад. Нехай треба побудувати економетричну модель, яка характеризує залежність між обсягом валового національного продукту від виробничих ресурсів: основних виробничих фондів, робочої сили і матеріальних ресурсів. У такому разі доцільно будувати економетричну модель на основі системи одночасних структурних рівнянь:
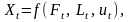

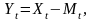
де
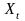 -
випуск продукції;
-
випуск продукції;
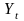 -
валовий національний продукт;
-
валовий національний продукт;
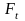 - основні виробничі фонди;
- основні виробничі фонди;
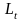 -
робоча сила;
-
робоча сила;
 -
матеріальні ресурси;
-
період часу.
-
матеріальні ресурси;
-
період часу.
Запишемо два перших рівняння аналітично:


де
,
,
,
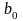 ,
,
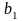 - параметри моделі,
,
- залишки.
- параметри моделі,
,
- залишки.
Отже, економетрична модель складається з трьох одночасних рівнянь, два перших є регресійними, а третє — тотожність. Оскільки вони описують економічні процеси, які відбуваються одночасно, то всі ці рівняння повинні мати спільний розв’язок.
Структурна та зведена форми системи рівнянь.
Економетрична модель у вигляді безпосередньо відображає структуру зв’язків між змінними і тому називається структурною формою економетричної моделі.
Розв’яжемо систему рівнянь відносно yst і дістанемо систему виду:
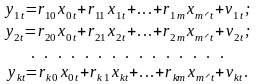 (12.3)
(12.3)
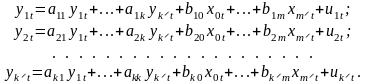
У матричній формі систему цих рівнянь можна переписати так:
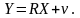
Матриця оцінок параметрів R має вигляд:
 (12.4)
(12.4)
де E - одинична матриця.
Щоб показати справедливість співвідношення (12.4), розв’яжемо систему рівнянь (12.2) відносно Y:
Y – AY = BX + u;
(E – A)Y = BX + u;
Y = (E – A)–1BX + u.
Враховуючи, що Y = RX + v, R = (E – A)–1B.
Вектор залишків
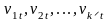 є лінійною комбінацією залишків
є лінійною комбінацією залишків
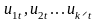 .
.
Економетрична модель, яка записується системою рівнянь (12.3), називається зведеною формою моделі.
Ідентифікація. Необхідна і достатня умова ідентифікації.
Проблеми чисельної оцінки параметрів в структурній формі і можливість перетворення структурної форми на зведену тісно пов’язані з поняттям ідентифікації моделі.
Необхідна умова ідентифікації системи - справедливість нерівності для кожного рівняння моделі
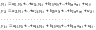

де
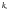 — кількість залежних ендогенних
змінних, які входять в s-те
рівняння структурної форми;
— кількість залежних ендогенних
змінних, які входять в s-те
рівняння структурної форми;
m — загальна кількість екзогенних змінних моделі;
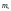 — кількість
екзогенних змінних, які входять в s-те
рівняння структурної форми моделі.
— кількість
екзогенних змінних, які входять в s-те
рівняння структурної форми моделі.
Число
екзогенних змінних, які не входять у
s-те
рівняння структурної форми, дорівнює
 .
.
Зауважимо, що прoблема ідентифікації стосується структурних параметрів, а не параметрів зведеної форми.
Альтернативна умова ідентифікації була записана нами в (11.10):
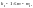 яка
потребує, щоб
число виключених із рівняння екзогенних
змінних було
не меншим, ніж число ендогенних
змінних мінус
одиниця.
яка
потребує, щоб
число виключених із рівняння екзогенних
змінних було
не меншим, ніж число ендогенних
змінних мінус
одиниця.
