Вопросы для самоконтроля

1. Запишите функцию Лагранжа задачи 12 в общем и безразмерном виде. Поясните роль и физический смысл безразмерного параметра.

2. Запишите уравнение движения задачи 12, следующее из уравнения Лагранжа.

3. Проведите полный анализ потенциальной энергии в задаче 12. Поясните характер движения при различных значениях безразмерного параметра и различных начальных условиях.

4. Как выглядят фазовые портреты задачи 12 при g < g_cr и g > g_cr?

5. Как определяется период нелинейных колебаний?

6. Определите частоты гармонических колебаний задачи 12 вблизи устойчивых положений равновесия при различных значениях безразмерного параметра.

7. Запишите функцию Гамильтона и уравнения движения в форме канонических уравнений задачи 12.

8. Запишите и решите уравнение Гамильтона-Якоби задачи 12, получив полный интеграл и закон движения. Как выглядит закон движения в канонических переменных?

13. Частица на вращающейся окружности в поле тяжести

Здесь конкурирует центробежная сила (задача 5 модуля 1) с силой тяжести (задача 7 модуля 1). Поэтому потенциальная энергия складывается из потенциальной энергии плоского математического маятника U_пмм(φ) = - mgRcosφ и центробежной потенциальной энергии, пропорциональной квадрату расстояния частицы до оси вращения U_cfg(φ) = - (mω²R²sin²φ)/2. Поэтому функция Лагранжа системы имеет вид

,

где U(φ) = U_пмм(φ) + U_cfg(φ) - полная потенциальная энергия.

Выбор масштабов массы и длины очевиден

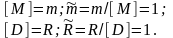
Имеется два масштаба времени – масштаб вращения [T]_ = 1/ и масштаб колебаний в поле тяжести . Для определенности за единицу выберем масштаб колебаний в поле тяжести. Тогда частота вращения окружности будет равна .

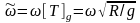Эту безразмерную частоту мы будем продолжать обозначать ω.

Перейдя в указанные масштабы, запишем и посчитаем все основные характеристики нашей частицы.

Потенциальная энергия U(φ) = - cosφ – (ω²sin²φ)/2.

Момент сил – dU/dφ = - sinφ(1 – ω²cosφ) и уравнение движения .

Условие равновесия dU/dφ = 0 выполняется в точках φ₁ = 0; φ₂ = π при любых значениях параметра ω и в точках cosφ_3,4 = 1/ω² при ω > ω_cr = 1. Значения потенциальной энергии в этих точках равны соответственно U(φ_1,2) = ±1 и U(φ_3,4) = - 1/2(1/ω² + ω²). Из физических соображений следует, что при медленном вращении, в нижней части окружности должен быть минимум, а в верхней - максимум потенциальной энергии.

При быстром вращении, в нижней точке, находящейся на оси окружности, должен существовать максимум, а в точках φ_3,4 должны быть симметрично расположенные относительно оси вращения минимумы. Так выглядит потенциальная энергия при двух значениях параметра ω.

Закон движения имеет вид

.

Точки остановки φ_min,max, то есть корни уравнения

E = U(φ) = - cosφ – (ω²sin²φ)/2

имеют место лишь при достаточно низких энергиях E < 1. При этих энергиях движение носит характер колебаний с периодом

.

При энергиях, больших единицы (mgl в произвольном масштабе), движение носит характер неравномерного вращения.

Так выглядит зависимость периода нелинейных колебаний от полной энергии при двух значениях параметра ω

Вблизи минимумов потенциальной энергии наблюдаются гармонические колебания, квадраты безразмерных частот которых равны второй производной потенциальной энергии U”(φ) = cosφ – ω²cos2φ в соответствующих точках устойчивого равновесия. При медленном вращении, то есть ω < ω_cr = 1, имеем

.

При быстром вращении 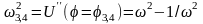. Найдите выражения для этих частот в произвольном масштабе.

Для более подробного изучения характеристик движения в данной задаче отсылаю Вас к интерактивному приложению,

Самостоятельно

• определите функцию Гамильтона системы;

• запишите канонические уравнения движения;

• запишите уравнение Гамильтона-Якоби;

• найдите его полный интеграл;

• найдите закон движения, используя полный интеграл уравнения Гамильтона-Якоби.

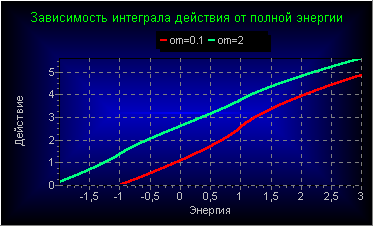
Как и в предыдущих задачах можно перейти в фазовом пространстве к каноническим переменным. Вот так выглядит зависимость действия J(E) от энергии в этой задаче при двух значениях параметра ω