Модуль 2. Конкурирующие взаимодействия

Интерактивное приложение, используемое в модуле

Задачи 10-19 (новая версия для OS Vista)

Примечание. Смысл приложения связан с контекстом излагаемой ниже теории.

Рассмотрим 10 простых задач классической механики, в которых участвует больше одного взаимодействия. В этих случаях уравнения движения будут содержать безразмерные параметры, определяющие относительную роль каждого из взаимодействий¹. Связано это с тем, что каждое из взаимодействий вносит свой масштаб времени в ускорение. Отношение этих масштабов и будет безразмерным параметром, от значения которого существенно зависит движение системы.

10. Гармонический осциллятор в среде с линейной вязкостью («Механика», §25).

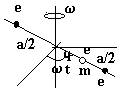
10. Заряженная частица m, e на равномерно вращающемся вокруг вертикальной оси стержне в поле двух таких же по величине и знаку зарядов, закрепленных на стержне симметрично относительно оси вращения на расстоянии a/2 от нее.

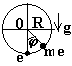
10. Заряженная частица m, e на вертикальной окружности радиуса R в поле закрепленного в нижней точке окружности того же по величине и знаку заряда и в поле тяжести g.

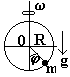
10. Частица m на вертикальной окружности радиуса R, равномерно вращающейся с угловой частотой ω вокруг вертикальной оси, проходящей через ее центр, в поле тяжести g.

10. Гармонический осциллятор в поле вынуждающей гармонической силы.

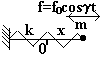
10. Гармонический осциллятор в поле вынуждающей гармонической силы и в среде с линейной вязкостью.

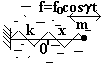
10. Частица m в бесконечно глубокой потенциальной яме с медленно движущейся стенкой (адиабатический процесс, «Механика», §49).

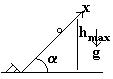
10. Частица на наклонной плоскости с медленно меняющимся углом наклона. Найти зависимость высоты подъема от угла наклона, используя адиабатический инвариант.

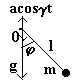
10. Плоский математический маятник с вертикально колеблющейся точкой подвеса («Механика», гл.1, зад.3 в), §30, зад. 1 к §30).

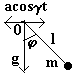
10. Плоский математический маятник с горизонтально колеблющейся точкой подвеса («Механика», гл.1, зад.3 б), §30, зад. 2 к §30).

В заключение модуля даются обобщения и комментарии.

10. Гармонический осциллятор в среде с линейной вязкостью

Эта система является фактически комбинацией систем 2 и 6 из модуля 1. Такая система совершает затухающие колебания.

Система диссипативная. Уравнения движения следуют из второго закона Ньютона. Действуют две конкурирующие силы – сила трения, линейно зависящая от скорости и возвращающая упругая сила

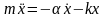
Выберем эталон массы [M] = m, то есть безразмерная масса равна . В задаче есть два масштаба времени. Один масштаб определяется упругим взаимодействием. Он равен масштабу времени задачи о гармоническом осцилляторе (задача 6 из модуля 1) 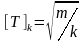. Другой масштаб времени определяется взаимодействием со средой как в задаче о движении частицы в среде (задача 2 из модуля 1). Этот масштаб равен [T]_ = m/. Любой из этих масштабов можно выбрать за эталон – единицу измерения времени в нашей задаче. Для определенности выберем в качестве эталона времени масштаб гармонического осциллятора [T]_k. В этом масштабе времени 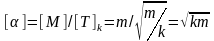, и коэффициент трения 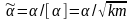. Обозначим эту безразмерную постоянную 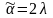, где λ - так называемый коэффициент затухания.

Таким образом, уравнение движения принимает вид

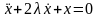(10.1)

Ищем решение этого уравнения в виде экспоненты x = e^rt. Подставляя эту функцию в уравнение (11.1), получим характеристическое уравнение r² + 2λr + 1 = 0, имеющее два корня 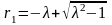и .

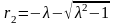Критическим значением коэффициента затухания является единица.