Апериодическое затухание
Если
λ > 1, то затухание
называется сильным, или апериодическим.
Общим решением уравнения движения
(11.1) является линейная комбинация двух
затухающих экспонент x
= Ae-(λ-d)t
+ Be-(λ+d)t,
где
.
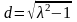При A = 0 затухание осуществляется по более «быстрой» экспоненте, с большим показателем λ + d. Этому закону движения x = Be-(λ+d)t; p = -B(λ + d)e-(λ+d)t отвечает прямая линия p = -(λ + d)x на фазовой плоскости.
При B = 0, решение отвечает более медленному затуханию x = Ae-(λ-d)t; p = -A(λ - d)e-(λ-d)t, а фазовая траектория представляет собой прямую линию p = -(λ - d)x с меньшим углом наклона.
Если ни A, ни B не равны нулю, то со временем быстро затухающее слагаемое x = Be-(λ+d)t становится пренебрежимо малым по сравнению с другим, медленно затухающим. Поэтому любое решение с неравными нулю A и B асимптотически приближается к решению с B = 0, а все фазовые кривые в конечном итоге попадают в ноль по прямой с меньшим углом наклона.
Здесь A и B – постоянные интегрирования, т. е. интегралы движения.
Интересно как выглядят уравнения движения затухающего осциллятора в канонических переменных w, J. Эти переменные, как мы помним из предыдущего модуля, значительно упростили запись уравнений движения обычного осциллятора (задача 6).
Связь
переменных «действие-угол» с обычными
фазовыми координатами x,
p
для свободного осциллятора имеет вид
J
= (x2
+ p2)/2;
tgw
= -p/x.
Такую же замену мы проведем и в наших
уравнениях для затухающего осциллятора
.
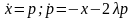Для этого продифференцируем по времени
записанные выше выражения для J
и w.
Получим,
.
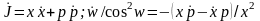Заменив
здесь
и
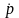правыми частями уравнений движения и
выразив затем x,
p
как функции J
и w,
получим уравнения движения затухающего
осциллятора в переменных «действие-угол»
.
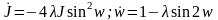Обратим внимание на то, что скорость изменения действия J отрицательная – фазовая точка стремится к началу фазовых координат. В случае > 1 скорость изменения угла обращается в ноль, когда угол достигает значения w, где sin2w = 1/. В этой же точке обращается в ноль и угловое ускорение (проверьте!). Поэтому угловая скорость в фазовом пространстве не меняет знак. Покажите самостоятельно, что эти предельные решения отвечают прямым линиям p = -( ± d)x (см. выше).
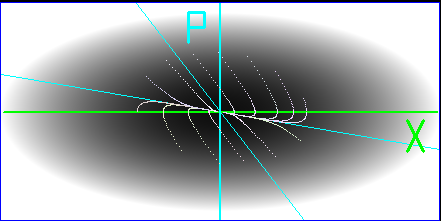
Пример фазового портрета при апериодическом затухании ( = 1.5)
Периодическое затухание
При слабом затухании λ < 1 закон движения имеет вид
,
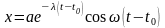где
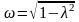- частота колебаний осциллятора. Это
так называемое периодическое затухание.
Фазовая траектория представляет собой
скручивающуюся спираль. Логарифм
отношения смещений через период T
= 2π/ω,
равный ln(x(0)/x(T))
= λT, называется
логарифмическим декрементом затухания.
Энергия затухающего гармонического
осциллятора (положим t0
= 0)
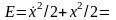
рассеивается в среднем по закону ‹E› = E0e-2λt, где E0 = a2/2 энергия осциллятора без затухания. Ведь средние значения косинуса и синуса за период равны нулю, а средние значения их квадратов равны ½
‹(-λcos(ωt) – ωsin(ωt))2 + cos2(ωt)› =
‹(1 + λ2)cos2(ωt) + λωsin(2ωt) +ω2sin2(ωt)› = 1
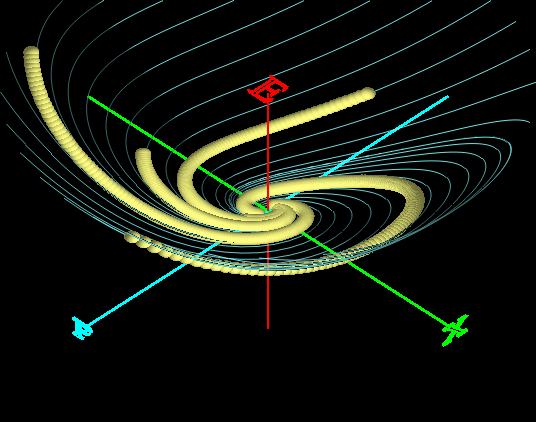
Периодическое затухание гармонического осциллятора в пространстве x, p, E (λ = 0.5)
Уравнение движения гармонического осциллятора в среде (10.1) инвариантно относительно сдвига времени, но энергия не сохраняется – она рассеивается в среду. В то же время у этого уравнения есть интеграл движения вида ½ (p2 + 2λ x p + x2) exp (2λ t) = const. Покажите это самостоятельно.
Посмотрите иллюстрацию движения гармонического осциллятора с затуханием. В начале, и при каждом новом значении безразмерного параметра, приложение накапливает фазовые траектории для дальнейшего их использования при построении фазового пространства в координатах x, p, E. Время накопления конечно, но для современных компьютеров почти не заметно. После накопления Вы сможете самостоятельно выбирать произвольные начальные условия и следить в динамике за развитием процесса в различных представлениях.