
- •Модуль 2. Конкурирующие взаимодействия
- •10. Гармонический осциллятор в среде с линейной вязкостью
- •Апериодическое затухание
- •Периодическое затухание
- •Выводы и комментарии
- •Вопросы для самоконтроля
- •11. Заряд на вращающемся стержне в поле двух других зарядов
- •Вопросы для самоконтроля
- •12. Заряд на окружности в поле тяжести
- •Вопросы для самоконтроля
- •13. Частица на вращающейся окружности в поле тяжести
- •Выводы и комментарии
- •Вопросы для самоконтроля
Выводы и комментарии
Каждому взаимодействию обычно соответствует свой масштаб времени.
В задаче об осцилляторе в среде есть масштаб времени осциллятора и масштаб времени воздействия среды [T] = m/.
От отношения масштабов времен существенно зависит характер движения.
В рассмотренной задаче безразмерное отношение
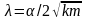 называется коэффициентом затухания.
называется коэффициентом затухания.При λ > 1 затухание осциллятора является апериодическим (сильное затухание), при λ < 1 – периодическим (слабое затухание).
Следует отметить, что не обязательно наличие двух взаимодействий приводит к появлению безразмерного параметра. Примером является движение в поле тяжести в вязкой среде (падение на парашюте). В этой задаче можно полностью избавиться от размерных параметров α, g, m выбором масштабов массы, длины, времени. Конкуренция двух взаимодействий сводится к их полному равновесию – парашют движется в пределе с постоянной скоростью, равной mg/α.
Вопросы для самоконтроля
Как выглядит уравнение движения гармонического осциллятора в среде?
Как использование масштабной инвариантности позволяет записать уравнение движения, и как выглядит общее решение (закон движения)?
Что представляет собой закон движения осциллятора в среде при сильном затухании, и как выглядят фазовые траектории в этом случае?
Каков закон движения гармонического осциллятора в среде при слабом затухании, каковы фазовые траектории?
Что такое логарифмический декремент затухания, и по какому закону в среднем рассеивается энергия гармонического осциллятора в среде?
11. Заряд на вращающемся стержне в поле двух других зарядов
Это лагранжева система. Найдем ее функцию Лагранжа.
В системе отсчета равномерно вращающегося стержня потенциальная энергия частицы складывается из центробежной энергии (см. задачу 5 модуля 1) Ucfg(q) = -mω2q2/2 и кулоновской энергии взаимодействия с закрепленными зарядами (задача 8 модуля 1)
UC = ke2/(a/2 – q) + ke2/(a/2 + q) = ke2a/(a2/4 – q2).
Поэтому функция Лагранжа имеет вид
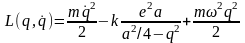 .
.
Выберем
масштаб массы
 ,
масштаб длины
,
масштаб длины
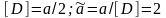 .
В задаче присутствуют два масштаба
времени. Один определяется частотой
вращения стержня и равен [T]
= 1/. Второй
масштаб времени связан с кулоновским
взаимодействием. Верна размерная формула
[ke2] = [M][D]3/[T]2.
Полагая в ней [ke2]
= ke2, имеем
кулоновский масштаб времени
.
В задаче присутствуют два масштаба
времени. Один определяется частотой
вращения стержня и равен [T]
= 1/. Второй
масштаб времени связан с кулоновским
взаимодействием. Верна размерная формула
[ke2] = [M][D]3/[T]2.
Полагая в ней [ke2]
= ke2, имеем
кулоновский масштаб времени
 .
Он порядка периода колебаний заряда на
покоящемся стержне. Для определенности
выберем в качестве эталона времени
масштаб вращения [T]
= 1/. В этом
масштабе времени безразмерный коэффициент
в кулоновской энергии равен ke2/[ke2]
= ke2/(m(a/2)3ω2).
Обозначим этот безразмерный коэффициент
просто буквой k. Тогда
потенциальная энергия, функция Лагранжа
и уравнение движения примут вид
.
Он порядка периода колебаний заряда на
покоящемся стержне. Для определенности
выберем в качестве эталона времени
масштаб вращения [T]
= 1/. В этом
масштабе времени безразмерный коэффициент
в кулоновской энергии равен ke2/[ke2]
= ke2/(m(a/2)3ω2).
Обозначим этот безразмерный коэффициент
просто буквой k. Тогда
потенциальная энергия, функция Лагранжа
и уравнение движения примут вид
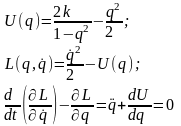
Здесь dU/dq = 4kq/(1 – q2)2 - q - сила с обратным знаком, действующая на частицу.
Движение частицы под действием двух конкурирующих сил – центробежной, равной q, и кулоновской –4kq/(1 – q2)2, существенно зависит от безразмерного коэффициента k. Исследуем поведение потенциальной энергии в зависимости от значения этого коэффициента.
Во-первых, ясно, что при всех ненулевых значениях k, то есть при наличии зарядов, потенциальная энергия образует потенциальные барьеры бесконечной высоты вблизи закрепленных зарядов - на границах интервала изменения координаты –1 < q < 1.
Во-вторых, потенциальная энергия имеет экстремальные значения внутри этого интервала. Координаты экстремальных точек потенциальной энергии можно найти, приравняв нулю ее первую производную
dU/dq = 4kq/(1 – q2)2 - q = 0.
Решая
это уравнение, получим один корень на
оси вращения q1
= 0, существующий при любых значениях k.
Два других, симметрично расположенных
относительно оси вращения корня
 ,
имеют место лишь при «слабом кулоне» k
< kcr
= 1/4.
,
имеют место лишь при «слабом кулоне» k
< kcr
= 1/4.
Физически ясно, что при достаточно малых значениях k центробежное отталкивание от оси вращения должно приводить к существованию максимума потенциальной энергии на оси вращения. В то же время, если влияние кулоновских сил отталкивания существенно, в симметричной точке q = 0 должен наблюдаться минимум потенциальной энергии. Найденное нами критическое значение kcr = 1/4 количественно определяет границу, отделяющую случай «слабого кулона» от «сильного кулона». Экстремальные точки q2,3, существующие при «слабом кулоне», очевидно, соответствуют минимумам потенциальной энергии.
Вот так выглядит потенциальная энергия при двух значениях параметра k.

Строго убедиться в характере экстремумов можно, посчитав вторые производные потенциальной энергии в экстремальных точках
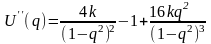 .
.
Имеем
U”(q = 0) = 4k - 1 (11.1)
 (11.2)
(11.2)
Из этих выражений ясно видно, что потенциальная энергия имеет минимум на оси вращения (вторая производная положительна) при условии k > kcr. При выполнении обратного неравенства в этой же точке находится максимум, в то время как в точках q = q2,3, расположены минимумы.
Значение потенциальной энергии на оси U(q = 0) = 2k, а в минимумах при «слабом кулоне» U(q = q2,3) = 2√k – 1/2.
Общее решение задачи о движении определяется из закона сохранения энергии, являющейся здесь первым интегралом движения
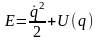 .
.
Отсюда
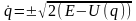 и
и
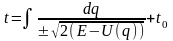 -
-
закон движения.
При не равном нулю коэффициенте k движение всегда финитно из-за отмеченных выше потенциальных кулоновских барьеров вблизи закрепленных зарядов. Период этого финитного движения определяется удвоенным временем прохождения между двумя точками остановки qmin, qmax, в которых полная энергия равна потенциальной
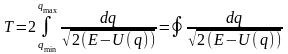 . (11.3)
. (11.3)
Это период нелинейных колебаний, которые могут иметь место, как в «большой яме», так и в двух симметричных «малых ямах», образующихся при «слабом кулоне». Вот как зависят периоды нелинейных колебаний от энергии при двух значениях безразмерного параметра k.
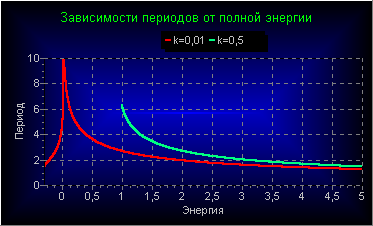
В непосредственной близости от дна любой из ям, то есть при малых энергиях, колебания становятся гармоническими. Квадраты соответствующих безразмерных частот гармонических колебаний равны вторым производным потенциальной энергии в минимумах ям, то есть определяются формулами (11.1) и (11.2). В том, что квадрат частоты малых колебаний ω0 определяется значением второй производной в минимуме потенциальной энергии, можно убедиться, если разложить потенциальную энергию в ряд вблизи минимума q = q0
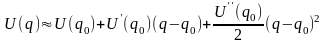 .
.
Первая производная в минимуме равна нулю, а постоянное слагаемое U(q0) не дает вклада в силу и, тем самым, в уравнение движения. Поэтому оставшееся слагаемое, квадратичное по отклонению от положения равновесия, имеет такой же вид, как потенциальная энергия частицы на пружинке с коэффициентом жесткости, равным U”(q0), или одномерного осциллятора из задачи 6 модуля 1. В выбранном масштабе с безразмерной массой, равной единице, коэффициент жесткости равен просто квадрату частоты гармонических колебаний.
Доказательство можно получить и непосредственно. Подставив разложение потенциальной энергии в выражение (11.3) для периода колебаний, получим интеграл вида

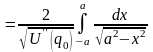
Здесь
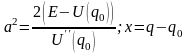 .
Табличный интеграл в правой части равен
π. Отсюда частота малых
колебаний
.
Табличный интеграл в правой части равен
π. Отсюда частота малых
колебаний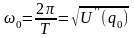 .
.
Имея безразмерные значения (11.1), (11.2) квадратов частот гармонических колебаний, найдите самостоятельно эти частоты в произвольном масштабе.
Иллюстрацию решения задачи 11 можно посмотреть, вызвав приложение.
Запишем
функцию Гамильтона и канонические
уравнения движения заряда. По определению,
функция Гамильтона связана с функцией
Лагранжа соотношением
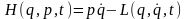 .
Независимыми аргументами функции
Гамильтона являются координата, импульс
и, в случае нестационарной системы,
время. Это параметры состояния механической
системы, или координаты точек в фазовом
пространстве. Функция Лагранжа есть
также функция состояния, но вместо
импульса она зависит от скорости. Поэтому
в приведенном выражении для функции
Гамильтона скорость в правой части
должна быть выражена через импульс.
Такое выражение может быть получено из
определения обобщенного импульса
.
Независимыми аргументами функции
Гамильтона являются координата, импульс
и, в случае нестационарной системы,
время. Это параметры состояния механической
системы, или координаты точек в фазовом
пространстве. Функция Лагранжа есть
также функция состояния, но вместо
импульса она зависит от скорости. Поэтому
в приведенном выражении для функции
Гамильтона скорость в правой части
должна быть выражена через импульс.
Такое выражение может быть получено из
определения обобщенного импульса
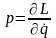 .
.
В нашей задаче
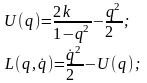
Поэтому
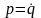 и, следовательно, H(q,
p) = p2/2
+ U(q).
Это очевидный результат. Ведь функция
Гамильтона есть энергия, в которой
скорость выражена через импульс.
и, следовательно, H(q,
p) = p2/2
+ U(q).
Это очевидный результат. Ведь функция
Гамильтона есть энергия, в которой
скорость выражена через импульс.
Уравнения движения в форме канонических уравнений имеют вид
 .
.
Подставим в них функцию Гамильтона нашей задачи
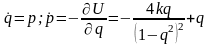 .
.
Так выглядят уравнения движения заряда на вращающемся стержне в кулоновском поле зарядов, закрепленных на концах стержня.
Наконец, сформулируем нашу задачу в терминах уравнения Гамильтона-Якоби.
Общий
вид уравнения Гамильтона-Якоби для
системы с одной степенью свободы
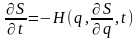 .
Здесь S = S(q,t)
неизвестная функция координаты и времени
– действие. В выражении для функции
Гамильтона, стоящем справа, импульс
заменен производной действия по
координате.
.
Здесь S = S(q,t)
неизвестная функция координаты и времени
– действие. В выражении для функции
Гамильтона, стоящем справа, импульс
заменен производной действия по
координате.
В нашей задаче, для которой мы только что записали функцию Гамильтона, уравнение Гамильтона-Якоби имеет вид

Конкретное выражение потенциальной энергии записано выше.
Дальнейшие рассуждения повторяют то, что было сказано в модуле 1.
Наша система является консервативной. Ее функция Гамильтона не зависит явно от времени. Поэтому зависимость функции S от двух переменных - координаты и времени, разделяется. Другими словами решение уравнения Гамильтона-Якоби можно искать в виде суммы двух функций S(q,t) = S0(q) + S1(t). Каждая из функций-слагаемых зависит только от одной переменной – координаты или времени.
Подставим такое представление решения в уравнение Гамильтона-Якоби
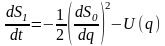 .
.
Мы заменили частные производные обычными, так как каждая из функций S0 и S1 зависит только от одного аргумента.
Мы предполагаем, что подставленная в уравнение функция S = S0 + S1 является решением. Поэтому правая и левая части равенства должны быть тождественно равны друг другу при любых значениях независимых аргументов q и t. Но в нашем случае левая часть не содержит координаты, а лишь время. Правая часть – наоборот. Равенство между ними возможно, лишь, если обе эти части не будут зависеть ни от координаты, ни от времени. Другими словами, обе части соотношения должны быть постоянными.
Функция Гамильтона имеет смысл энергии. Энергия со знаком минус и является постоянной, которой равна левая часть dS1/dt = -E и правая часть
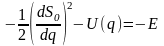 .
.
Из первого соотношения находим ту часть действия, которая зависит только от времени
S1(t) = - Et + const. (11.4)
Из второго соотношения находим ту часть действия, которая зависит только от координаты (укороченное действие):
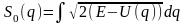 . (11.5)
. (11.5)
Отметим сразу, что не зависимо от числа степеней свободы и конкретного выражения функции Гамильтона в действии консервативной системы зависимость от времени всегда отделяется и имеет вид (11.4).
Полное действие, то есть полный интеграл уравнения Гамильтона-Якоби консервативной одномерной системы вообще и нашей задачи в частности имеет вид
S(q,t) = S0(q,E) - Et + const.
Это решение содержит две независимых постоянных E и const. Постоянная const аддитивна и в дальнейшем не существенна. Зависимость от энергии важна. Дифференцируя найденный полный интеграл уравнения Гамильтона-Якоби по энергии, и приравнивая результат новой постоянной, получим закон движения
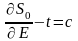 .
.
Постоянная c имеет смысл начального момента времени t0, взятого с обратным знаком. Взяв производную по параметру E, от которого зависит интеграл (11.5) для S0, получим закон движения консервативной одномерной системы в уже знакомом нам виде:
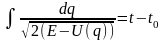 .
.
Особенно просто выглядит полный интеграл уравнения Гамильтона-Якоби в переменных «действие-угол». Как и в задачах 6-8 S(w,t) = Jw – Et. Здесь
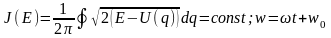
Частота равномерного вращения ω = 2π/T угловой координаты w определяется рассмотренным выше (11.3) периодом нелинейных колебаний T, зависящим от энергии. А вот так зависит от энергии интеграл действия при двух значениях параметра задачи.
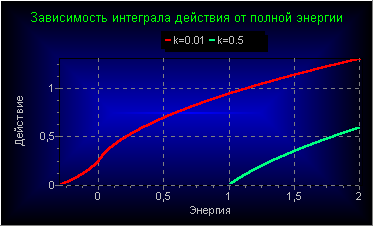
Заметим, что при тех энергиях, где имелось два несвязанных контура интегрирования (колебания в «малых ямах»), в расчет изображенной зависимости J(E) принималась сумма действий по обоим контурам.
