Вопросы для самоконтроля

1. Запишите функцию Лагранжа задачи 11 в общем, и безразмерном виде. Поясните роль и физический смысл безразмерного параметра.

2. Запишите уравнение движения задачи 11, следующее из уравнения Лагранжа.

3. Проведите полный анализ потенциальной энергии в задаче 11. Поясните характер движения при различных значениях безразмерного параметра и различных начальных условиях. Какой физический смысл имеет критическое значение безразмерного параметра?

4. Как выглядят фазовые портреты задачи 11 при k < k_cr и k > k_cr?

5. Как определяется период нелинейных колебаний?

6. Определите частоты гармонических колебаний задачи 11 вблизи устойчивых положений равновесия при различных значениях безразмерного параметра.

7. Запишите функцию Гамильтона и уравнения движения в форме канонических уравнений задачи 11.

8. Запишите и решите уравнение Гамильтона-Якоби задачи 11, получив полный интеграл и закон движения. Как выглядит закон движения в канонических переменных?

12. Заряд на окружности в поле тяжести

Это сочетание взаимодействий, определяющих движение плоского математического маятника (задача 7 модуля 1) и частицы в кулоновском поле (задача 8).

Функция Лагранжа системы имеет, следовательно, вид

.

Выбор масштабов длины и массы очевиден

.

Но, как и в предыдущих задачах, мы имеем два масштаба времени. Один определяется кулоновским взаимодействием как в задаче 8 модуля 1. Этот масштаб порядка периода колебаний заряда при отсутствии поля тяжести. Второй масштаб времени связан с полем тяжести. Он порядка периода колебаний тяжелого маятника (задача 7 модуля 1). Для определенности в качестве единицы выберем масштаб кулоновского взаимодействия [T]_C. В этом случае безразмерное значение ускорения свободного падения равно

.

Мы по-прежнему будем обозначать этот параметр g.

Исследуем поведение потенциальной энергии при различных значениях g.

Имеем . На границах интервала 0 < φ < 2π, как и в предыдущей задаче, существует бесконечно высокий кулоновский барьер, отталкивающий частицу от закрепленного заряда. Физически ясно, что при малых значениях безразмерного g в симметричной точке φ = π должен быть минимум потенциальной энергии – устойчивое положение равновесия. Но при «слабом кулоне», или «сильной тяжести», то есть при больших значениях коэффициента g, устойчивость у симметричного положения равновесия должна отсутствовать.

Подставив функцию Лагранжа 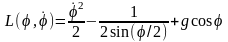в уравнение Лагранжа, получим уравнение движения частицы в поле двух сил. В точках, где полный момент сил

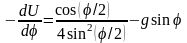
равен нулю, находятся положения равновесия. Представляя второе слагаемое в виде gsinφ = 2gsin(φ/2)cos(φ/2), получим один корень cos(φ₁/2) = 0: φ₁ = π, существующий при любом значении параметра g, и два симметрично расположенных положения равновесия , имеющих место лишь при условии достаточно «сильной тяжести» g > g_cr = 1/8.

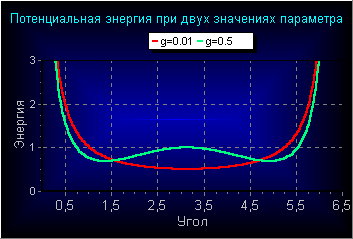
Вот как выглядит потенциальная энергия при двух значениях параметра g.

Закон движения, как и в предыдущей задаче, следует из закона сохранения полной энергии – первого интеграла уравнения движения

.

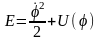Отсюда и закон движения

.

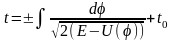Движение финитно при любых значениях безразмерного параметра g, и его период определяется аналогичной формулой

,

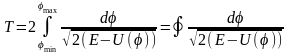где пределы интегрирования φ_min,max являются точками остановки, то есть корнями уравнения E = U(φ).

Так выглядит зависимость периода нелинейных колебаний от полной энергии при двух значениях безразмерного параметра g.

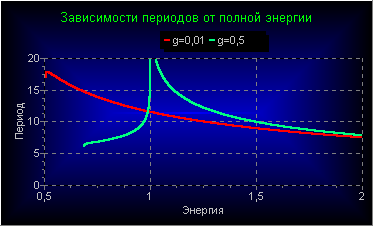
При «слабой тяжести», то есть при g < g_cr = 1/8, в верхней точке окружности потенциальная энергия имеет минимум и значение в нем U(φ = π) = ½ + g. При полных энергиях, близких к этому значению, частица совершает малые гармонические колебания, квадрат частоты которых равен .

Вторая производная потенциальной энергии равна

.

Поэтому .

При «сильной тяжести» верхнее положение равновесия становится неустойчивым. Но имеются два других устойчивых положения равновесия, расположенных симметрично относительно вертикальной оси в точках

.

Значение потенциальной энергии в этих точках равно . Если полная энергия близка к этому значению, то частица совершает гармоническое колебание в той или иной потенциальной яме с частотой, квадрат которой равен

.

Запишите найденные частоты в произвольном масштабе.

Посмотрите графическую иллюстрацию исследованного движения. Проверьте численное соответствие полученных формул и результатов расчетов при малых колебаниях.

Самостоятельно

• определите функцию Гамильтона системы;

• запишите канонические уравнения движения;

• запишите уравнение Гамильтона-Якоби;

• найдите его полный интеграл;

• найдите закон движения, используя полный интеграл уравнения Гамильтона-Якоби.

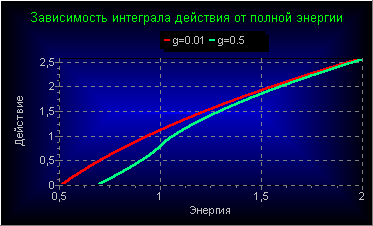
Так как движение финитное, то, как и в предыдущей задаче, можно перейти от фазовых координат , p_ к каноническим переменным w, J. Вот так выглядит зависимость действия J(E) от энергии в этой задаче при двух значениях безразмерного параметра g.