2. Учет инфляции при расчете наращенных сумм

Инфляционные процессы уменьшают реальную стоимость денег.

Ставку, скорректированную (увеличенную) на инфляцию, условно можно называть брутто-ставкой.

Ведем следующие обозначения:

– номинальная ссуда с процентами;

– реальная ссуда с процентами, т.е. покупательная способность S_н;

r – реальная процентная ставка ( реальная простая процентная ставка, реальная простая сложная ставка);

брутто-ставка;

- темп инфляции (темп прироста цен), в процентах;

– расчетный период (срок) в годах;

- годовой индекс цен, в разах.

С учетом принятых обозначений, годовые формулы наращения примут вид:

Последнюю формулу нужно понимать так: ссуда за год реально выросла по ставке и за счет инфляции по темпу инфляции . Вместо подставим ее значение:

или

Произведя преобразования, получим:

1. 

Данное выражение известно, как формула И.Фишера, в которой (α+rα) является величиной, которую необходимо прибавить к реальной ставке доходности для компенсации инфляционных потерь.

2. 

Это точная формула расчета реальной ставки процента по известным величинам номинальной ставки процента и темпу инфляции. При низких темпах инфляции применяют приближенную формулу . При значительной инфляции нужно применять точную формулу.

Также брутто-ставку можно рассчитать через индекс цен.

Темп инфляции определяется как: ,

Индекс цен рассчитывается:

1. Простые брутто-ставки:

- простая процентная брутто-ставка : ;

- простая учетная брутто-ставка : .

2. Сложные брутто-ставки:

- сложная процентная брутто-ставка :

- сложная учетная брутто-ставка : ;

- сложная номинальная процентная брутто-ставка : _.

- сложная номинальная учетная брутто-ставка :

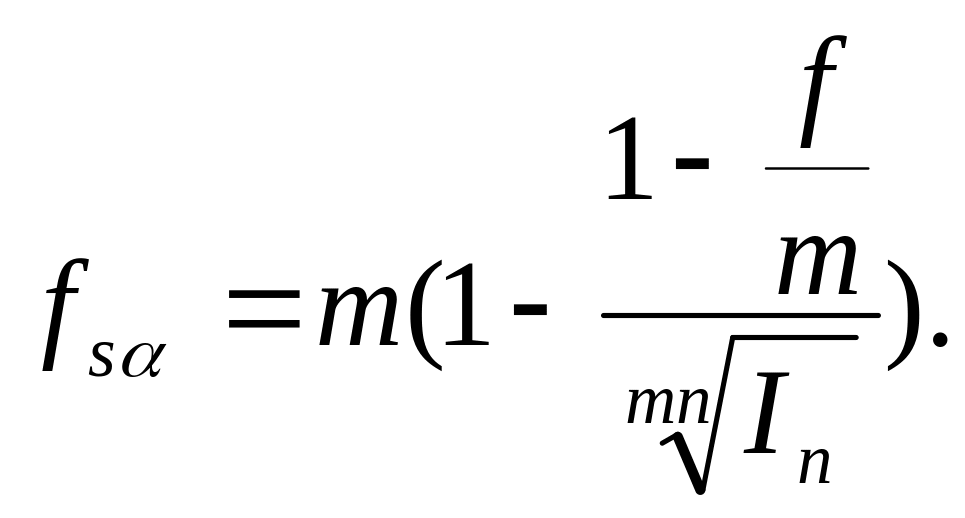
Пример 1.

Первоначальный капитал в размере 20000 руб. выдается на 3 года, проценты начисляются в конце каждого года по ставке 8% годовых. Определите наращенную сумму с учетом инфляции, если ожидаемый годовой уровень инфляции составляет 12%.

Решение.

По условию задачи .

1. Для определения индекса инфляции воспользуемся формулой:

2. Определим наращенную сумму:

Пример 2.

При выдаче кредита в сумме 40 млн. руб. должна быть обеспечена реальная доходность операции, определяемая простой процентной ставкой 14% годовых. Кредит выдается на полгода, индекс инфляции составит 1,06. Рассчитать значение процентной ставки, компенсирующей потери от инфляции, и наращенную сумму.

Решение.

По условию задачи:

1. По формуле определим процентную ставку, компенсирующую потери от инфляции:

2. По формуле определим наращенную сумму:

3. Наращенную сумму можно определить и по формуле:

Результаты определения наращенной суммы совпадают.

Пример 3.

Кредит в 1,5 млн. руб. выдан на 2 года. Реальная доходность должна составлять 11% годовых (сложные проценты). Расчетный уровень инфляции 16% в год. Определить ставку процентов при выдаче кредита, а также наращенную сумму.

Решение.

2. 

Задачи для самостоятельного решения.

Задача 1. Определить реальную ставку простых процентов за год, если брутто-ставка равна 10 % при годовой инфляции 7 %.

Задача 2. На сумму в 10 тыс. руб. в течение трех месяцев начислялись простые проценты по ставке 10 % годовых. За каждый месяц цены росли соответственно на 10, 15 и 20 %. Найти наращенную сумму с учетом инфляции и величину положительной процентной ставки.

Задача 3. На вклад в 100 тыс. руб. ежемесячно начисляются сложные проценты по номинальной годовой процентной ставке 8 %. Оценить сумму вклада через 1,5 года с точки зрения покупательной способности, если ожидаемый темп инфляции 2 % в месяц. Какова должна быть величина положительной процентной ставки?