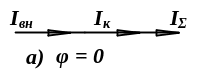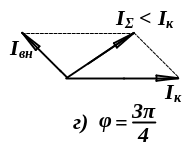1.2. Основные принципы получения незатухающих колебаний

Для получения незатухающих электромагнитных колебаний необходимо пополнять энергию в контуре на величину потерь за один период колебания . Это пополнение энергии должно осуществляться в каждый период.

Пополнение энергии можно осуществлять через период, через два и т.д. периода, но при этом должны быть скомпенсированы потери энергии соответственно за два, три и т.д. периода колебаний.

Используя выражение для контурного тока (1.4), получим энергию потерь за период

;

за два периода

;

за три периода

;

и т.д.,

где ;

U₀ – напряжение на конденсаторе или катушке индуктивности в момент времени t = 0 (см. рис. 1.2,б).

Общее выражение потерь энергии за n-периодов колебаний имеет следующий вид:

. (1.13)

Выражение (1.13) имеет важное значение для построения умножителей частоты сигнала, используемых в генераторах электромагнитных колебаний.

Поступление энергии в колебательный контур должно осуществляться в нужную фазу. Так как носителем энергии является ток, то он должен быть вызван внешним источником энергии и протекать в фазе с контурным током.

Рассмотрим возможные фазовые соотношения между векторами – контурного тока и – тока от внешнего источника на фазовой плоскости (рис. 1.3). При фазовом сдвиге между векторами модуль суммарного вектора тока и ток от внешнего источника I_вн не может компенсировать потери энергии в контуре.

Рис. 1.3. Векторные диаграммы токов: а – фазовый сдвиг между векторами и равен нулю, суммарный вектор тока имеет максимальное значение модуля; б – фазовый сдвиг ; в – фазовый сдвиг , при этом ; г – фазовый сдвиг , например ,

Если же фазовый сдвиг , то модуль суммарного вектора и колебания в контуре будут затухать быстрее. В этом случае энергия внешнего источника будет расходоваться на гашение колебаний в контуре.

Выводы:

1. Для получения незатухающих колебаний в контуре необходимо пополнять энергию в контур на величину потерь. При этом под потерями следует понимать собственные потери в колебательном контуре, определяемые выражением (1.13), а также ту часть колебательной энергии, которую контур отдает в нагрузку.

2. Пополнение энергии должно осуществляться от внешнего источника энергии посредством тока. При синфазности тока от внешнего источника энергии i_вн(t) и контурного тока i_к(t) расход энергии внешнего источника на покрытие потерь в контуре будет минимальным. При увеличении фазового сдвига между этими токами суммарный вектор будет уменьшаться. Для того, чтобы скомпенсировать потери энергии в контуре при необходимо увеличивать ток от внешнего источника I_вн, то есть увеличивать расход энергии.

3. При фазовом сдвиге и I_вн < I_к процесс затуханий в колебательном контуре идет быстрее. В этом случае энергия внешнего источника расходуется на подавление колебаний.

4. В том случае, когда I_вн >> I_к, то собственными колебательными процессами в контуре можно пренебречь и рассматривать контур как r, L, C – цепь. на которую воздействует эдс (см [1], п. 4-4. Установившийся синусоидальный ток в цепи с последовательным соединением участков r, L, и C; п. 4-5. Установившийся синусоидальный ток в цепи с параллельным соединением участков g, L, и C; п. 4-6. Активная, реактивная и полная мощности; п.4-7. Мгновенная мощность и колебательная энергия в цепи синусоидального тока.).