Линейно разделимые сигналы.

Рассмотрим МС в которой групповой сигнал представляет собой сумму канальных сигналов. Разделяющее устройство является линейным 4-хполюстников, а канальные сигналы являются линейно разделимыми. При этом помехи и искажения отсутствуют.

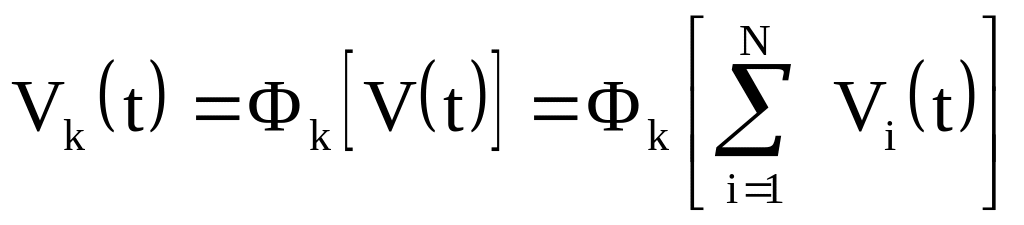, (1).

, (2).

, (3).

Множество канальных сигналов называются линейно разделимыми, если выражение (3) является справедливым для всех канальных сигналов каждого из этих множеств.

Существует теорема: для того, чтобы канальные сигналы были линейно разделимыми, необходимо и достаточно, чтобы эти множества были линейными и не имели взаимных пересечений.

Линейное множество – это множество, которому принадлежит не только сами элементы, но и их линейная комбинация.

, .

Канальные сигналы или функции … являются линейно независимыми, если их линейная комбинация равна при условии, что козфф-ты равны нулю.

Рассмотрим ряд функций, которые являются линейно независимыми и которые используются в качестве канальных сигналов.

V(t) = A₁

А₁

A₀+ A₁t

V(t) V₁(t) = A₀

В принципе к линейно разделимым сигналам относят множество сигналов, частотные спектры которых не содержат гармонических составляющих выше некоторой верхней частоты, следовательно и линейная комбинация таких сигналов не будет содержать число превышающих .

Формирование канальных сигналов.

Для разделения канальных сигналов должно выполняться условие их линейной независимости. Необходимо, чтобы в канальных сигналах отображались первичные сообщения без информационных потерь. Для выполнения этих условий выбирают из некоторого множества R класс линейно независимых функций.

Необходимо, чтобы эти функции формировались спец. генератором с фиксированными параметрами. Эти функции называются переносчиками, а величины представляют собой постоянные параметры переносчиков.

Модуляция этих функций переносчиков осуществляется первичными сообщениями. Переносчики являются линейно независимыми, их можно выделить из суммы канальных сигналов линейным разделяющим устройством и как следствие использовать в качестве канальных сигналов.

Сущность модуляции состоит в том, что 1 или несколько параметров изменяются пропорционально первичному сигналу, в результате имеем модулированное колебание.

Если в качестве модулированного параметра использовать , то можно записать

выражение, отражающее изменение модулированного параметра:

- величина модулированного параметра при отсутствии модуляции.

- девиация модулированного параметра.

- нормированное значение модулирующего первичного сигнала.

- глубина модуляции.

Лекция 6 Характеристика переносчиков и синтез разделяющих устройств

Переносчики классифицируются 2-мя типами параметров:

1. информационные параметры ( те, которые подвергаются модуляции в процессе взаимодействия с первичным сигналом).

2. разделительные параметры.

С₁(t) V₁(t)

- информационный параметр,

C₂(t) V₂(t) - разделительный параметр, который определяет

принадлежность i-го канального сигнала,

В случае модулятора используется

перемножитель.

,

- период переносчика.

C_n(t) V_n(t)

При

Выполняется следующее условие: при величина =const. Поэтому сигналы различных каналов отличаются др. от друга разделительного параметра .

Переносчики разделяют следующим образом:

1. гармонические (АМ, ЧМ, ФМ)

2. прямо периодические последовательности прямоугольных импульсов (АИМ, ШИМ, ВИМ, ЧИМ, ФИМ)

3. кодовые последовательности в виде многопозиционных сигналов (функции Уолша, Лагери, Якоби, Лежандра).

Для каждого вида переносчиков характерны способы разделения:

1. разделение по

2. по времени

3. по форме сигнала.