Лекция 3. Условная энтропия дискретного источника. Ортогональные представления сигналов.

В большинстве случаев для передачи сигнала рассматривают симметричный канал связи с помехами:

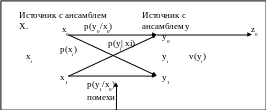
Ансамбль x – набор возможных реализаций , которыми обладает источник.

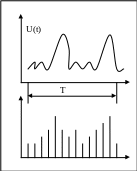U(t) – случайный процесс, за интервал Т мы можем наблюдать множество реализаций, наблюдать разные реализации этого случайного процесса. Также существует множество интервалов Т. Следовательно, существует ансамбль реализаций.

0101011 → через канал связи => p(y_j)

H(X,Y) – энтропия обеих (совместных) источников, вероятность совместного события:

p(x_i , y_j ) = p(x_i)·p(y_j)

Случай взаимозависимых событий (состояний наших источников) нас интересует, какова условная энтропия H(X,Y) ансамбля X по отношению к ансамблю источника Y:

Н(Х/Y=y_i ) - эта условная энтропия отражает случайную величину, характеризующую неопределенность, приходящуюся на одно состояние ансамбля Х при условии, что реализовалось одно конкретное значение (состояние) величины у_i из ансамбля Y (данную величину называют частной условной энтропией ансамбля Х)

При переходе к взаимозависимым событиям, возникающих из-за наличия помех в канале, совместная вероятность такого события будет:

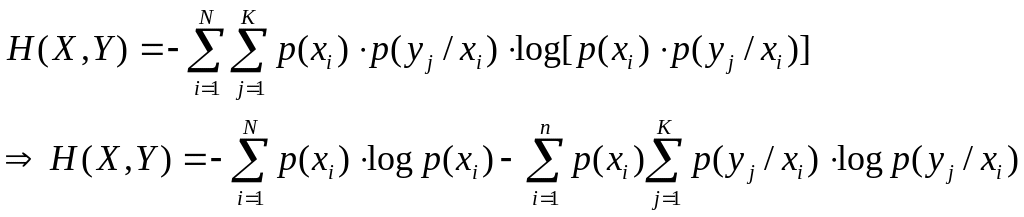
Выражение для условной энтропии можно привести к более компактному виду, если усреднить ее по всем возможным состояниям (ансамблям) :

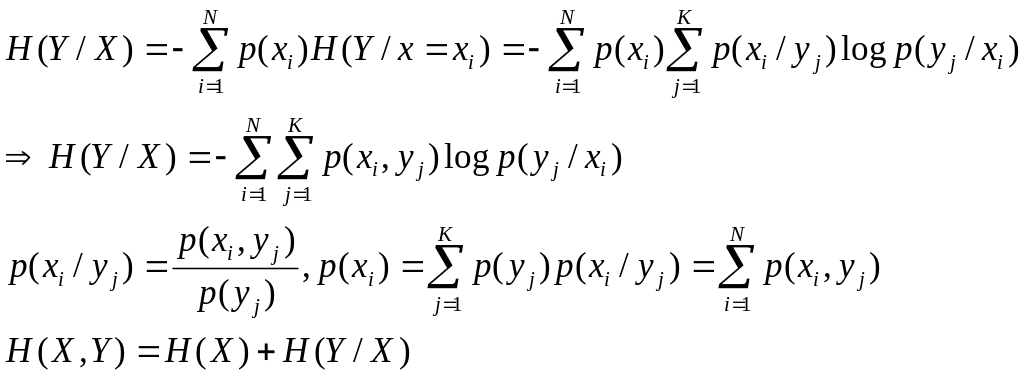
Ортогональное представление сигналов.

В радиотехнике существуют различные математические модели сигналов и помех, среди которых различают:

1. Детерминированные

2. Квазидетерминированные

3. Случайные модели сигналов

Квазидетерминированные – какой-то из известных параметров может измениться (уйти). Например, фаза.

В телекоммуникациях всегда стараются найти такую форму представления сигнала, несущего информацию, которая облегчала бы его прохождение через радиотехническую систему.

С этой целью сложные сигналы представляют совокупность базисных (линейно независимых) функций φ_k(t):

- обобщенный ряд Фурье

,где Т – интервал наблюдения.

При выбранном наборе базисных функций φ_k(t) исходный сигнал U(t) полностью определяется совокупностью безразмерных коэффициентов С_к. Совокупность чисел С_k образуют дискретный спектр сигнала.

Суть представления любого сигнала через преобразование Фурье состоит в следующем:

с помощью рядов Фурье практически любой сигнал можно представить в виде ряда гармонических сигналов, например синусоидальных. Набор этих синусных функций формирует так называемые спектральные составляющие сигнала и, как следствие, наше представление об исходном процессе U(t) будет формироваться уже в частотной области:

- экспоненциальная форма представления сигнала

- чем больше составляющих, тем выше точность.

На интервале наблюдения Т выражение справедливо как для сигналов конечной длительностью, так и для сигналов, неограниченных во времени. В общем случае, за пределами интервала наблюдения сигнал, конечно же не равен нулю, но при этом он считается периодически повторяющимся.

Поскольку частотный спектр отображает распределение частотных компонентов и соответствующих амплитуд, выражение можно записать и для определения сигнала в любой момент времени:

, где

S(ω) – спектральная плотность мощности

φ(ω, t) – базисная функция с непрерывно изменяющимся параметром ω. В этом случае сигнал в частотной области представляется в виде сплошного спектра.

Базисные функции выбирают такими, чтобы они имели простое аналитическое выражение, обеспечивали бы быструю сходимость ряда, имели простую техническую реализацию.

Спектральная плотность мощности наблюдаемого процесса характеризует распределение мощности отдельных спектральных компонент сигнала в частотной области.

Периодические сигналы

Если близко к единице, то сигнал называют узкополосным, если же , то сигнал называется широкополосным. Выполним преобразование выражения - ортогонализация представления сигнала. Для этого выбираем набор базисных функций φ_j(t). Обеспечиваем свертку исходного процесса с базисными функциями:

;

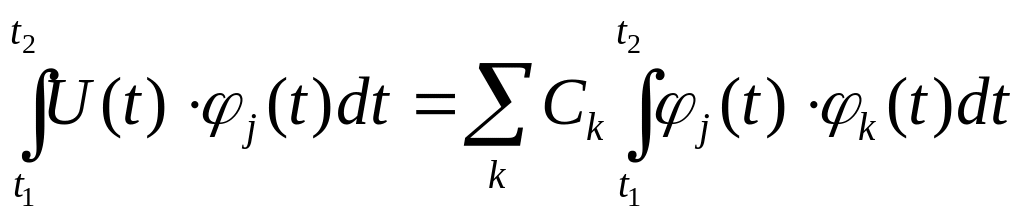Для функций, ортогональных на отрезке [t₁, t₂] выполняется следующее условие:

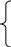
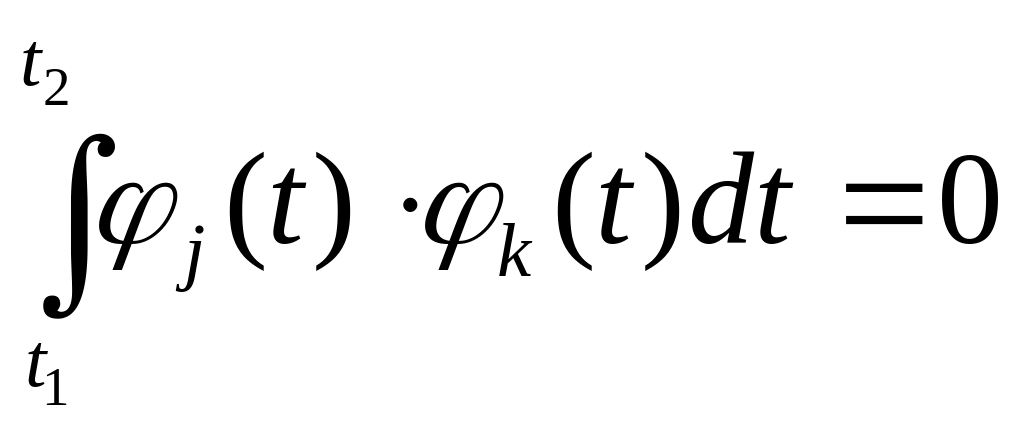, при j ≠ k =>

при k = j: .

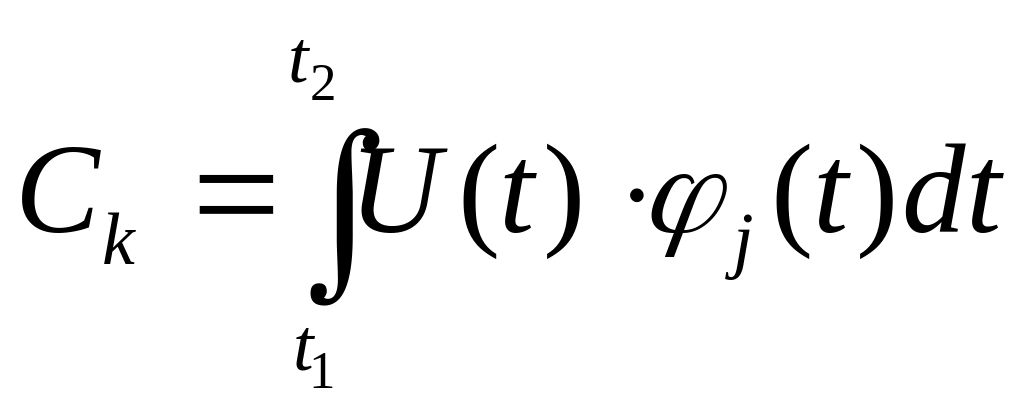Критерий среднеквадратической сходимости ряда и исходной функции U(t):

.

Вводим условие нормировки, которому удовлетворяет система ортогональных функций на заданном интервале. Когда k = j все интегралы = 1.

δ – среднеквадратическая сходимость исходного ряда и нашей функции.