
- •Оглавление Введение 4 Программа курса по теории функций комплексной переменной 5
- •Контрольные работы 63 Библиографический список 83
- •Программа курса по теории функций комплексной переменной
- •Глава 1. Методические указания к программе
- •Глава 2. Комплексные числа
- •Примеры
- •Глава 3. Конформные отображения
- •3.1. Дробно-линейная функция
- •Примеры
- •3.2. Показательная и тригонометрические функции комплексного аргумента
- •Примеры
- •3.3. Логарифмы комплексных чисел. Степень с действительным показателем
- •Примеры
- •Примеры
- •3.4. Функция Жуковского
- •Примеры
- •Примеры
- •24. Найти образы области :
- •3.5. Конформные отображения, определяемые комбинациями основных элементарных функций
- •Примеры
- •Глава 4. Интеграл от функции комплексной переменной
- •4.1. Понятие интеграла от функции комплексной переменной
- •Примеры
- •4.2. Интегральная теорема Коши
- •Примеры
- •4.3. Интегральная формула Коши
- •Примеры
- •Глава 5. Степенные ряды
- •5.1. Понятие степенного ряда Определение 9. Степенным рядом называется функциональный ряд вида
- •Примеры
- •5.2. Ряд Тейлора
- •Примеры
- •5.3. Ряд Лорана
- •Примеры
- •5.4. Классификация изолированных особых точек однозначного характера аналитической функции
- •Примеры
- •Глава 6. Вычеты
- •6.1. Вычисление вычетов
- •Примеры
- •6.2. Вычисление интегралов с помощью вычетов
- •Примеры
- •Примеры
- •Примеры
- •Контрольные работы Контрольная работа 1
- •Контрольная работа 2
- •Контрольная работа 3
- •410012, Саратов, Астраханская, 83. Типография Издательства Саратовского университета. 410012, Саратов, Астраханская, 83.
Примеры
26.
Вычислить
![]() ,
где
– часть окружности
,
,
где
– часть окружности
,
![]() ,
выбрав за начало
точку
.
,
выбрав за начало
точку
.
Решение.
Запишем уравнение кривой
в виде
![]() ,
,
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
Используя формулу (14), имеем:
.
Используя формулу (14), имеем:
![]() .
.
27.
Вычислить
![]() ,
где
– дуга параболы
,
где
– дуга параболы
![]() ,
,
![]() ,
,
![]() – начало кривой.
– начало кривой.
Решение. Выпишем действительную и мнимую части подинтегральной функции:
![]()
Воспользовавшись
формулой (15), имеем
![]()
![]()
![]() .
.
28.
Вычислить
![]() ,
где
– квадрат с вершинами в точках 1,
,
,
где
– квадрат с вершинами в точках 1,
,
![]() ,
,
![]() (рис. 9).
(рис. 9).
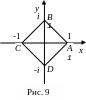 Решение.
Поскольку на сторонах квадрата ABCD
выполняется равенство |Re(z)|+|Im(z)|=|x|+|y|=1,
получаем
Решение.
Поскольку на сторонах квадрата ABCD
выполняется равенство |Re(z)|+|Im(z)|=|x|+|y|=1,
получаем
![]() .
.
Подсчитаем интеграл вдоль отрезка AB: y=1-x, 0x1, dy = – dx, Dz = dx + idy = (1– i)dx, откуда
![]()
Аналогично,
![]()
![]()
![]()
Окончательно,
![]()
4.2. Интегральная теорема Коши
ТЕОРЕМА
(Интегральная теорема Коши). Если функция
![]() – аналитическая в односвязной области
D,
то интеграл от нее по произвольному
замкнутому жордановому кусочно-гладкому
контуру L,
целиком лежащему в области D,
равен нулю:
– аналитическая в односвязной области
D,
то интеграл от нее по произвольному
замкнутому жордановому кусочно-гладкому
контуру L,
целиком лежащему в области D,
равен нулю:
![]() .
(16)
.
(16)
Из этой теоремы вытекает: а) если аналитична в области D, то интеграл не зависит от пути интегрирования, т.е. если 1 D и 2 D – две кривые, имеющие общие начало и конец, то
![]() ;
;
b)
если функции
и
![]() вместе со своими производными первого
порядка аналитические в односвязной
области D,
то справедлива формула
вместе со своими производными первого
порядка аналитические в односвязной
области D,
то справедлива формула
 ;
;
![]() ;
;
Примеры
29.
Определить, когда для интеграла
![]() можно применить интегральную теорему
Коши, если L:
можно применить интегральную теорему
Коши, если L:
a)
| z
| =![]() ;
b)
| z
-
|
=
;
b)
| z
-
|
=![]() ;
c)
| z
-
1|
= 4; d)
| z
| = 3.
;
c)
| z
-
1|
= 4; d)
| z
| = 3.
![]()
Решение.
Подинтегральная функция
Решение.
Подинтегральная функция
![]() имеет особенности в точках z
= ± 2,.
Следовательно,
имеет особенности в точках z
= ± 2,.
Следовательно,
a)
круг
![]() полностью входит в область аналитичности
и (16) имеет место;
полностью входит в область аналитичности
и (16) имеет место;
b) рассуждая аналогично п. а), имеем (16);
c) в круге с центром z = 1 и радиуса 4 функция имеет особенности и не является аналитической, следовательно, теорема Коши не применима;
d) рассуждая аналогично п. с), получаем, что теорема Коши также не применима.
3 0.
Доказать, что
0.
Доказать, что
![]() .
.
Решение.
Функция
![]() – аналитична на всей комплексной
плоскости. Проинтегрируем
по контуру прямоугольника
– аналитична на всей комплексной
плоскости. Проинтегрируем
по контуру прямоугольника
![]() ,
,
![]() (рис. 10). Из (16) следует, что
(рис. 10). Из (16) следует, что
![]() .
Тогда
.
Тогда


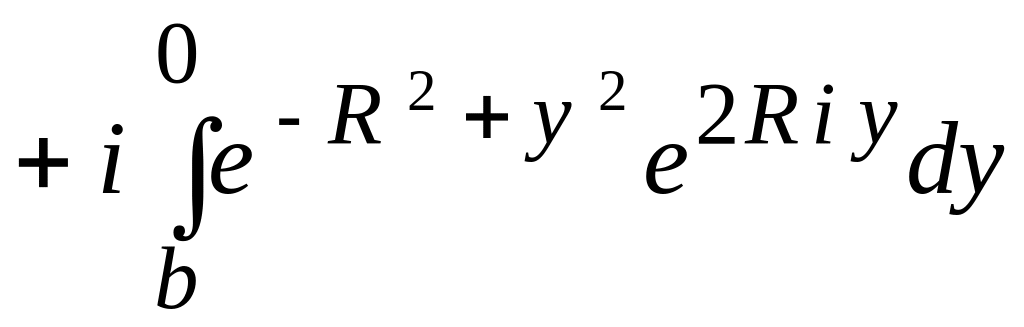 .
.
Если объединить второй и четвертый интегралы, разбить третий интеграл на два и воспользоваться формулами Эйлера
![]() ,
,
![]() ),
),
то полученную сумму интегралов можно будет записать в виде
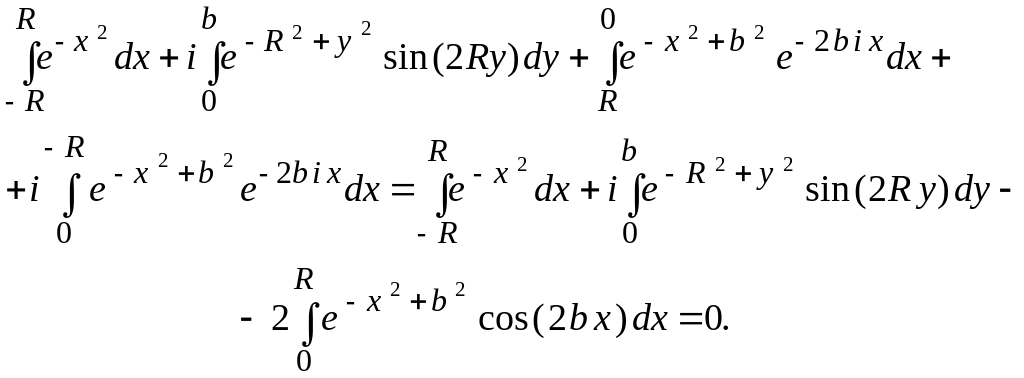
При
R
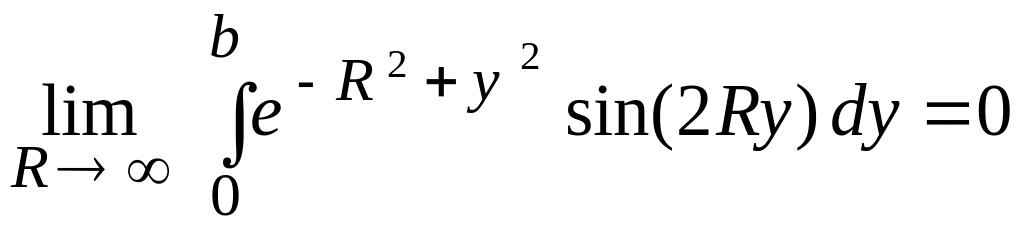 .
.
Таким образом,
![]()
Зная,
что
![]() (интеграл Эйлера – Пуассона), окончательно
имеем
(интеграл Эйлера – Пуассона), окончательно
имеем
![]() .
.
4.3. Интегральная формула Коши
Пусть
функция
аналитическая в ограниченной замкнутой
односвязной области
![]() с кусочно-гладкой жордановой границей
L.
Тогда для любой точки
с кусочно-гладкой жордановой границей
L.
Тогда для любой точки
![]() справедлива формула
справедлива формула
![]() .
(17)
.
(17)
Формула (17) называется интегральной формулой Коши. Для производной n-го порядка справедливо обобщение (17):
![]() .
(18)
.
(18)
Примеры
31.
Вычислить
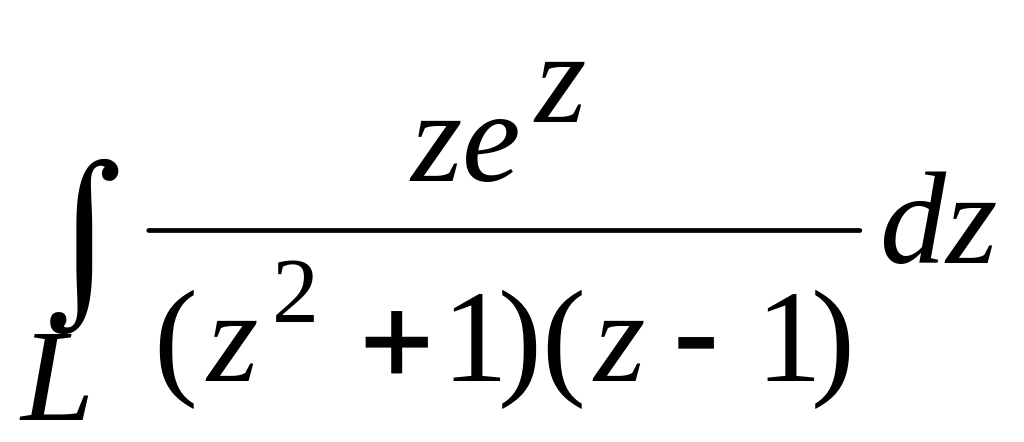 ,
где
,
где
а)
L={z,![]() =1};
b)
L={z,
=1};
b)
L={z,![]() };
c)
L={z,
};
c)
L={z,![]() }.
}.
Решение: а) перепишем интеграл в виде
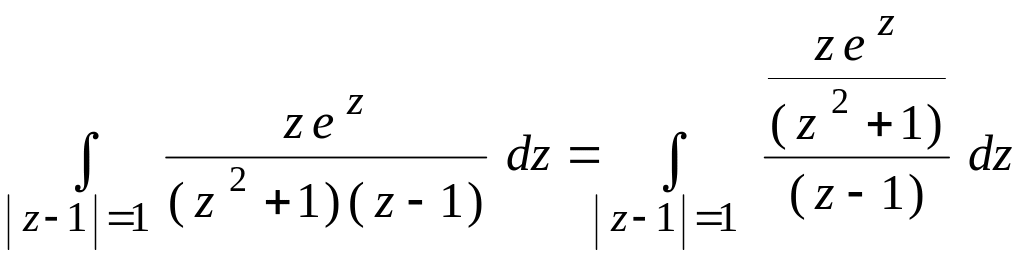 ,
,
функция
![]() – аналитическая в области
– аналитическая в области
![]() ,
а точка
,
а точка
![]() ,
тогда из (25) имеем
,
тогда из (25) имеем
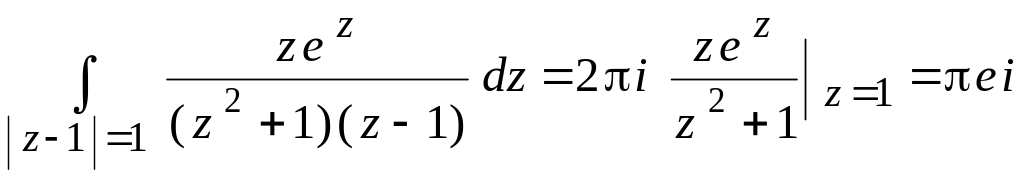 ;
;
b)
в области | z | = ![]() подынтегральная функция
подынтегральная функция
![]() – аналитическая, поэтому из интегральной
теоремы Коши (16) имеем
– аналитическая, поэтому из интегральной
теоремы Коши (16) имеем
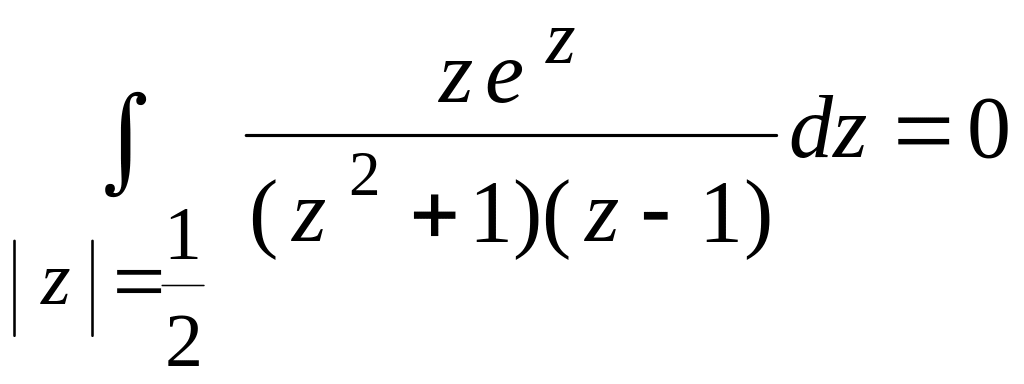 ;
;
с)
в области | z
– 1 – i
| <
![]() лежат две точки, в которых знаменатель
обращается в ноль:
лежат две точки, в которых знаменатель
обращается в ноль:
![]() ,
поэтому воспользоваться непосредственно
формулой (17) невозможно. Разложим функцию
на сумму простых дробей
,
поэтому воспользоваться непосредственно
формулой (17) невозможно. Разложим функцию
на сумму простых дробей
![]() .
.
Тогда, применяя (25) к каждому из интегралов, имеем
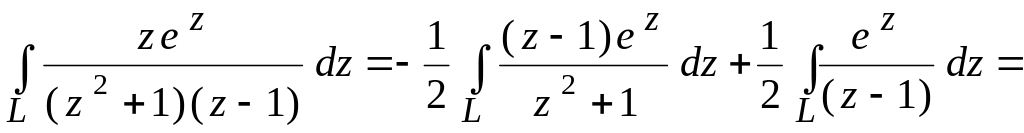
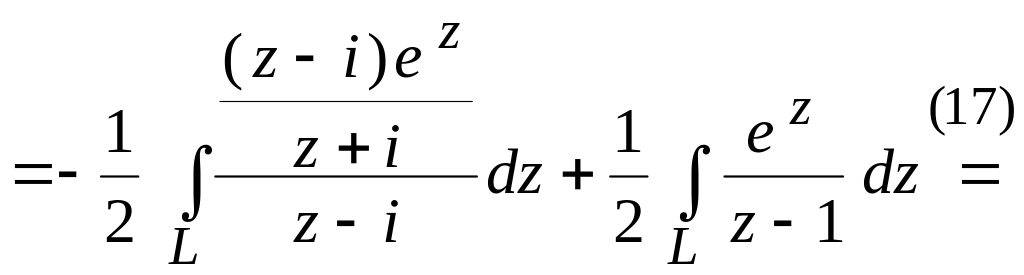
![]() .
.
32.
Доказать, что
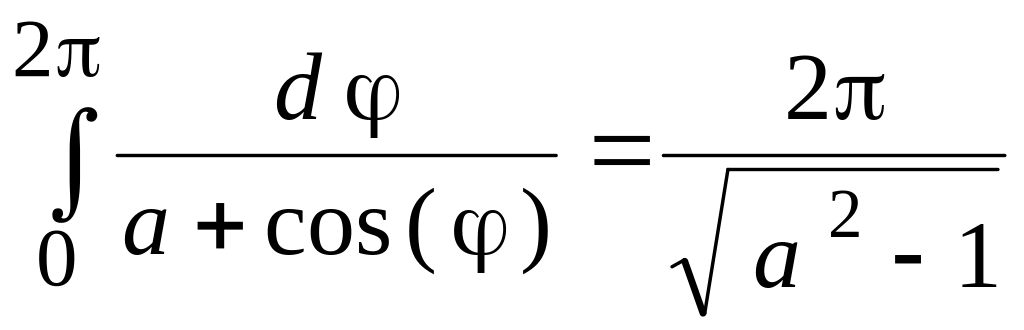 (
(![]() ).
).
Решение.
Заменой
![]() сведем интеграл
сведем интеграл
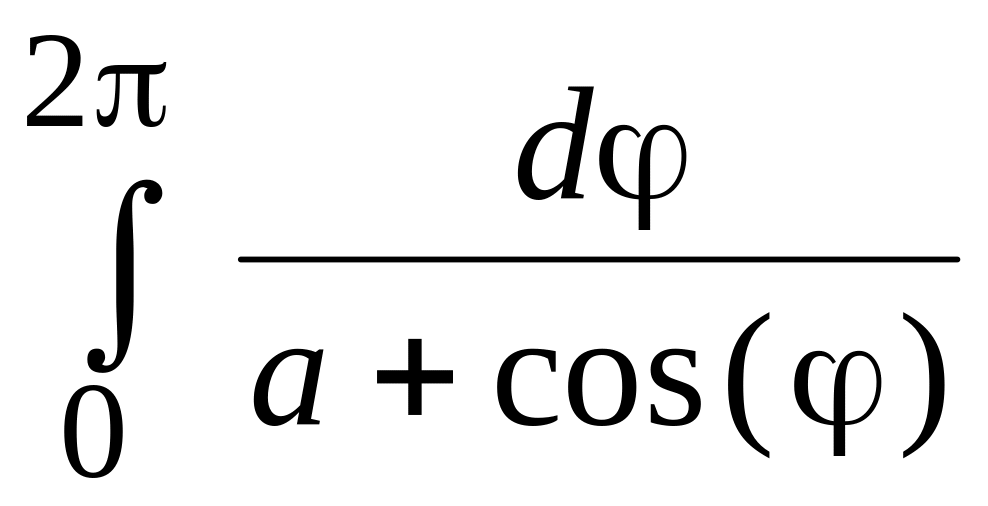 к интегралу по контуру от функции
комплексной переменной. Так как
к интегралу по контуру от функции
комплексной переменной. Так как
![]() ,
воспользовавшись формулой
,
воспользовавшись формулой
![]() ,
имеем
,
имеем
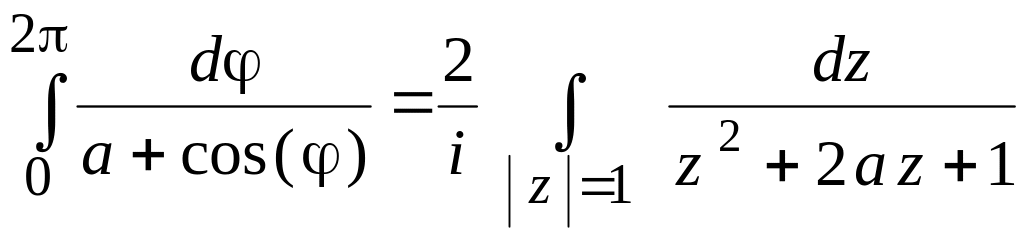 .
.
Разложим знаменатель на множители:
![]() .
.
Точка
![]() точка
точка
![]() ,
таким
образом, функция
,
таким
образом, функция
![]() –
аналитическая в
–
аналитическая в
![]() и
из формулы (17) имеем
и
из формулы (17) имеем
![]()
 .
.
33.
Вычислить
![]() .
.
Решение. Воспользовавшись (17), имеем
![]()
![]() .
.
34.
Вычислить
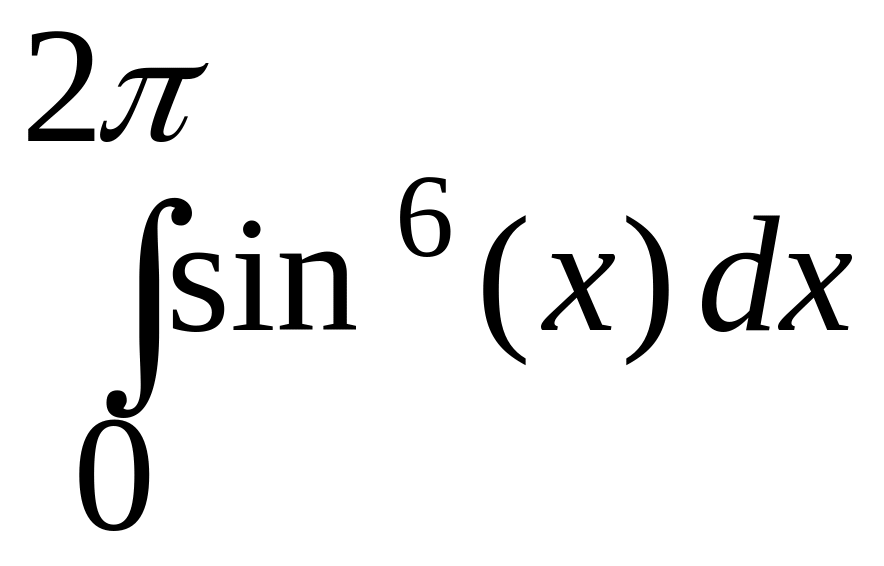 .
.
Решение.
Сделав замену
![]() и используя формулу
и используя формулу
![]() ,
,
имеем
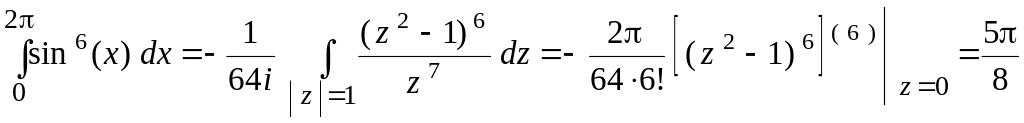 .
.
