Примеры

41. Определить характер изолированной особой точки для функции :

1) 2) .

Решение: 1)

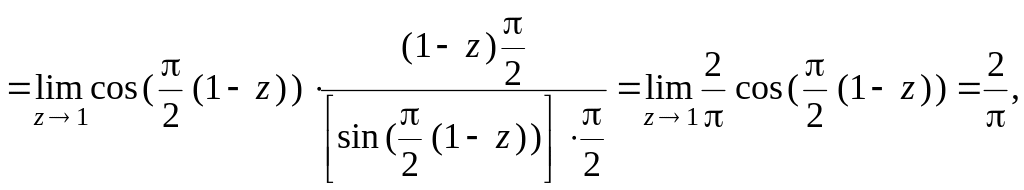
­ – устранимая особая точка ;

Решение: 2)

–­ устранимая особая точка .

42. Найти полюсы функции и определить их кратности:

1) ; 2) .

Решение: 1) запишем функцию в виде

Имеем

.

Точки и – нули знаменателя, причем – нуль третьего порядка, а – простой нуль. Числитель в этих точках в нуль не обращается, поэтому точки и будут соответственно полюсами 3-го и 1-го порядка функции .

Решение: 2) нулями знаменателя будут точки . Разложим знаменатель в ряд:

.

Точка – нуль пятого порядка функции , поэтому – полюс пятого порядка . Точки , – простые нули знаменателя, поэтому они будут простыми полюсами .

43. Определить характер точки для функции .

Решение. Докажем, что не существует. Выберем две последовательности:

.

Для них

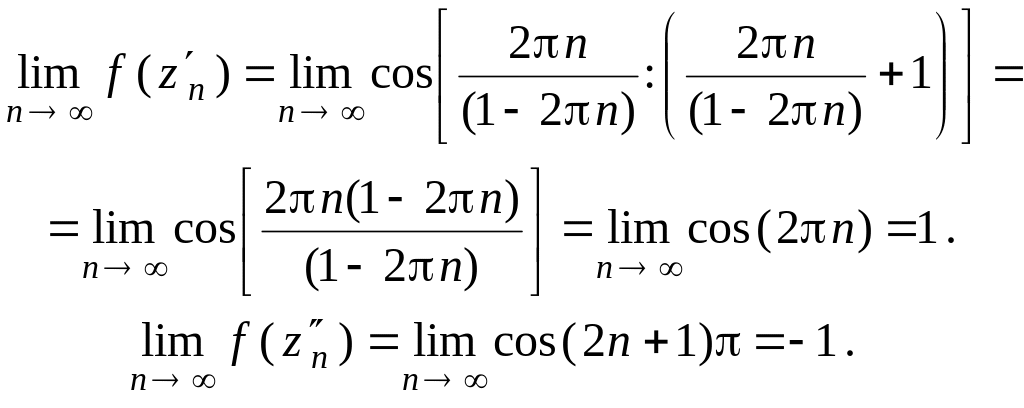
Таким образом, .

Значит, – существенно особая точка .

Глава 6. Вычеты

6.1. Вычисление вычетов

Пусть – изолированная особая точка однозначной аналитической в проколотой окрестности точки функции , L – замкнутый жорданов кусочно-гладкий контур, содержащий внутри себя точку и лежащий целиком в окрестности .

Определение 18. Вычетом функции в точке называется интеграл:

. (31)

Вычет функции в точке равен коэффициенту при первой отрицательной степени в разложении функции в ряд Лорана в окрестности , т.е.

.

Если , то

,

где – замкнутый жорданов кусочно-гладкий контур, содержащий внутри себя начало координат и полностью лежащий в окрестности бесконечно удаленной точки, где аналитична, причем означает, что обход осуществляется в отрицательном направлении. Кроме того

.

В зависимости от типа изолированных особых точек приведем формулы для вычисления вычетов .

1. Пусть – устранимая особая точка функции . Тогда

, если ;

, если . (32)

2. Пусть – полюс n-го порядка, , тогда

, (33)

в частности при n = 1

.

Если – простой полюс и , где и – аналитические функции в точке , причем , то

, (34)

если , где аналитична в точке , то

3. Если – существенно особая точка , то, раскладывая в ряд Лорана по степеням , находим , тогда

.

Заметим еще, что, если – четная функция, то

и ,

если – нечетная, то

. (35)

ОСНОВНАЯ ТЕОРЕМА О ВЫЧЕТАХ. Если – изолированные конечные особые точки функции , аналитической, кроме этих точек во всей комплексной плоскости, то

. (36)

Примеры

44. Вычислить вычет функции в точке :

1) .

Решение. Точка – простой полюс , так как

.

Поэтому из формулы (48)

.

2) .

Решение. Точка – полюс 1-го порядка, так как знаменатель функции имеет в точке нуль первого порядка, так как:

и .

Представим

, где

причем , из (34) имеем

.

3) .

Решение. Точка – полюс 2-го порядка, так как знаменатель в точке имеет нуль 2-го порядка. Из формулы (33) имеем

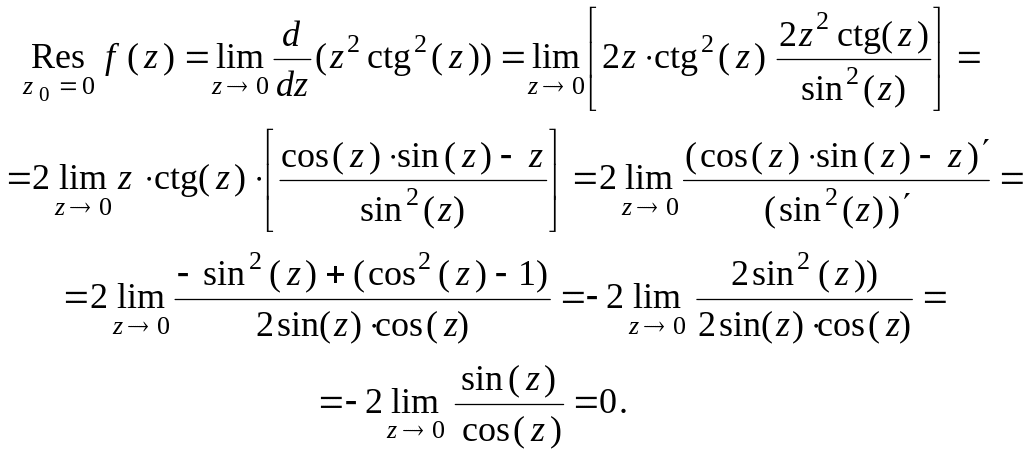
4) Подсчитать вычеты во всех особых точках.

Решение. Точки Z, – простые полюсы, из формулы (32) имеем

Z, .

Точка – полюс второго порядка, так как знаменатель в имеет нуль второго порядка. Разложим в ряд Лорана в окрестности :

Выполняя деление рядов

–

,

–

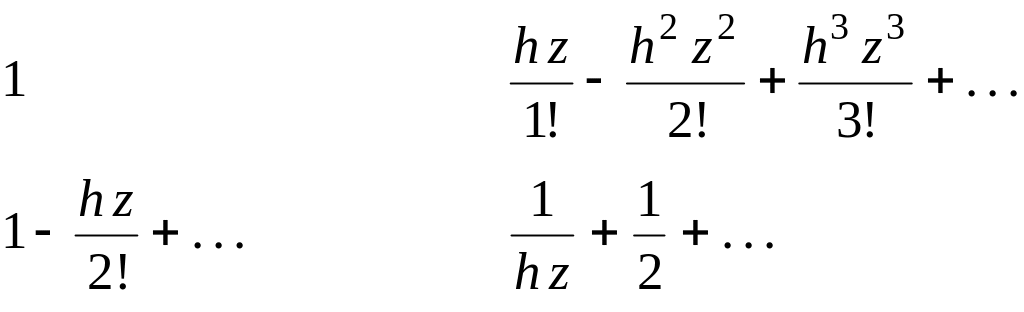
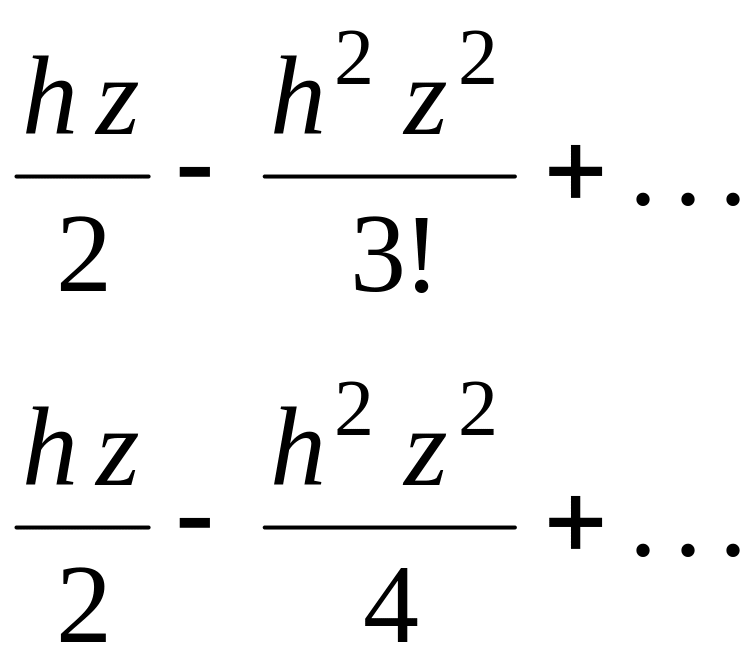
получаем

.

Отсюда: и .

5)

Решение. Так как

,

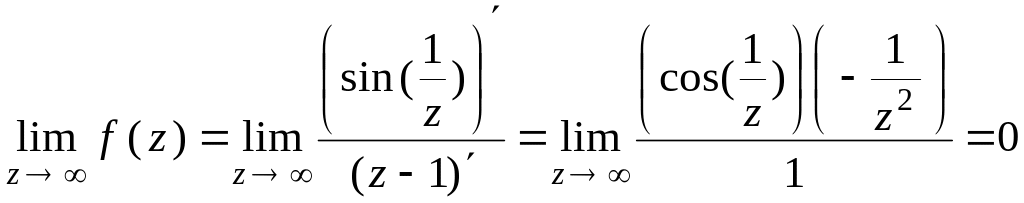то – устранимая особая точка. Воспользовавшись формулой (32), найдем

6)

Решение. Точка – существенно особая точка. Разложим функцию в ряд, воспользовавшись формулами (22) и (26):

,

Перемножая два ряда, найдем коэффициенты при первой отрицательной степени :

.