Примеры

21. Найти:

а) найти модуль функции и выделить ее действительную и мнимую части;

b) значение выражения:

.

22. Доказать:

а) выражение принимает только одно значение, если b – целое, и конечное число значений, если b – рациональное;

d) при фиксированном z разные значения степенной функции :

1) лежат на окружностях, радиусы которых образуют бесконечную геометрическую прогрессию, а аргументы их значений – бесконечную арифметическую прогрессию, если ;

2) лежат на окружностях радиуса , а аргументы этих значений образуют бесконечную арифметическую прогрессию, если .

3.4. Функция Жуковского

Определение 8. Функция

(7)

называется функцией Жуковского.

Эта функция аналитична в точках , причем однолистна, в частности, в следующих областях:

а) – внешность единичного круга,

b) – единичный круг,

с) – верхняя полуплоскость,

d) – нижняя полуплоскость.

Положив в (7) , получим

. (8)

Отсюда следует, что образом окружности – фиксировано) является эллипс

(9)

с полуосями и с фокусами в точках .

Исключая из уравнений (9) параметр при , получим уравнение эллипса в каноническом виде

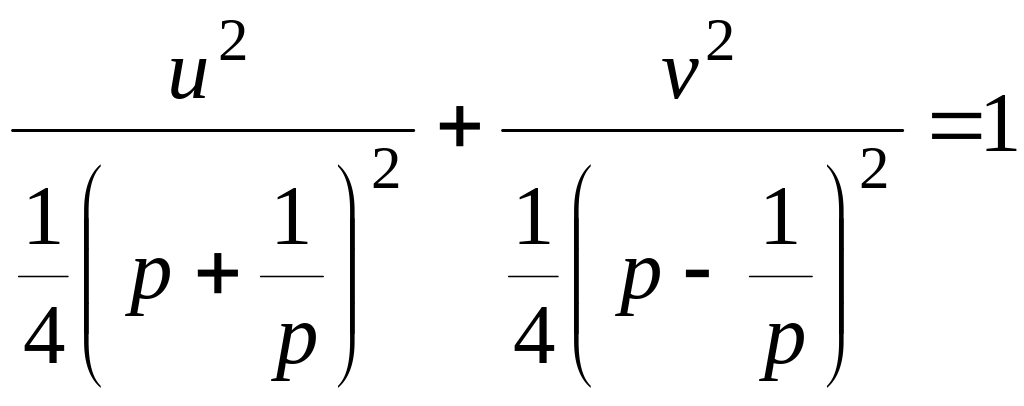. (10)

При замене р на эллипс (10) остается тем же самым, но его ориентация меняется на противоположную.

Таким образом, окружности , ориентированные по часовой стрелке, переходят в эллипсы (10), ориентированные также по часовой стрелке. При отображении окружностей , ориентация меняется на противоположную.

При эллипс (9) вырождается в отрезок , проходимый дважды, т.е. окружность переходит в отрезок , проходимый дважды. Таким образом, функция Жуковского конформно отображает внешность (внутренность) единичного круга на внешность отрезка (рис. 4).

Из (8) следует, что образом луча , , ( – фиксировано), является кривая

, , . (11)

Исключая параметр , при ( – целое), получаем

. (12)

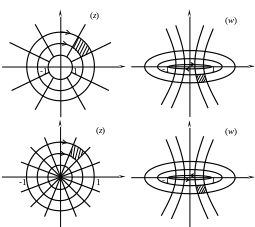
Рис. 4

Кривая (12) – гипербола с фокусами в точках и с асимптотами . Если , то кривая (11) является правой ветвью гиперболы (12), т.е. луч , переходит в правую ветвь гиперболы (ориентация показана на рис. 5), при – в левую ветвь (в (11) заменяем на ). При замене в (11) на получаем ту же ветвь гиперболы, но с противоположной ориентацией. При (луч ) кривая (11) вырождается в луч , проходимый дважды, луч переходит в луч , проходимый дважды, лучи и переходят в мнимую ось . Отсюда следует, что функция Жуковского конформно отображает верхнюю полуплоскость на плоскость с разрезами по лучам и (аналогично нижнюю полуплоскость ).

Рис. 5

Любой эллипс (10) пересекается с любой гиперболой (12) под прямым углом.

Примеры

23. Найти образы заданных областей при отображении :

1) ; 8) ;

2) ; 9) ;

3) ; 10) ;

4) ; 11) ;

5) ; 12) .

6) ;

7) ;

Функция является обратной к функции Жуковского, она аналитична в плоскости с выколотыми точками , а в плоскости с разрезом, соединяющим точки , распадается на две регулярные ветви и , где , . Из свойств функции Жуковского следует, что функция конформно отображает плоскость с разрезом по отрезку на внешность единичного круга, а функция – на круг .