Глава 5. Степенные ряды
5.1. Понятие степенного ряда Определение 9. Степенным рядом называется функциональный ряд вида
,
(18)
где
C,
n
= 0,1,2,... – фиксированные числа.
Определение
10.
Радиусом
сходимости степенного ряда называется
число R,
,
обладающее тем свойством, что при любом
z,
для которого
,
этот ряд сходится, а при любом z,
для которого
,
ряд расходится. Круг
,
где R
– радиус сходимости степенного ряда,
называется его кругом сходимости. Если
ряд сходится только при
,
то по определению полагают
,
если же ряд сходится при всех zC,
то считают что R
=
+.
Для радиуса сходимости степенного ряда
(18) справедлива формула Коши – Адамара
.
(19)
Примеры
35. Найти радиусы сходимости рядов:
1)
; 4)
;
2)
; 5)
3)
; 6)
.
Решение:
1) по формуле (19) имеем
,
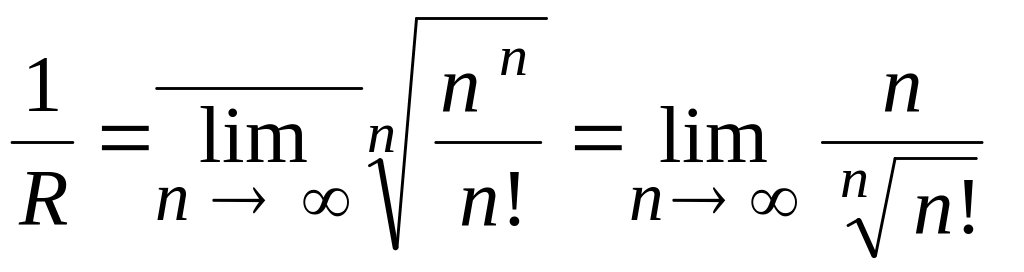для вычисления последнего предела
воспользуемся формулой Стирлинга
,
тогда
,
откуда
;
2)
– степенной ряд, у которого многие
коэффициенты равны нулю. Прежде, чем
воспользоваться формулой Коши – Адамара,
запишем выражения коэффициентов
этого ряда
через номер коэффициента
(здесь
– коэффициент при k-й
степени z):
Так как требуется найти верхний предел неотрицательной последовательности, можно не рассматривать ее нулевые члены. Поэтому
.
5.2. Ряд Тейлора
Пусть
однозначна и аналитична в области D,
точка
и R
– кратчайшее расстояние от точки
до границы области D.
Тогда в круге
функция разлагается в степенной ряд по
степеням
:
, (20)
где
коэффициент
вычисляется по формуле
.
Определение
11.
Степенной ряд (20) называется рядом
Тейлора функции
в окрестности точки
.
Как правило, прямое вычисление коэффициентов рядов Тейлора через вышеприведенные формулы затруднительно и приходится прибегать к различным искусственным приемам. При этом важную роль играет теорема единственности разложения функций в степенной ряд: если функция f представима в круге как сумма степенного ряда, то коэффициенты этого ряда определяются однозначно.
Приведем
разложение некоторых элементарных
функций в точке
:
,
(21)
,
(22)
,
(23)
,
(24)
,
(25)
(26)
(здесь ln (z) – главная ветвь логарифма),
,
(27)
(здесь
– главная ветвь степенной функции).
В частности из формулы (27) имеем
.
(28)
Приведем примеры разложения функций в ряды с использованием формул (21) – (28).
Примеры
36. Разложить в степенной ряд функции:
1)
.
Решение. Из формулы (28) для имеем
.
2)
.
Решение. Из теоремы о почленном дифференцировании степенных рядов имеем
.
3)
.
Решение. Записав данную функцию в виде
и воспользовавшись формулой
(28), для всех
имеем
4)
.
Решение. Воспользовавшись методом неопределенных коэффициентов, разложим функцию на простейшие дроби:
;
Получаем
.
Применяя к каждой из дробей формулу (28), получим
,
,
и
,
.
Отсюда
для всех
5)
.
Решение.
Для всех точек z
окрестности точки
радиуса
:
;
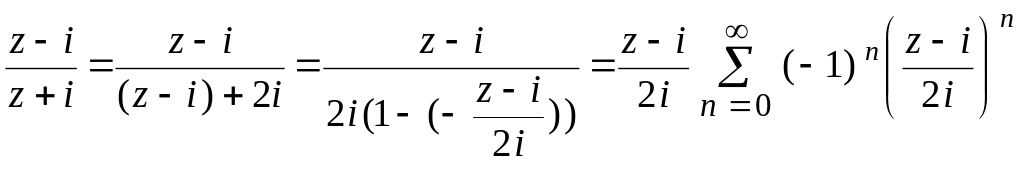так как
,
то имеем
.
6)
.
Решение. Пользуясь тригонометрическими формулами, получаем
.
Из разложений (22), (23):
Окончательно имеем
,
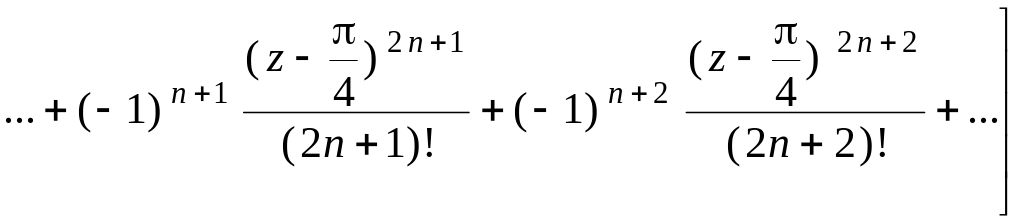C.
7)
Решение. Из разложения (21) имеем
.
8)
Решение. Пользуясь тождеством
и формулой (28), получаем
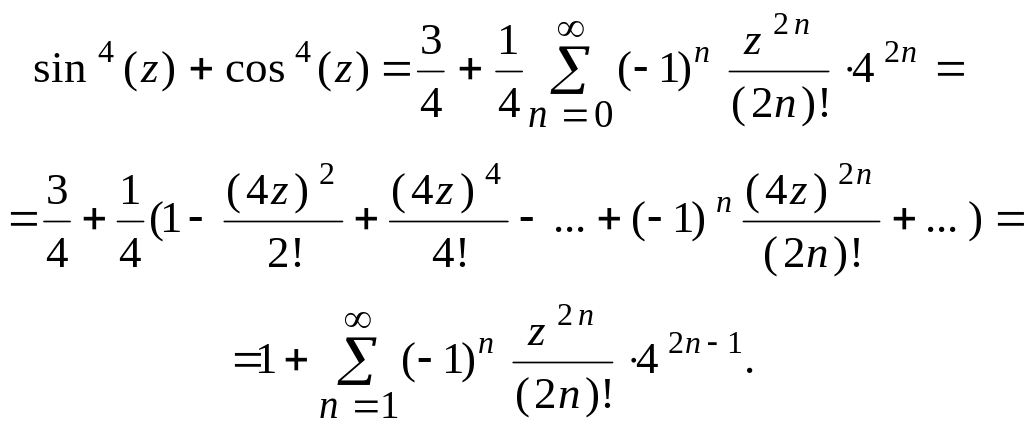
9)
.
Решение. Для разложения функции в степенной ряд преобразуем ее, воспользовавшись формулами Эйлера:
.
Тогда
.
Замечая, что
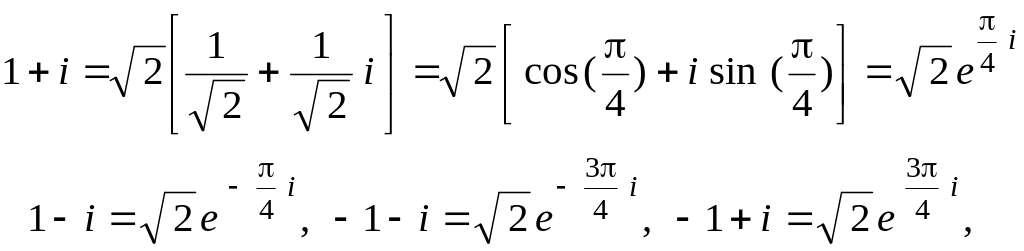
получаем
.
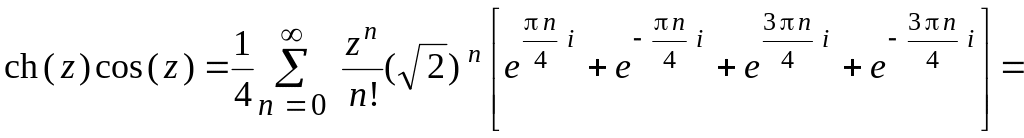
Кроме того:
т.е.
Отсюда окончательно имеем
10)
.
Решение. Используя формулу (21), получаем
.
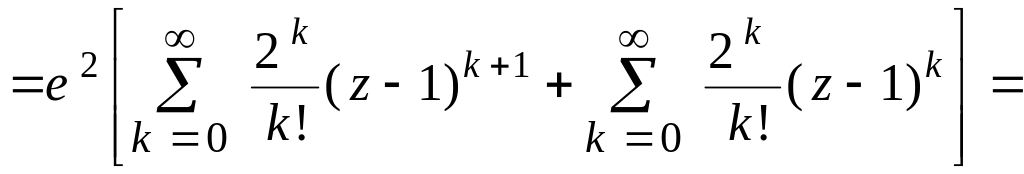
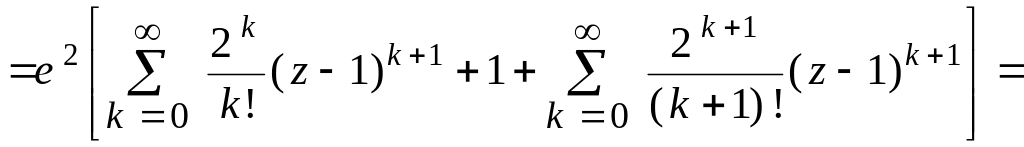
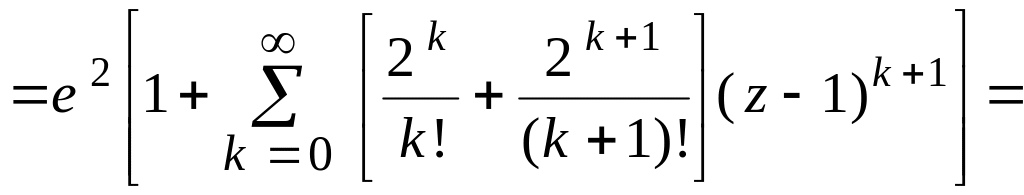
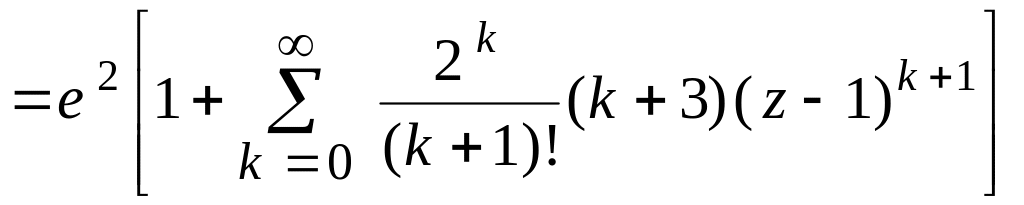При
разложении в ряд некоторых функций, а
именно функций, после дифференцирования
которых получается рациональная дробь,
целесообразно использовать теоремы о
почленном дифференцировании и
интегрировании равномерно сходящихся
рядов (функций вида
,
,
).
Пример
37.
Разложить в ряд Тейлора в окрестности
точки
функцию
.
Решение. Продифференцируем функцию
.
Из формулы (27) имеем
,
Тогда
.
Проинтегрировав почленно последнее равенство, получим
,
где
.