Примеры

3. Найти образ окружности, заданной уравнением

,

при отображении .

Решение. На основании кругового свойства дробно-линейного отображения окружность переходит в окружность. Для ее нахождения на заданной окружности выберем три точки, например: , , образами которых при отображении будут точки . Точками однозначно определяется образ данной окружности, уравнение которой:

. (3)

Для отображения имеем

.

Выразив отсюда и подставив в уравнение заданной окружности, получим искомый образ (3).

4. Найти образ области D при отображении , где .

Решение. Выделим действительную и мнимую части функции w. Имеем:

.

Будем искать образ границы области D (рис. 2).

С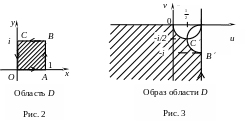 торона отображается на отрицательную часть действительной оси ( ) (рис. 3).

Сторона , отображается в линию .

Сторона , отображается в линию, параметрическое уравнение которой имеет вид

.

Исключив параметр , получим

.

Аналогично образ стороны определяется уравнением

.

В соответствии с принципом соответствия границ образом квадрата будет заштрихованная область на рис. 2.

5. Найти дробно-линейное отображение, которое точки и оставляет неподвижными, а точку переводит в точку . Найти образ полуплоскости при данном отображении.

Решение. По условию имеем три пары соответствующих точек

Применяя формулу (2), получим искомое дробно-линейное отображение

Найдем теперь образ верхней полуплоскости, границей которой является действительная ось. Согласно круговому свойству действительная ось отображается в окружность. Чтобы найти ее, на действительной оси выберем три точки, например: , образами которых будут точки . Они лежат на окружности . По принципу соответствия границ получаем, что образом верхней полуплоскости будет область .

6. Найти дробно-линейное отображение, которое круг отображает на полуплоскость так, что .

Решение. Условие задачи определяет две пары соответствующих точек. Третью пару найдем, пользуясь свойством симметрии дробно линейного отображения, согласно которому точки и , симметричные относительно окружности , перейдут в точки и , симметричные относительно прямой . Таким образом, найдена третья пара точек и .

По формуле (2) найдем искомое отображение .

3.2. Показательная и тригонометрические функции комплексного аргумента

Определение 2. Функция называется показательной и обозначается или .

Примеры

7. Доказать, что любая полоса шириной 2, стороны которой параллельны действительной оси, является областью однолистности функции .

Доказательство. Пусть и – две различные точки комплексной плоскости. Очевидно, что при условии имеем . Отсюда, так как при Z, имеем

.

Таким образом, условие однолистности нарушается для точек и , для которых , где k – любое целое число. Такому условию не удовлетворяет множество точек z комплексной плоскости, для которых , где h – любое действительное число. Отсюда следует, что полоса шириной , стороны которой параллельны действительной оси, является областью однолистности.

8. Доказать, что при отображении :

а) образом прямой является луч, выходящий из начала координат под углом к положительному направлению действительной оси;

b) образом прямой является окружность с центром в начале координат и радиусом .

Доказательство: а) действительно, так как , то , , тогда , что означает, что изменяется от 0 до , т.е. образом прямой является луч ;

b) так как , то , , тогда , т.е. , , а это – параметрическое уравнение окружности с центром в начале координат и радиусом .

Тригонометрические и гиперболические функции комплексной переменной задаются формулами:

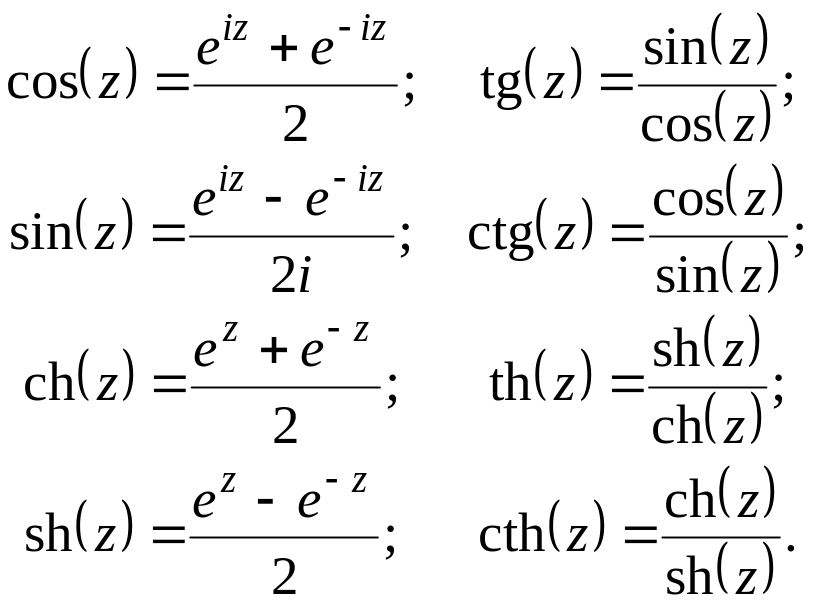
9. Доказать соотношения между тригонометрическими и гиперболическими функциями:

1) ;

2) ;

3) ;

4) .

10. Пусть . Доказать, что

1) ;

2) ;

3) ;

4) .

11. Найти образы прямых при отображении .

Решение. Для отображения имеем , (см. пример 8). При этом отображении прямая ( ) переходит в кривую, параметрическое уравнение которой

.

Исключая параметр , получаем

( ), (4)

причем координата u сохраняет знак, равный , а координата v пробегает всю числовую ось. Тогда образом прямой ( ) является одна ветвь гиперболы (4) с полуосями |sin(a)| и |cos(a)| и с фокусами в точках ±1. Если , то прямая превращается в кривую, параметрическое уравнение которой , т.е. в мнимую ось плоскости w. Если , то прямая переходит в кривую, параметрическое уравнение которой , т. е. в луч при нечетном k и в луч при четном k.

Аналогично образом прямой , является эллипс

с полуосями и и с фокусами в точках ±1. Если , то образом действительной оси в плоскости является отрезок действительной оси плоскости .

12. Доказать, что: 1) функция полосу отображает на всю плоскость с разрезами по лучам и действительной оси ; 2) функция полосу отображает на всю плоскость с разрезами по лучам и действительной оси .