Примеры
24. Найти образы области :
1)
при отображениях ветвями
и
,
где
,
и
– плоскость
с разрезами по лучам
и
;
2)
,
,
;
3)
,
,
;
4)
,
,
;
5)
,
,
при
;
6)
,
,
,
;
7)
,
,
.
3.5. Конформные отображения, определяемые комбинациями основных элементарных функций
Основные задачи теории конформных отображений имеют следующий вид: даны области и , требуется найти функцию , осуществляющую конформное отображение области на область .
Один из методов поиска функции , если такую функцию можно найти, основан на подборе надлежащим образом элементарных функций, рассмотренных ранее.
Примеры
25. Найти конформное отображение области D на область G, если:
1)
,
;
2)
,
;
3)
,
;
4)
,
;
5)
,
;
6)
,
;
7)
,
;
8)
,
;
9)
,
;
10)
,
;
11)
,
.
Решение:
1) область
ограничена полуокружностью
,
и лучами
и
,
которые пересекаются с полуокружностью
в точках
под прямым углом (рис 6, а).
Дробно-линейная функция
(13)
точку
переводит в точку
,
а точку
– в точку
.
Пользуясь
свойством сохранения углов при конформном
отображении, получим, что область
отображением (13) переводится на
внутренность прямого угла с вершиной
в точке
.
Одна из сторон этого угла – положительная
часть мнимой оси (образ полуокружности),
другая – положительная часть действительной
оси (образы лучей
и
)
(рис 6, б).
Функция
переводит квадрант на верхнюю
полуплоскость, т.е. функция
осуществляет
отображение области
на верхнюю полуплоскость (рис. 6, в);
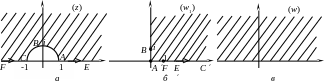
Рис. 6
2)
с помощью степенной функции
данный сектор (рис. 7, а)
переводится на верхний полукруг радиуса
(рис. 7, б).
Легко видеть, что дробно-линейная функция
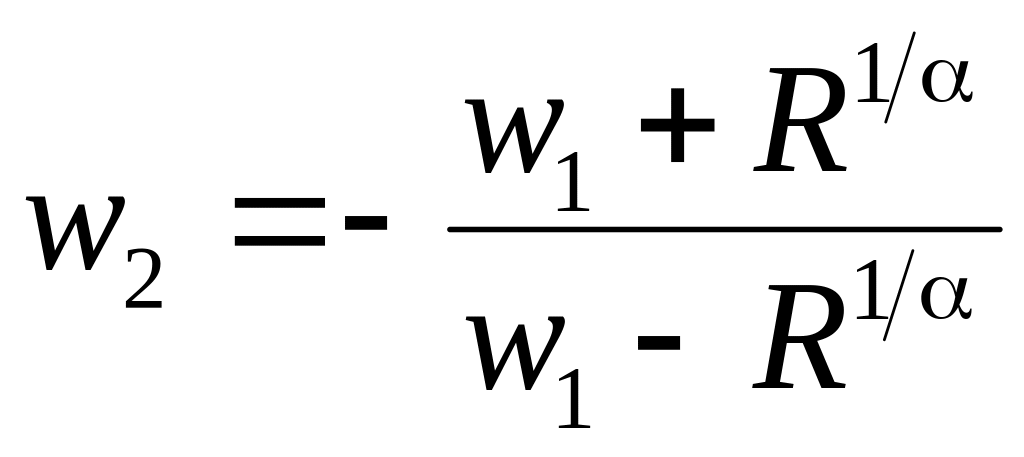внутренность полукруга
,
(рис. 7, б),
отображает на первый квадрант плоскости
(рис. 7, в).
Отображением
этот квадрант переводится на верхнюю
полуплоскость (рис. 7, г).
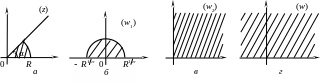
Рис. 7
Итак,
искомое отображение имеет вид
;
4)
область
является внутренностью угла с разрезом
по лучу
(рис. 8, а).
Отображение
переводит область
на всю комплексную плоскость с разрезом
по лучам
и
(рис. 8, б),
а отображение
,
переводит эту область на верхнюю
полуплоскость (рис 8, в).
Тогда отображение
переводит
верхнюю полуплоскость плоскости
на полосу
(рис 8, г).
То есть функция
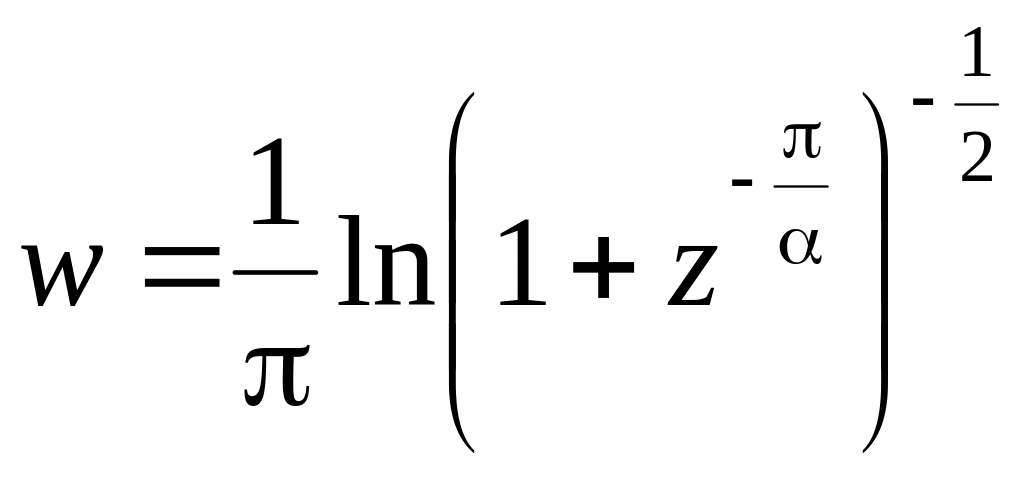осуществляет
искомое отображение
(рис. 8, а
и г).
Р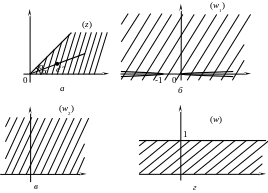
ис.
8
Глава 4. Интеграл от функции комплексной переменной
4.1. Понятие интеграла от функции комплексной переменной
Пусть
– непрерывная функция в области
комплексной плоскости;
– кусочно-гладкая кривая, лежащая в
области
с началом в точке
и концом в точке
.
Разобьем
кривую
произвольным образом на
элементарных частей
точками
.
Составим сумму
,
где
,
,
.
Пусть
,
– длина дуги кривой
,
a
.
Тогда
называется интегралом от функции по кривой .
Если
кривая
задается уравнением
,
,
то вычисление интеграла от функции
по кривой
(в порядке возрастания парамет-
ра
)
сводится к вычислению определенного
интеграла по формуле
.
(14)
Если
,
то интеграл (19) сводится к вычислению
криволинейных интегралов
.
(15)