Примеры
47. Вычислить интегралы:
1)
;
2)
;
3)
.
Решение:
1) рациональная функция
аналитична в верхней полуплоскости, за
исключением точки
(полюс второго порядка) и
.
.
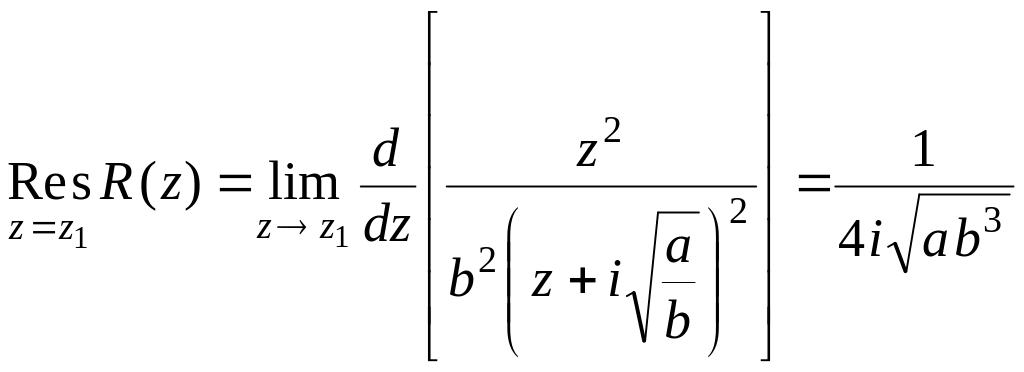Из
(40)
.
Решение:
2) функция
– аналитическая в верхней полуплоскости,
включая действительную ось, кроме точки
(полюс);
,
поэтому из формулы (41):
.
Решение: 3) преобразуем J:
.
Первый интеграл – табличный
.
При
вычислении второго интеграла воспользуемся
формулой (42), учитывая, что
– четная функция:
.
Окончательно:
.
Контрольные работы Контрольная работа 1
Задание к каждому варианту
1. Представить комплексное число z в алгебраической форме.
2. Изобразить на комплексной плоскости множество точек, удовлетворяющих данному условию.
3. Записать комплексное число z в тригонометрической и показательной формах.
4. Используя формулу Муавра, вычислить.
5. Найти корни уравнения и отметить их на комплексной плоскости.
Вариант 1
1.
2.
3.
4.
5.
|
Вариант 2
1.
2.
3.
4.
5.
|
Вариант 3
1.
2.
3.
4.
5.
|
Вариант 4
1.
2.
3.
4.
5.
|
Вариант 5
1.
2.
3.
4.
5.
|
Вариант 6
1.
2.
3.
4.
5.
|
Вариант 7
1.
2.
3.
4.
5.
|
Вариант 8
1.
2.
3.
4.
5.
|
Вариант 9
1.
2.
3.
4.
5.
|
Вариант 10
1.
2.
3.
4.
5.
|
Вариант 11
1.
2.
3.
4.
5.
|
Вариант 12
1.
2.
3.
4.
5.
|
Вариант 13
1.
2.
3.
4.
5.
|
Вариант 14
1.
2.
3.
4.
5.
|
Вариант 15
1.
2.
3.
4.
5.
|
Вариант 16
1.
2.
3.
4.
5.
|
Вариант 17
1.
2.
3.
4.
5. |
Вариант 18
1.
2.
3.
4.
5.
|
Вариант 19
1.
2.
3.
4.
5.
|
Вариант 20
1.
2.
3.
4.
5.
|
Вариант 21
1.
2.
3.
4.
5.
|
Вариант 22
1.
2.
3.
4.
5.
|
Вариант 23
1.
2.
3.
4.
5.
|
Вариант 24
1.
2.
3.
4.
5.
|
Вариант 25
1.
2.
3.
4.
5.
|
|
