5.3. Ряд Лорана
Если
функция
однозначна и аналитична в кольце
,
то она разлагается в нем в ряд
Лорана
,
где
.
При
r
= 0 и R
<
кольцо вырождается в круг с выколотым
центром. Ряды
называются соответственно правильной
и главной частями ряда Лорана.
Определение
12.
Внешность круга
называется окрестностью бесконечно
удаленной точки.
Если
однозначна и аналитична в окрестности
бесконечно удаленной точки (за исключением
может быть только точки z
= ),
то она разлагается в ее окрестности в
ряд
,
называемый рядом Лорана функции f в окрестности точки z = .
Определение 13. Ряды
называются соответственно правильной и главной частями ряда Лорана в окрестности бесконечно удаленной точки.
Часто нецелесообразно использовать непосредственную формулу для подсчета коэффициентов ряда Лорана, поэтому, как и в случае ряда Тейлора, прибегают к некоторым искусственным приемам.
Примеры
38. Разложить
функцию
в ряд Лорана в окрестности точки
:
1)
;
2)
.
Решение: 1) используя метод неопределенных коэффициентов, разложим рациональную дробь на сумму простых дробей
Получаем
.
Функция
аналитична в круге
,
(особые точки
,
z =
в круг не попадают) и поэтому ее можно
разложить в ряд Тейлора в окрестности
.
Для этого представим
в виде
.
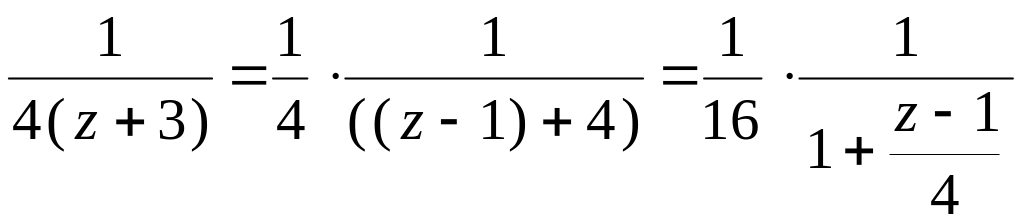Учитывая что
,
имеем
.
Функция
аналитична
в кольце
и уже записана рядом Лорана по степеням
(z – 1). Окончательно
получаем
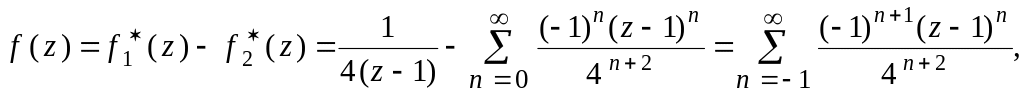где
.
39.
Разложить функцию
в ряд Лорана: a) в кольце
;
b) в окрестности
бесконечно удаленной точки.
Решение:
а) с помощью метода неопределенных
коэффициентов
можно представить в виде
.
Функция
аналитична во внешности круга
,
поэтому
.
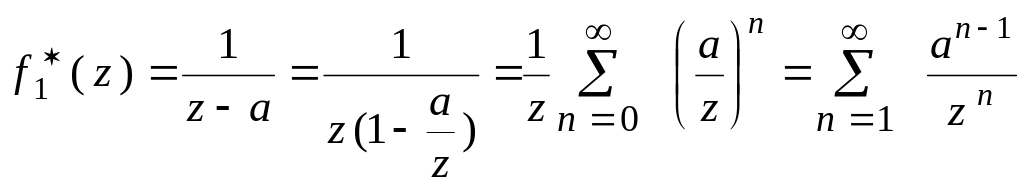Для функции
.
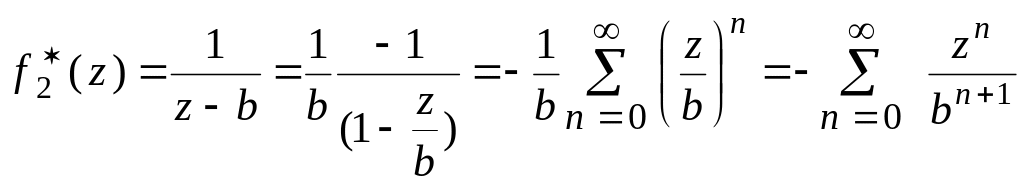Окончательно
.
Решение:
b) окрестностью
бесконечно удаленной точки будет кольцо
,
поэтому из условия
имеем
Получаем
.
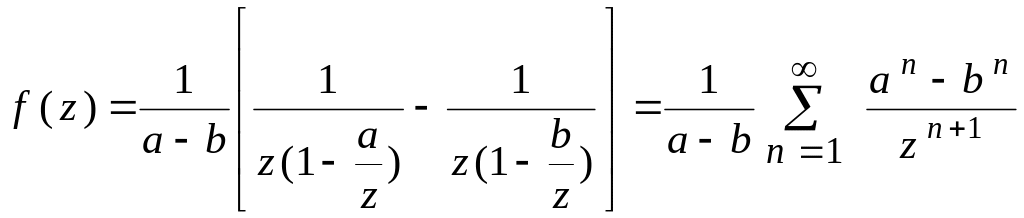40. Разложить
функцию в ряд Лорана в окрестности точки
:
1)
;
2)
Решение: 1)
запишем дробь
в виде
Тогда
Воспользовавшись
стандартными формулами (22) и (23) для
и
,
получаем
где
.
Решение:
2) представим дробь
в виде
и воспользуемся стандартным разложением
(21):
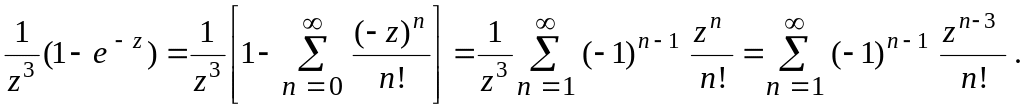
Так
как особые точки функции: z
= 0 и z = ,
то мы получили разложение в кольце
.
Разложить
функцию
в ряд Лорана в области
.
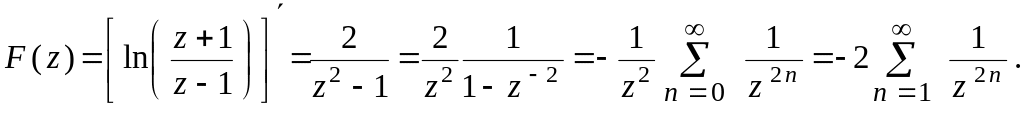
Этот ряд равномерно сходится на любой гладкой кривой, соединяющей точку z c . Интегрируя почленно, находим
.
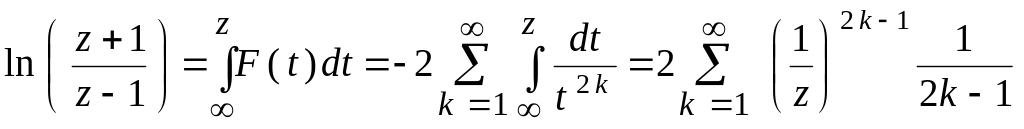5.4. Классификация изолированных особых точек однозначного характера аналитической функции
Определение
14. Точка
называется изолированной особой точкой
однозначного характера функции
,
если в некоторой окрестности этой точки
однозначная функция
аналитична, а в самой точке
не определена или не аналитична.
Бесконечно
удаленная точка называется изолированной
особой точкой однозначного характера
функции
,
если в кольце
однозначная функция
аналитична.
Точки ветвления многозначной функции называются особыми точками многозначного характера. В дальнейшем будем рассматривать только изолированные особые точки однозначного характера.
Классификация изолированных особых точек может быть проведена двумя эквивалентными способами:
по виду лорановского разложения функции в окрестности особой точки ;
по характеру поведения функции в окрестности этой точки.
Определение 15. Точка называется устранимой особой точкой функции если:
1) в разложении в ряд Лорана функции в окрестности отсутствует главная часть ряда, т.е.
,
;
2)
.
Определение 16. Точка называется полюсом порядка n функции , если:
1) в разложении в ряд Лорана в функции окрестности главная часть ряда Лорана содержит конечное число слагаемых, т.е.
,
(29)
(30)
2)
.
Порядок
полюса
функции
равен по определению кратности нуля
функции
в точке
.
Доказывается, что если в окрестности
справедливо представление (29) или (30),
то порядок полюса равен числу n.
Определение 17. Точка называется существенно особой точкой , если:
1) в разложении в ряд Лорана в окрестности главная часть ряда Лорана содержит бесконечно много слагаемых, т.е.
,
;
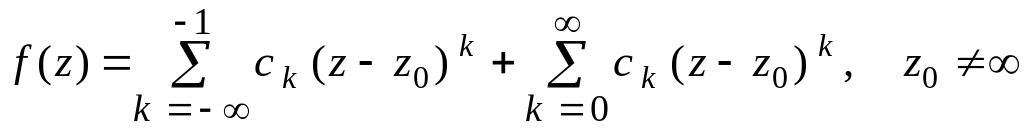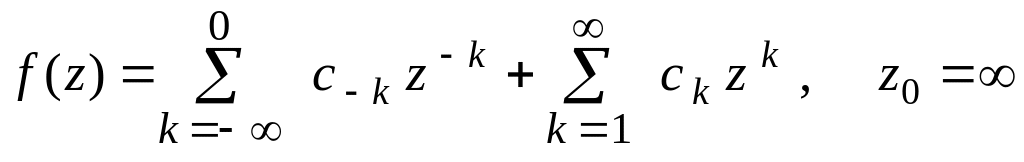2)
не
существует.