
- •Глава 4. Анализ пассивных и активных линейных цепей в области комплексной переменной . (Операторный метод).
- •§1. Преобразование Лапласа, его основные свойства и теоремы.
- •§4. Анализ пассивных (активных) линейных цепей путем преобразования по Лапласу интегрально-дифференциальных уравнений Кирхгофа.
- •§5. Анализ пассивных и активных линейных цепей путем преобразования по Лапласу дифференциальных уравнений состояния.
- •§6. Передаточная функция цепи. Связь передаточной функции цепи с импульсной и переходной характеристиками цепи
- •§7. Вычисление передаточной функции цепи с помощью мун и мкт.
- •§2. Краткое описание аналитически-численного метода решения в обобщенных функциях и функционально-степенных рядах обыкновенных нелинейных интегрально дифференциальных уравнений.
- •§3. Краткое описание процедуры аналитически-численного метода
- •§4. Процедура аналитически-численного метода.
- •Глава 6. Расчет линейных цепей в области комплексной переменной
- •§1. Постановка задачи. Назначение метода. Понятие обобщенного сигнала, комплексной амплитуды и комплексной частоты.
- •§2. Законы Ома для элементов цепи и постулаты Кирхгофа для элементов структуры цепи в s-области.
- •§3. Процедура расчета вынужденных режимов в линейных цепях в области комплексной переменной sс помощью комплексных схем замещения.
- •§4. Процедура расчета линейных цепей в комплексной области с помощью уравнений Кирхгофа или уравнений состояния.
- •§5. Понятие комплексных функций цепи. Связь комплексной функции цепи с дифференциальным уравнением ее динамики.
- •§6. Процедура расчета переходного процесса в линейных цепях в области s.
- •§7. Расчет линейных цепей в установившемся гармоническом режиме.
- •§8. Частотные характеристики rLиRCцепей.
- •§9. Частотные характеристики rlc-цепей. Резонанс в простых колебательных контурах.
- •§1. Постановка задачи. Временное и спектральное представление гармонических и периодических негармонических сигналов, имеющих разложение в ряд Фурье.
- •§2. Законы Ома и Кирхгофа для элементов цепи и элементов структуры цепи в области s. Процедура расчета.
- •§3. Вычисление периодической реакции цепи в замкнутой форме операторным методом.
- •§1. Спектральное представление апериодических сигналов. Преобразование Фурье.
- •§2. Законы Ома и Кирхгофа. Процедура расчета переходного процесса в линейных цепях в частотной области.
- •§3. Использование частотного метода для формирования понятия искаженной передачи сигналов. Прохождение сигналов через цепь с характеристикой идеального фильтра.
- •§4. Примеры прохождения сигналов через дифференцирующие и интегрирующие цепи.
- •Глава 9. Некоторые дополнительные методы расчета цепей.
- •§1. Способ раскрытия определителей без понижения их порядка.
- •§2. Метод сигнальных графов.
- •Глава 10. Основы теории четырехполюсников.
Глава 4. Анализ пассивных и активных линейных цепей в области комплексной переменной . (Операторный метод).
§1. Преобразование Лапласа, его основные свойства и теоремы.
![]()
Предназначено для того, чтобы, преобразовав независимую переменную, упростить решение интегрально-дифференциальных уравнений, позволить получить новые области применения этих методов.
Условия преобразования :![]() .
.
Свойства преобразования Лапласа:
аддитивно:
![]()
однородно:
![]()
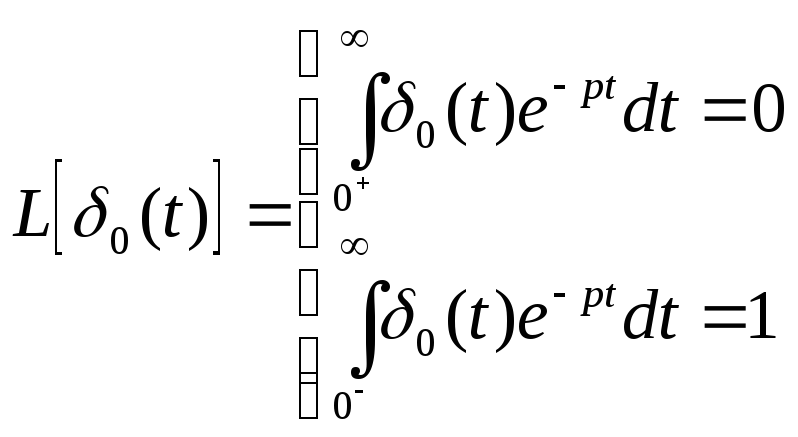
Некоторые основные теоремы преобразования Лапласа.
Дифференцирование в t-области

Дифференцирование в p-области
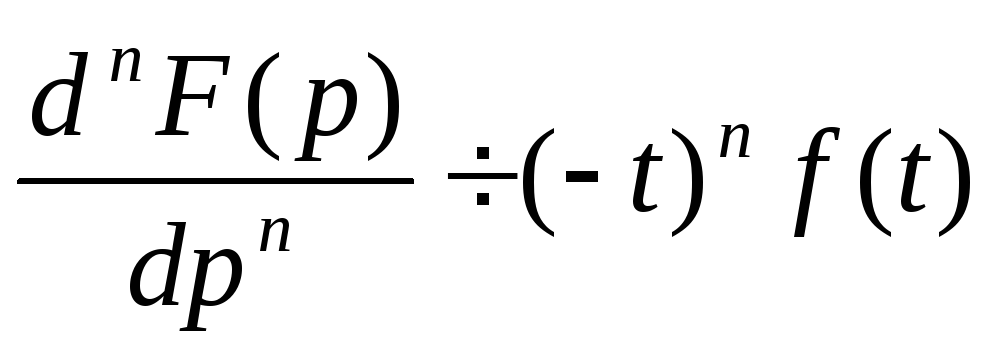
Интегрирование в t-области

Интегрирование в p-области
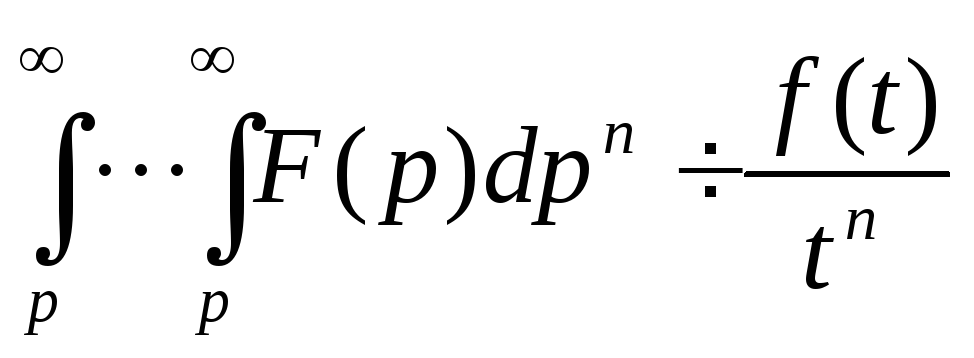
Сдвиг в t-области (запаздывание)

Сдвиг в p-области
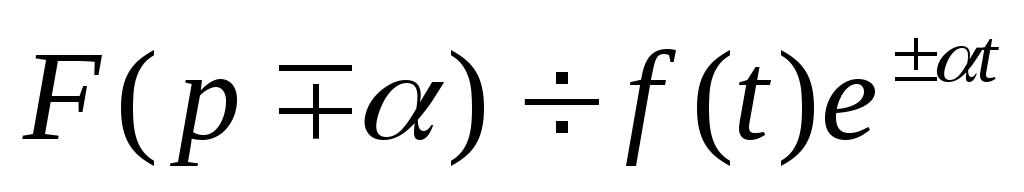
Подобие или правило изменения масштаба независимых переменных
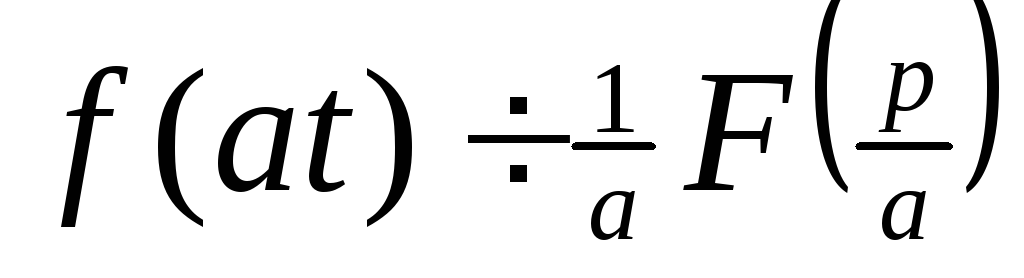
Свертка или правило умножения изображений
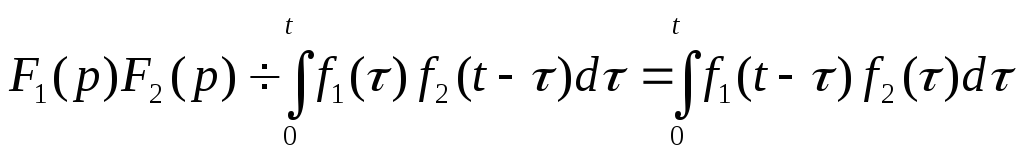
О начальном значении временной функции
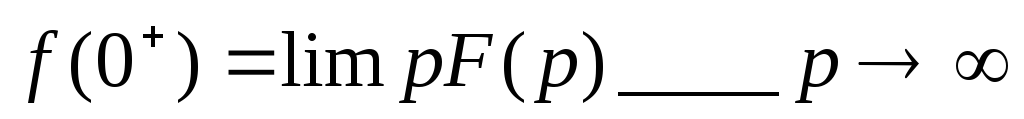
О конечном значении временной функции
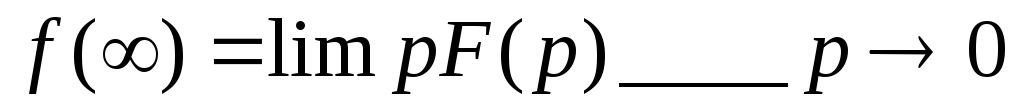
Изображение некоторых временных функций.
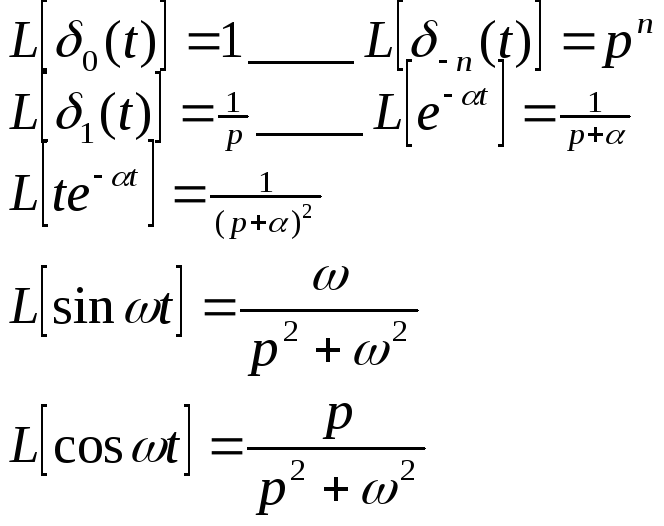
Выводы.
Из теорем 1 и 3 видно, что операции дифференцирования и интегрирования в t-области заменяются соответственно операциями умножения и деления наpвp-области, т.е. интегральные и дифференциальные уравнения, записанные вt-области, имеют алгебраизованные преобразования их по Лапласу, благодаря чему процедура их решения качественно упрощается.
§2. Постановка общей задачи анализа кусочно-линейных цепей в области комплексной переменной p=σ+jω. Вычисление обратного преобразования Лапласа с помощью теоремы Хевисайда.
Постановка общей задачи анализа кусочно-линейных цепей в p-области.

Преобразовать по Лапласу интегральные или дифференциальные уравнения, связывающие ток и напряжение в каждом из элементов цепи, и, следовательно, алгебраизовать уравнение Ома для элементов. Составить из этих элементов алгебраизованную схему электрической цепи и рассчитать ее, описав алгебраическими уравнениями Кирхгофа или с помощью одного из алгебраических методов расчета. В итоге мы получим изображения искомых переменных.
Можно в t-области составить интегрально-дифференциальные или дифференциальные уравнения Кирхгофа, преобразовать его по Лапласу и решить полученное алгебраическое уравнение относительно изображений искомых переменных.
Составить в t-области уравнение состояния, преобразовать его по Лапласу и решить полученное алгебраическое уравнение относительно изображений искомых переменных.
Во всех трех случаях мы получаем изображения искомых переменных, следовательно необходим аппарат для перевода полученного результата в t-область, т.е. преобразование изображениеоригинал.
Вычисление обратного преобразования Лапласа с помощью теоремы Хевисайда.
![]()
Решение алгебраического уравнения в
p-области есть изображение
Х(р), и оно может быть представлено в
видеA(p)X(p)=G(p)F(p),
то .
Если эта дробь неправильная, то для
дальнейшего преобразования надо выделить
целую часть.
.
Если эта дробь неправильная, то для
дальнейшего преобразования надо выделить
целую часть.![]()
![]() изображение складывается из целой части
и правильной дроби.
изображение складывается из целой части
и правильной дроби.
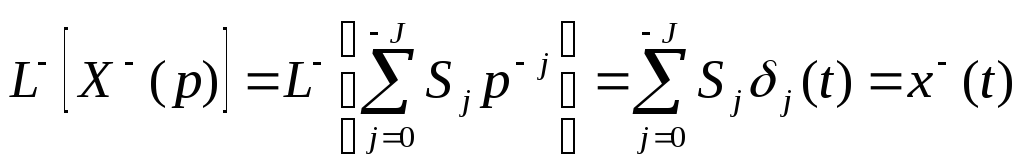 - сингулярная составляющая вt-области.
- сингулярная составляющая вt-области.
Задача заключается в том, чтобы привести в t-областьX+(p).
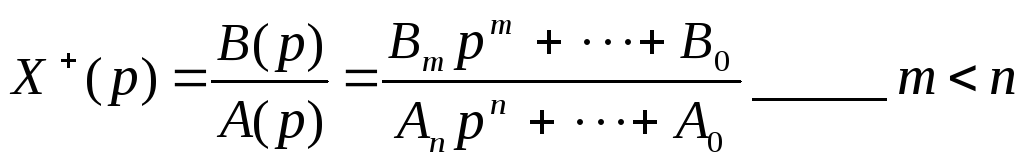
Предложение Хевисайда заключалось в представлении этой функции в виде:
![]() ,
где рi– корни
полинома А(р).
,
где рi– корни
полинома А(р).
Корни полинома piназываются полюсами функции, а коэффициентыai– вычетами.
Предположим, что среди корней полинома нет кратных, тогда:
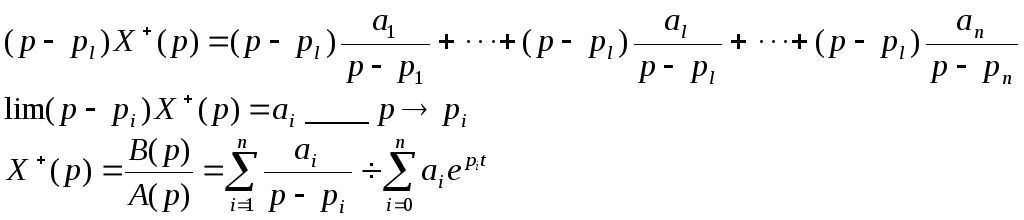
Итог.
Получив в результате решения алгебраическое уравнение в p-области – функцию Х(р), которая в общем случае представляет собой неправильную дробь, мы выделяем из нее целую часть, после чего находим корни полинома знаменателя и записываем результат в виде суммы целой части и суммы элементарных дробей, а затем переводим результат вt-область.
Формула Хевисайда:
![]()
Если среди корней полинома есть кратные, то по формуле Хевисайда вычисляют вычет в форме старшей кратности, а вычеты в корнях младшей кратности вычисляют методом неопределенных коэффициентов.
§3. Уравнение Ома и Кирхгофа для элементов цепи и уравнения Кирхгофа для элементов структуры цепи в операторной форме. Операторные схемы замещения элементов и цепей. Анализ пассивных и активных линейных цепей с помощью их операторных схем замещения.
Уравнения Ома и Кирхгофа в операторной форме для элементов цепи и операторные схемы замещения элементов.
Резистор.
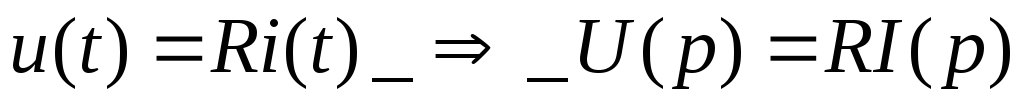
Z(p) – операторное сопротивление. Резистор преобразуется сам в себя.
Индуктивность.
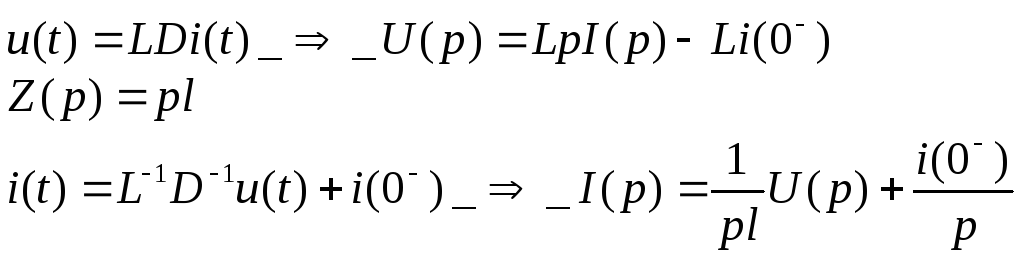

Емкость.
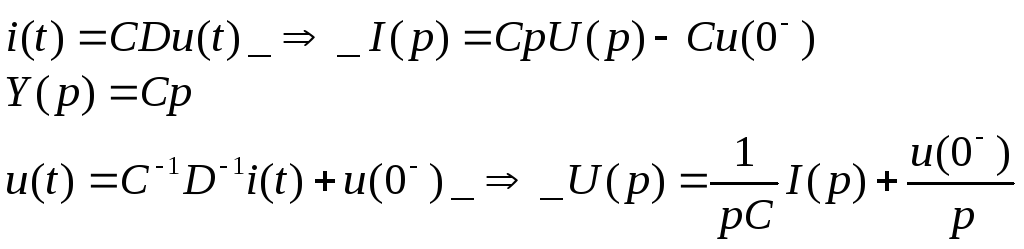
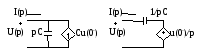
Во всех остальных линейных случаях получим аналогичные результаты.
Уравнения Кирхгофа для элементов структуры цепи.

Q– векторы предначальных условий.
Процедура анализа линейных активных (пассивных) цепей с помощью операторных схем замещения.
Обычным образом в t-области анализируем цепь до коммутации и находим предначальные токи в индуктивностях и напряжения на емкостях.
Преобразуем по Лапласу входные воздействия.
Замещаем все индуктивности и емкости их операторными схемами замещения, выбирая те из них, которые приводят к более простым структурным схемам и строим операторную схему замещения цепи
Построенную операторную схему замещения цепи обычным образом описываем алгебраическими уравнениями Кирхгофа относительно изображений искомых переменных.
Составленную систему уравнений обычным образом решаем, находя изображения искомых переменных.
Найденные изображения с помощью теоремы Хевисайда переводим в оригинал
Проверка подстановкой.
