Контрольные задания

Найти стационарные движения и составить уравнения возмущенного движения для исследования их устойчивости.

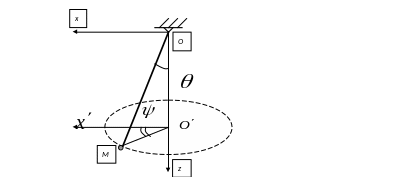
Задача 1. Конический маятник (в переменных Лагранжа) [6]:

Постановка задачи: Рассмотрим материальную точку М массы m , подвешенную на невесомой нити OM в точке О (сферический маятник). Пусть длина нити равна l. Положение точки М будем определять углами , смысл которых очевиден из рисунка.

Ось вертикальна, ось параллельна неподвижной горизонтальной оси Ох , прямая перпендикулярна оси . Для каждого угла существует такая постоянная скорость , что маятник совершает стационарное движение по горизонтальной окружности

Требуется:

1. Составить уравнения движения в форме уравнений Лагранжа 2-го рода

_.

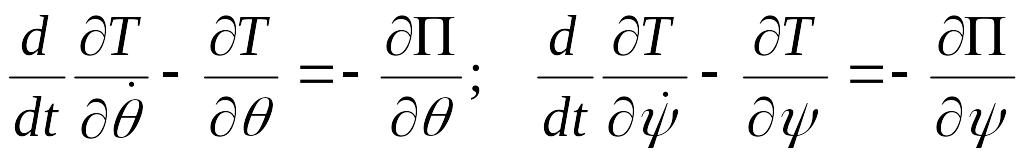2.Найти условие, при котором возможны стационарные движения по окружности (или относительные равновесия).

3.Вводя возмущения

_,

из уравнений Лагранжа для заданного получить уравнения возмущенного движения;

4. Выделить в уравнениях возмущенного движения линейные по члены.

Задача 2. Конический маятник (в переменных Рауса).

Постановка задачи: В коническом маятнике – циклическая координата , так как от нее не зависят ни кинетическая, ни потенциальная энергия, и непотенциальные обобщенные силы отсутствуют. Один из удобных способов описания динамики таких систем – применение переменных Рауса.

Требуется:

1. Ввести функцию Рауса 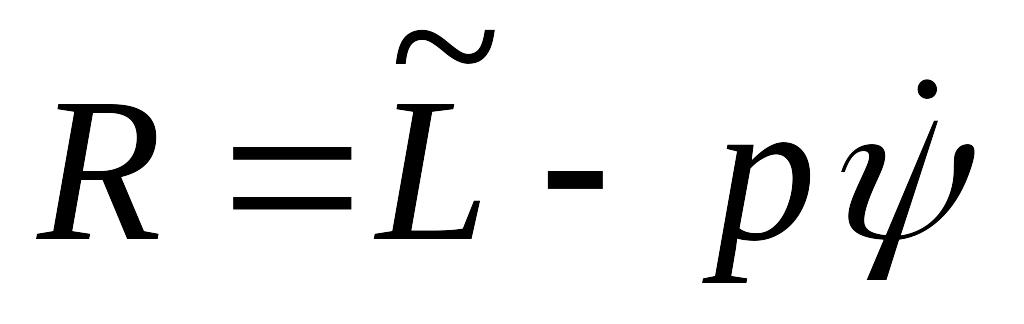, где 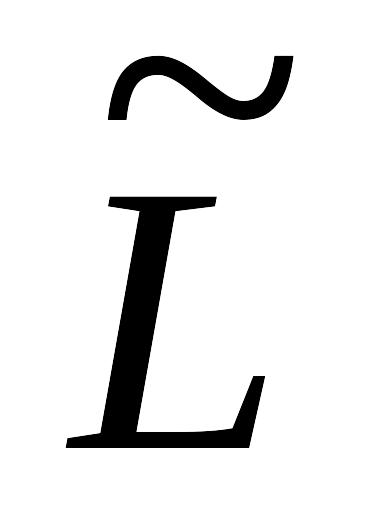– функция Лагранжа 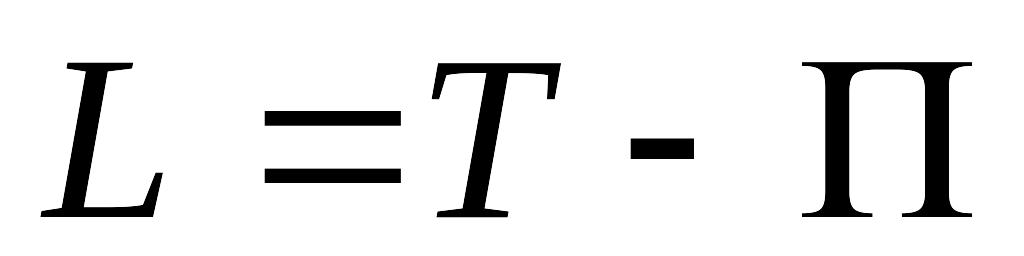, в которой циклическая скорость 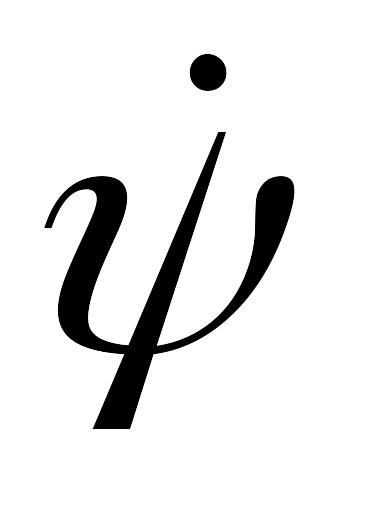заменена ее выражением из уравнения 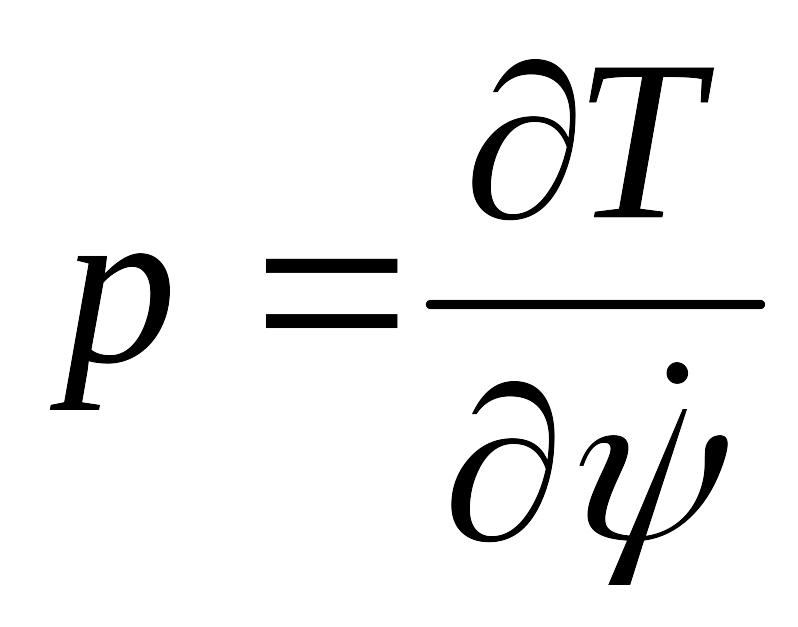(это же выражение подставляется и в произведение ).

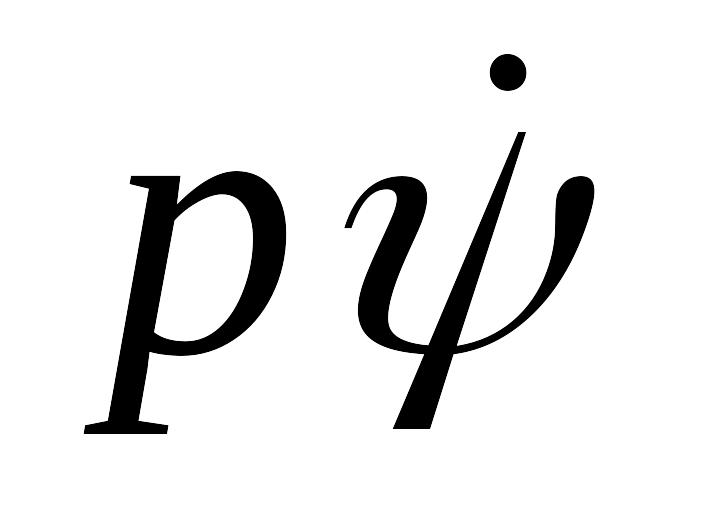2. Составить уравнения Рауса

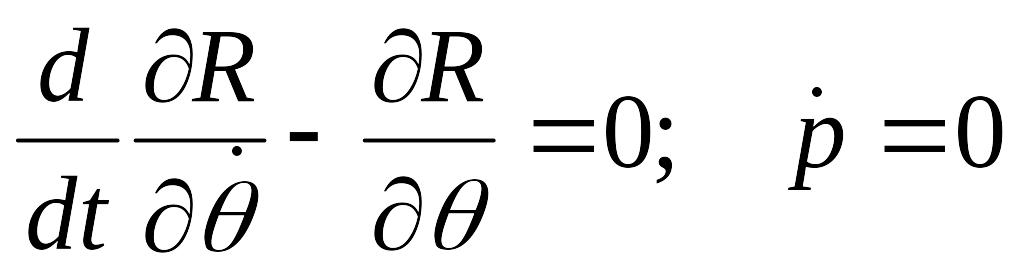
3. Найти условия существования стационарного движения

в переменных Рауса.

4. Вводя возмущения

получить из уравнений Рауса уравнения возмущенного движения для заданного угла . Выделить в этих уравнениях линейные члены.

Указание: значение угла для конкретного варианта индивидуального задания определяется выражением , где N – порядковый номер студента в списке группы.

Библиографический список

1. Ляпунов А.М. Собрание сочинений. В 2 т. Т. 2 / А.М. Ляпунов. – М.-Л. : Изд-во АН СССР, 1956.

2. Кильчевский Н.А. Курс теоретической механики. В 2 т. Т. 2. / Н.А. Кильчевский. – М.: Наука, 1977.

3. Демидович Б.П. Лекции по математической теории устойчивости / Б.П. Демидович. – М .: Наука, 1967.

4. Румянцев В.В. Устойчивость и стабилизация по отношению к части переменных. / В.В. Румянцев, А.С. Озиранер. – М. : Наука. 1987.

5. Малкин И.Г. Теория устойчивости движения. / И.Г. Малкин. – М. : Наука. 1966.

6. Меркин Д.Р. Введение в теорию устойчивости движения. / Д.Р. Меркин. – М. : Наука. 1976.

7. Барбашин Е.А. Функции Ляпунова. / Е.А. Барбашин. – М. : Наука. 1970.

Учебное издание

Красинский Александр Яковлевич

Красинская Эсфира Мустафовна

КОМПЬЮТЕРНОЕ УПРАВЛЕНИЕ

МЕХАТРОННЫМИ СИСТЕМАМИ

Основные понятия теории устойчивости.

Приложение теории устойчивости к задачам управления.

Методические указания к выполнению курсовой работы

для студентов специальности 220401 – Мехатроника и направления подготовки бакалавров 221000 – Мехатроника и робототехника

Редактор И.А. Мырсина

Подписано в печать 25.04.11. Усл. печ. л. 1,5. Тираж 30 экз.

Заказ . Изд. № 41.

МГУПБ. 109316. Москва, ул. Талалихина, 33.

ООО «Франтера». 109316. Москва, ул. Талалихина, 33.

25