4. Уравнения возмущенного движения [3, 5, 6]

Проведем в системе (3) замену переменных . В новых переменных будем иметь

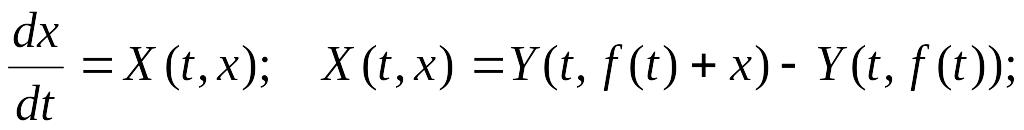(12)

причем .

Система (12) определяет дифференциальные уравнения возмущенного движения. Движение при такой замене переходит в положение равновесия системы (12).

Исследование устойчивости по первому приближению.

Для исследования устойчивости отдельного решения нелинейной системы можно составить уравнения возмущенного движения, выделить в них первое приближение. Если рассматриваются автономные системы (время явно не входит в правые части), то затем можно воспользоваться следующими теоремами А.М.Ляпунова об асимптотической устойчивости и неустойчивости по первому приближению:

Теорема 1. Если все корни характеристического уравнения системы первого приближения уравнений возмущенного движения имеют отрицательные вещественные части, то невозмущенное движение устойчиво асимптотически при любых нелинейных членах полных уравнений возмущенного движения.

Теорема 2. Если хотя бы один корень характеристического уравнения системы первого приближения уравнений возмущенного движения имеет положительную вещественную часть, то невозмущенное движение неустойчиво при любых нелинейных членах полных уравнений возмущенного движения.

При исследовании устойчивости по первому приближению неасимптотическая устойчивость для нелинейных систем может иметь место только в критических по Ляпунову случаях, когда вещественные части некоторых корней характеристического уравнения обращаются в нуль, а остальные его корни имеют отрицательные вещественные части.

В таких случаях нельзя получить достаточные условия устойчивости по первому приближению, рассмотрение первого приближения недостаточно для полного решения вопроса об устойчивости. Но в этих случаях можно получить необходимые условия устойчивости – условия, при нарушении которых движение становится неустойчивым. Это условия, при которых отсутствуют корни характеристического уравнения системы первого приближения с положительными вещественными частями.

В критических случаях достаточные условия устойчивости можно получить с помощью метода функций Ляпунова, а также с помощью специальной теории критических случаев[1, 5].

5. Метод функций ляпунова [5, 6]

Как отмечает А.М.Ляпунов «…Все наиболее интересные и важные вопросы механики (как, например, те, которые приводят к каноническим уравнениям) таковы, что в особенных случаях, когда первое приближение недостаточно, задача делается для них в высшей степени трудною. И пока невозможно указать каких-либо приемов для ее решения. Случаи этого рода весьма разнообразны, и в каждом из них задача получает свой особый характер, так что не может быть и речи о каких-либо общих методах ее решения, которые относились бы ко всем таким случаям. Известно, что существуют случаи, когда рассматриваемая задача допускает приведение к некоторой задаче о максимумах . . . Всем известна теорема Лагранжа об устойчивости равновесия . . . и изящное доказательство, предложенное для нее Лежен Дирихле. Последнее основывается на соображениях, которые могут послужить для доказательства многих подобных теорем » [1].

Руководствуясь такими соображениями, А.М. Ляпунов разработал так называемый второй метод исследования устойчивости - метод функций Ляпунова. Метод функций Ляпунова, еще называемый прямым методом – один из наиболее эффективных методов решения задач устойчивости. А.М.Ляпунов предложил, не отыскивая решений уравнений возмущенного движения, строить некоторые функции, по изменению которых вдоль траекторий уравнений возмущенного движения можно делать вывод об устойчивости невозмущенного движения.

Если заключение об асимптотической устойчивости делать по первому приближению, то в силу доказательства теоремы Ляпунова об устойчивости по первому приближению мы можем утверждать, что невозмущенное движение будет асимптотически устойчиво только при малых начальных отклонениях (так называемая «устойчивость в малом»). Множество точек, притягиваемых при к невозмущенному движению, т.е. область притяжения, может оказаться весьма ограниченной. Но область притяжения в действительности может быть и большой, только оценки, получаемые при исследовании по первому приближению, дают почти непригодные с точки зрения практики результаты.

Поэтому даже в тех случаях, когда устойчивость можно установить по первому приближению, построение функции Ляпунова поможет дать хорошую оценку области притяжения, оценку решения, т.е. переходного процесса, и оценку времени переходного процесса.

«Заметим, что для всякой системы дифференциальных уравнений любая определенно-положительная функция может служить функцией Ляпунова . . . Требуя, чтобы в силу данной системы производная по времени от этой функции была знакоотрицательной, можно выписать какие-то условия устойчивости нулевого решения системы. При неосторожном выборе функции Ляпунова эти условия могут оказаться противоречивыми. Кроме того, если встать на такой путь рассуждений, мы неизбежно утонем в океане малоценных достаточных условий устойчивости, весьма далеких от того, чтобы быть необходимыми. Хорошо проверенным критерием оценки полученной функции Ляпунова является следующее требование: достаточные условия, полученные с помощью этой функции в нелинейном случае (для полной системы), должны быть необходимыми в линейном случае» [7] (полученными по первому приближению).