
- •Введение
- •1. Устойчивость по ляпунову
- •Основные определения
- •Постановка а.М.Ляпуновым задачи об устойчивости
- •2. Различные определения устойчивости решений
- •Дифференциальных уравнений.
- •4. Уравнения возмущенного движения [3, 5, 6]
- •5. Метод функций ляпунова [5, 6]
- •6. Метод функций ляпунова для автономных систем
- •Геометрическая интерпретация знакоопределенных функций
- •Теоремы о неустойчивости движения
- •Замечание о знакоопреденности функций.
- •Контрольные задания
- •Библиографический список
6. Метод функций ляпунова для автономных систем
Рассмотрим некоторые вещественные однозначные, непрерывные вместе с производными в области
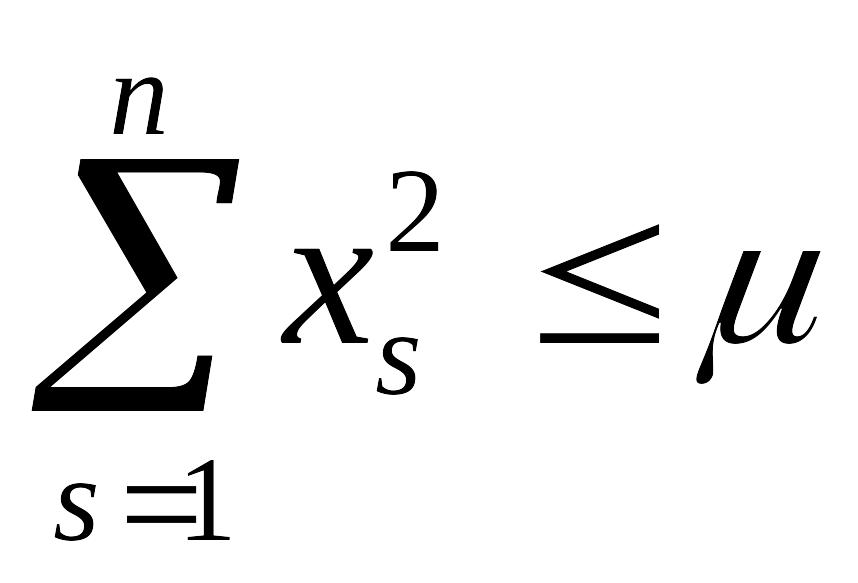 (13)
(13)
функции
![]() ,
причем
,
причем
![]() .
.
Определение
9.
Функция
![]() называется знакопостоянной (положительной
или отрицательной) в области (13), если
во всех точках области она принимает
значения только одного знака (нулевое
значение она может принимать не только
в начале координат).
называется знакопостоянной (положительной
или отрицательной) в области (13), если
во всех точках области она принимает
значения только одного знака (нулевое
значение она может принимать не только
в начале координат).
Определение 10. Функция называется знакоопределенной (определенно-положительной) в области (13) , если во всех точках области, кроме начала координат, она принимает значения строго только одного знака (больше нуля).
Примеры:
![]() функция знакопостоянная положительная,
так как она обращается в нуль не только
в начале координат, но и на прямой
функция знакопостоянная положительная,
так как она обращается в нуль не только
в начале координат, но и на прямой
![]() .
.
Функция![]() в пространстве трех переменных является
знакоположительной: она равна нулю не
только в начале координат, но и на прямой
в пространстве трех переменных является
знакоположительной: она равна нулю не
только в начале координат, но и на прямой
![]() .
В пространстве же двух переменных
.
В пространстве же двух переменных
![]() эта функция является
определенно-положительной.
эта функция является
определенно-положительной.
Геометрическая интерпретация знакоопределенных функций
Поверхности
уровня
![]() знакоопределенной функции по крайней
мере для достаточно малых
С замкнуты.
Действительно, рассмотрим такую
поверхность. Для определенности
предположим, что
положительно-определенная функция
(С - положительное число). При С=0 будем
иметь
знакоопределенной функции по крайней
мере для достаточно малых
С замкнуты.
Действительно, рассмотрим такую
поверхность. Для определенности
предположим, что
положительно-определенная функция
(С - положительное число). При С=0 будем
иметь
![]() ,
откуда
,
откуда
![]() ,
т.е. поверхность
,
т.е. поверхность
![]() вырождается в точку. Пусть l
– точный нижний предел функции
на границе области (13). Очевидно l
>0.
Если рассмотрим произвольную непрерывную
кривую, выходящую из начала координат
к границе области (13) и проследим за
изменением функции
вдоль этой кривой, то получим, что в
начале кривой
,
а в конце
вырождается в точку. Пусть l
– точный нижний предел функции
на границе области (13). Очевидно l
>0.
Если рассмотрим произвольную непрерывную
кривую, выходящую из начала координат
к границе области (13) и проследим за
изменением функции
вдоль этой кривой, то получим, что в
начале кривой
,
а в конце
![]() .
Следовательно , в некоторой точке этой
кривой
.
Следовательно , в некоторой точке этой
кривой
![]() необходимо принимает значение С ,
если только С<l
, так как предполагается, что функция
Ляпунова непрерывна и определена во
всех точках области (13). Значит, поверхности
для С<l
будут замкнуты и окружают начало
координат.
необходимо принимает значение С ,
если только С<l
, так как предполагается, что функция
Ляпунова непрерывна и определена во
всех точках области (13). Значит, поверхности
для С<l
будут замкнуты и окружают начало
координат.
Если
взять поверхности![]() ,
,
![]() ,
... ,
,
... ,
![]() ,
причем
,
причем
![]() , то поверхности расположатся следующим
образом.
, то поверхности расположатся следующим
образом.
![]()
![]()
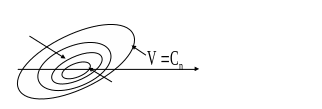
Производной по времени от функции Ляпунова в силу уравнений возмущенного движения (12) называется выражение
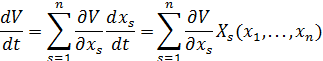 (14)
(14)
Такая производная характеризует изменение функции V вдоль траектории уравнений возмущенного движения.
В основе исследования устойчивости методом функций Ляпунова лежат следующие теоремы [5, 6, 7].
Теорема Ляпунова об устойчивости: если для дифференциальных уравнений возмущенного движения можно найти знакоопределенную функцию
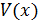 ,
производная которой
,
производная которой
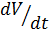 в силу этих уравнений была бы
знакопостоянной функцией противоположного
с
в силу этих уравнений была бы
знакопостоянной функцией противоположного
с  знака, то невозмущенное движение
устойчиво.
знака, то невозмущенное движение
устойчиво.
Замечание. Если в качестве функции Ляпунова взять полную энергию системы, то из этой теоремы легко установить справедливость теоремы Лагранжа об устойчивости равновесия: положение равновесия консервативной механической системы устойчиво, если для него потенциальная энергия имеет строгий локальный минимум.
Теорема Ляпунова об асимптотической устойчивости: если для дифференциальных уравнений возмущенного движения можно найти знакоопределенную функцию , производная которой в силу этих уравнений была бы знакоопределенной функцией противоположного с знака, то невозмущенное движение устойчиво асимптотически.
Т
 еорема
Барбашина - Красовского об асимптотической
устойчивости:
если для дифференциальных уравнений
возмущенного движения можно найти
определенно-положительную функцию
такую, что ее производная в силу этих
уравнений
удовлетворяет в области (13) условию:
еорема
Барбашина - Красовского об асимптотической
устойчивости:
если для дифференциальных уравнений
возмущенного движения можно найти
определенно-положительную функцию
такую, что ее производная в силу этих
уравнений
удовлетворяет в области (13) условию:
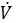 знакоотрицательна,
причем многообразие К точек, для которых
знакоотрицательна,
причем многообразие К точек, для которых
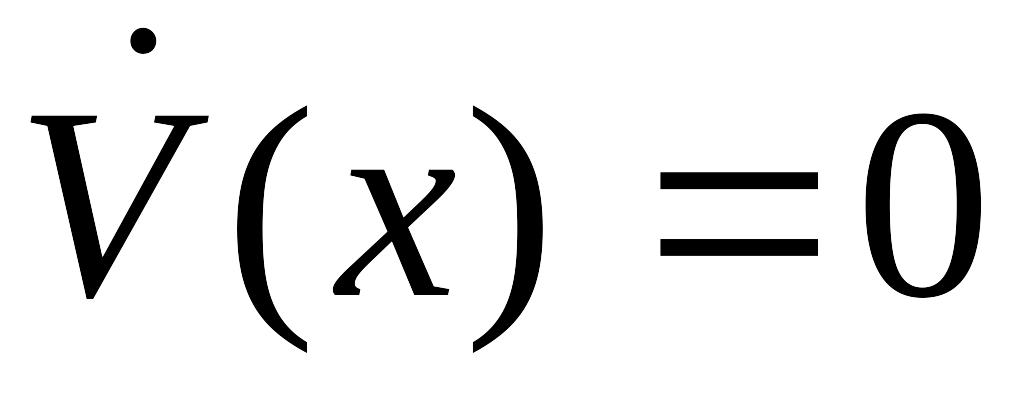 ,
не содержит целых траекторий системы,
кроме начала координат при
,
не содержит целых траекторий системы,
кроме начала координат при 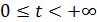 ,
то невозмущенное движение асимптотически
устойчиво.
,
то невозмущенное движение асимптотически
устойчиво.
К






Замечание об устойчивости регулируемых систем. Во многих технических задачах важно, чтобы невозмущенное движение было асимптотически устойчивым и чтобы эта устойчивость имела место при любых начальных возмущениях (асимптотически устойчиво в целом). При этом дело сведется к построению функции Ляпунова, удовлетворяющей условиям следующих теорем Барбашина - Красовского об устойчивости в целом.
Теорема
1.
Если для дифференциальных уравнений
возмущенного движения возможно найти
определенно-положительную функцию
Ляпунова, полная производная по времени
которой, составленная в силу этих
уравнений, есть при всех
функция определенно-отрицательная и
если при этом
![]() ,
то невозмущенное движение асимптотически
устойчиво в целом.
,
то невозмущенное движение асимптотически
устойчиво в целом.
Теорема 2. Если для дифференциальных уравнений возмущенного движения можно найти такую определенно-положительную функцию, что она удовлетворяет условию и производная которой в силу этих уравнений, знакоотрицательна, причем многообразие точек, для которых , не содержит целых траекторий системы, кроме начала координат при , то невозмущенное движение асимптотически устойчиво в целом.
