1.2.Выборочная средняя.

Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема n.

Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.

Если все значения признака выборки различны, то

если же все значения имеют частоты n1, n2,…,nk, то

Выборочная средняя является несмещенной и состоятельной оценкой генеральной средней.

Замечание: Если выборка представлена интервальным вариационным рядом, то за xi принимают середины частичных интервалов.

.4.Выборочная дисперсия.

Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения , вводят сводную характеристику- выборочную дисперсию.

Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

Если все значения признака выборки различны, то

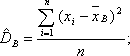
если же все значения имеют частоты n1, n2,…,nk, то

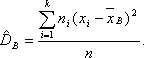
1. Условные варианты.

Предположим, что варианты выборки расположены в возрастающем порядке, т.е. в виде вариационного ряда.

Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью .

Условными называют варианты, определяемые равенством , где – ложный нуль (новое начало отсчета); – шаг, т.е. разность между любыми двумя соседними первоначальными вариантами (новая единица масштаба).

Упрощенные методы расчета сводных характеристик выборки основаны на замене первоначальных вариант условными.

Покажем, что если вариационный ряд состоит из равноотстоящих вариант с шагом , то условные варианты есть целые числа. Действительно, выберем в качестве ложного нуля произвольную варианту, например .

Тогда .

Так как и - целые числа, то их разность - также целое число.

Начальным эмпирическим моментом порядка называют обычный момент порядка при .

В частности,

т.е. начальный эмпирический момент первого порядка равен выборочной средней.

Центральным эмпирическим моментом порядка называют обычный момент порядка при

.

Исправленная дисперсия.

Выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно

Для исправления выборочной дисперсии достаточно умножить ее на дробь

получим исправленную дисперсию S2. Исправленная дисперсия является несмещенной оценкой.

т.е. центральный эмпирический момент второго порядка равен выборочной дисперсии.

Метод произведений дает удобный способ вычисления условных элементов различных порядков вариационного ряда с равноотстоящими вариантами. Зная же условные моменты, нетрудно найти интересующие нас начальные и центральные эмпирические моменты. В частности, методом произведений удобно вычислять выборочную среднюю и выборочную дисперсию. Целесообразно пользоваться расчетной таблицей, которая составляется так:

1) в первый столбец таблицы записывают выборочные (первоначальные ) варианты, располагая их в возрастающем порядке;

2) во второй столбец записывают частоты вариант; складывают все частоты и их сумму (объем выборки n) помещают в нижнюю клетку столбца;

3) в третий столбец записывают условные варианты , причем в качестве ложного нуля С выбирают варианту, которая расположена примерно в середине вариационного ряда, и полагают h равным разности между любыми двумя соседними вариантами; практически же третий столбец заполняется так: в клетке строки, содержащей выбранный ложный нуль, пишут 0; в клетках над нулем пишут последовательно -1, -2, -3 и т.д., а под нулем -1, 2, 3 и т.д.;

4) умножают частоты на условные варианты и записывают их произведения в четвертый столбец; сложив все полученные числа, их сумму помещают в нижнюю клетку столбца;

5) умножают частоты на квадраты условных вариант и записывают их произведения в пятый столбец; сложив все полученные числа, их сумму помещают в нижнюю клетку столбца;

6) умножают частоты на квадраты условных вариант, увеличенных каждая на единицу, и записывают произведения в шестой контрольный столбец; сложив все полученные числа, их сумму помещают в нижнюю клетку столбца.

После того, как расчетная таблица заполнена и проверена правильность вычислений, вычисляют условные моменты:

, .

Наконец, вычисляют выборочные среднюю и дисперсию по формулам (*) и :

,

Свойства оценок. Состоятельные оценки. Несмещенные оценки.

Для установления качества оценки используют три основные свойства и рассматривают несмещенные оценки, состоятельные оценки и эффективные оценки.

Для того, чтобы определить эти свойства, необходимо предварительно ввести понятие статистики. Под статистикой будем понимать функцию от выборки случайной величины . Следует отметить, что функция сама является случайной величиной. Если статистика позволяет оценить некоторую характеристику случайной величины , то говорят, что статистика оценивает . Например, статистика, оценивающая дисперсию случайной величины имеет вид:

.

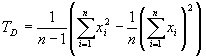
Статистика называется несмещенной оценкой параметра , если математическое ожидание оценки равняется оцениваемому параметру:

Статистика называется эффективной оценкой параметра , если среднеквадратическая ошибка данной оценки является наименьшей среди всех возможных оценок:

Статистика называется состоятельной оценкой параметра параметра , если с ростом размера выборки оценка стремиться по вероятности к оцениваемому параметру:

при любом сколь угодно малом

3)доверительный интервал (различные способы вычисления через распределение Стъюдента, через нормальное распределение, интервальная оценка матожидания при известном и неизвестном , точность и доверительная вероятность,

Доверительный интервал

, где t(p,f) - коэффициент Стьюдента при заданной доверительной вероятности p (обыно принимается значение 95%) и числе степеней свободы f.

• тоже распределены по нормальному закону:

Величина - это доверительный интервал, который используется в аналитической химии для оценки воспроизводимости.

http://apollyon1986.narod.ru/docs/TViMS/NP/lekziitv/lekziya13.htm#2.1.1. Доверительный интервал для оценки математического ожидания при известном s.

Надежностью (доверительной вероятностью)оценки Θ* параметра Θ называется вероятность γ того, что выполняется неравенство | Θ* - Θ | < δ

Доверительным называется интервал, в который попадает неизвестный параметр с заданной надежностью γ.

если для оценки Θ* некоторого параметра Θ справедливо неравенство | Θ* - Θ | < δ, число δ > 0 характеризует точность оценки ( чем меньше δ, тем точнее оценка).