1) Уровня линии (поверхности), множества точек, в которых функция и (Р) точки Р плоскости (пространства) принимает постоянные значения.Уравнение u (P) = const в двумерной области определяет линию (линию уровня), в трёхмерной области √ поверхность (поверхность уровня). Изображение функций с помощью У. л. (п.) широко применяется в метеорологии (изотермы, изобары и т.д.), геодезии и топографии (горизонтали) и др. науках. У. л.(п.) в точках экстремума функции и (Р) вырождаются в точки. Градиент функции u (Р) перпендикулярен У. л. (п.) в соответствующей точке.

2)  Предел и непрерывность функции нескольких переменных.

 

Введем понятие δ-окрестности точки М₀ (х₀ , у₀) на плоскости Оху как круга радиуса δ с центром в данной точке. Аналогично можно определить δ-окрестность в трехмерном пространстве как шар радиуса δ с центром в точке М₀ (х₀ , у₀ , z₀). Для n-мерного пространства будем называть δ-окрестностью точки М₀ множество точек М с координатами  , удовлетворяющими условию

                   

где   - координаты точки М₀. Иногда это множество называют «шаром» в n-мерном пространстве.

Определение 1.4. Число А называется пределом функции нескольких переменных f в точке М₀, если        такое, что | f(M) – A| < ε для любой точки М изδ-окрестности М₀.

Обозначения:    .

Необходимо учитывать, что при этом точка М может приближаться к М₀, условно говоря, по любой траектории внутри δ-окрестности точки М₀. Поэтому следует отличать предел функции нескольких переменных в общем смысле от так называемых повторных пределов, получаемых последовательными предельными переходами по каждому аргументу в отдельности.

 

Примеры.

1. Покажем, что функция     не имеет предела при М→О(0,0). Действительно, если в качестве линии, по которой точка М приближается к началу координат, выбрать прямую у = х, то на этой прямой  . Если же траекторией движения считать прямую у = 2х, то  . Следовательно, предел в точке (0,0) не существует.

2. Найдем повторные пределы функции    при х→0, у→0.  ,   . Если же произвести предельные переходы в обратном порядке, получим:      Таким образом, повторные пределы оказались различными (откуда следует, конечно, что функция не имеет в точке (0,0) предела в обычном смысле).

 

Замечание. Можно доказать, что из существования предела в данной точке в обычном смысле и существования в этой точке пределов по отдельным аргументам следует существование и равенство повторных пределов. Обратное утверждение неверно.

 

Определение 1.5. Функция f  называется непрерывной в точке М₀ , если                    (1.2)

Если ввести обозначения  , то условие (1.2) можно переписать в форме                                            (1.3)

Определение 1.6. Внутренняя точка М₀ области определения функции  z = f (M) называется точкой разрыва функции, если в этой точке не выполняются условия (1.2), (1.3).

Замечание. Множество точек разрыва может образовывать на плоскости или в пространстве линии или поверхности разрыва.

Примеры.

1. Функция  z = x² + y² непрерывна в любой точке плоскости Оху. Действительно,  , поэтому  .

2. Единственной точкой разрыва функции   является точка (0,0).

3. Для функции   линией разрыва является прямая  х + у = 0.

 

         Свойства пределов и непрерывных функций.

 

Так как определения предела и непрерывности для функции нескольких переменных практически совпадает с соответствующими определениями для функции одной переменной, то для функций нескольких переменных сохраняются все свойства пределов и непрерывных функций, доказанные в первой части курса, а именно:

1)      Если существуют  то существуют и   (если  ).

2)      Если   а  и для любого i существуют пределы   и существует  , где М₀  , то существует и предел сложной функции  при  , где  - координаты точки Р₀.

3)      Если функции f(M) и g(M) непрерывны в точке М₀, то в этой точке непрерывны и функции f(M) + g(M), kf(M), f(M)•g(M), f(M)/g(M) (если g(M₀) ≠ 0).

4)      Если функции  непрерывны в точке Р₀  , а функция  непрерывна в точке М₀ , где  , то сложная функция   непрерывна в точке Р₀.

5)      Функция   непрерывная в замкнутой ограниченной области D, принимает в этой области свое наибольшее и наименьшее значения.

6)      Если функция   непрерывная в замкнутой ограниченной области D, принимает в этой области значения А и В, то она принимает в области D и любое промежуточное значение, лежащее между А и В.

7)      Если функция   непрерывная в замкнутой ограниченной области D, принимает в этой области значения разных знаков, то найдется по крайней мере одна точка из области D, в которой f = 0.

 

 

3)   Пусть f(x, y) — функция двух переменных x, y, определена в некоторой окрестности точки (x₀, y₀). Если существует конечный предел  ,то функция f(x, y) имеет в точке (x₀, y₀ ) частную производную по переменной x. Аналогично определяется частная производная функции f(x₁, x₂, …, x_n) по переменной x_i :  Обозначают: ,

При рассмотрении функции z=f(x,y) двух переменных мы уже рассматривали частные приращения. Мы можем найти предел отношения частного приращения к соответствующему приращению аргумента.

Определение.

Частной производной функции z=f(x,y) по аргументу x называется предел отношения частного приращения функции к соответствующему приращению аргумента Dx, когда DxÞ0.

,                       (2-115)

аналогично и по переменной y

,                         (2-116)

кроме того, частные производные могут обозначаться как:

.

При вычислении частных производных по одной из переменных вторая переменная считается постоянной.

Пример 1 

z=x²×sin(y) Þ  2x×sin (y).    x²×cos (x).

Пример 2.

 ) Þ  ;  .

Замечание:

частные производные могут вычисляться для всех независимых переменных функции нескольких переменных.

Можно предположить, что функции, получаемые в результате дифференцирования по одной из переменных, тоже будут являться функциями нескольких переменных.

Определение: частная производная от частной производной функции называется частной производной второго порядка.

Таких частных производных второго порядка для функции двух переменных будет уже четыре:

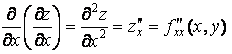. Функция два раза подряд дифференцируется по x;

                                     (2-117)

здесь дифференцируется сначала по x затем по y ;

                                      (2-118)

функция два раза подряд дифференцируема по y;

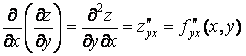                                   (2-119)

функция дифференцируема сначала по y, затем по x.

Частные производные находят по правилам и формулам, аналогично формулам для обычных производных. Надо только помнить, по какой производной проводится дифференцирование, считать эту величину изменяющейся, а остальные - постоянными.

Пример.

Найти частные производные второго порядка от функции

z=x³·y²+2·y-6·x+1 Þ z’_x=3x²y²-6; z^’_y=2x³y+2; z”_xx =6xy²; =6x²y; z^”_yy=2x³; z^”_yx=6x²y.

Как видим,  . Таково общее свойство смешанных производных.

Частные производные

Определение. Пусть в некоторой области задана функция z = f(x, y). Возьмем произвольную точку М(х, у) и зададим приращение Dх к переменной х. Тогда величина Dxz = f( x + Dx, y) – f(x, y) называется частным приращением функции по х.

Можно записать

.

 

Тогда   называется частной производной функции z = f(x, y) по х. Обозначение: 

Аналогично определяется частная производная функции по у.

Геометрическим смыслом частной производной (допустим  ) является тангенс угла наклона касательной, проведенной в точке N0(x0, y0, z0) к сечению поверхности плоскостью у = у0.

Полное приращение и полный дифференциал

Определение. Для функции f(x, y) выражение Dz = f( x + Dx, y + Dy) – f(x, y) называется полным приращением.

Определение. Выражение   называется полным приращением функции f(x, y) в некоторой точке (х, у), где a1 и a2 – бесконечно малые функции при Dх -> 0 и Dу -> 0 соответственно.

Определение: Полным дифференциалом функции z = f(x, y) называется главная линейная относительно Dх и Dу приращения функции Dz в точке (х, у).

Для функции произвольного числа переменных:

Частные производные высших порядков

Если функция f(x, y) определена в некоторой области D, то ее частные производные   и   тоже будут определены в той же области или ее части.  Будем называть эти производные частными производными первого порядка. Производные этих функций будут частными производными второго порядка.

    Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.

Определение. Частные производные вида     и т.д. называются смешанными производными.

4) Пусть на области D задана функция двух переменных z =f(х,у),M₀(x₀;y₀) - внутренняя точка области D, M(x₀+Δx;y+Δy) - "соседняя" с M₀ точка из D.

Рассмотрим полное приращение функции:

Если Δz представлено в виде:

где A, B - постоянные (не зависящие от Δx, Δy),   - расстояние междуM и M₀, α(Δx,Δy) - бесконечно малая при Δx   0, Δy  0; тогда функция z =f(х,у) называется дифференцируемой в точке M₀, а выражение

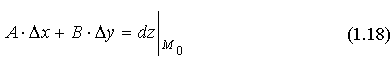
называется полным дифференциалом функции z =f(х;у) в точке M₀.

Теорема 1.1. Если z =f(х;у) дифференцируема в точке M₀, то

Доказательство

Так как в (1.16) Δx, Δy - произвольные бесконечно малые, то можно взять Δy =0, Δx≠0, Δx  0, тогда

после чего из (1.16) следует

Тогда

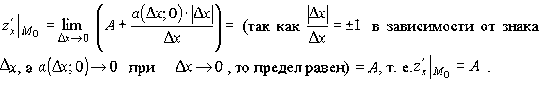
Аналогично доказывается, что

и теорема 1.1. доказана.

Замечание: из дифференцируемости z =f(х,у) в точке M₀ следует существование частных производных. Обратное утверждение неверно (из существования частных производных в точкеM₀ не следует дифференцируемость в точке M₀ ).

В итоге, с учётом теоремы 1.1 формула (1.18) примет вид:

Следствие. Функция, дифференцируемая в точке M₀, непрерывна в этой точке (так как из (1.17) следует, что при Δx   0, Δy   0: Δz   0, z(M)   z(M0)).

Замечание: Аналогично для случая трех и более переменных. Выражение (1.17) примет вид:

где

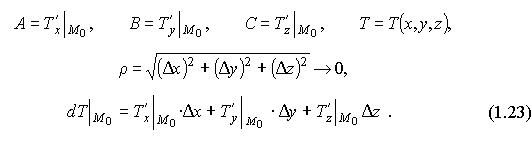
Используя геометрический смысл (рис.1.3) частных производных   и  можно получить следующее уравнение (1.24) касательной плоскости π_касs к поверхности: z =f(х,у) в точке C₀(x₀,y₀,z₀), z₀=z(M):

Из сравнения (1.24) и (1.21) получаем геометрический смысл полного дифференциала функции двух переменных:

- приращение аппликаты z при движении точки С по касательной плоскости из точки С0 в точку

где   находится из (1.24).

Уравнение нормали Lн к поверхности: z =f(х,у) в точке С0 получается, как уравнение прямой, проходящей через С₀ перпендикулярно к касательной плоскости: