Основные определения.

1. Основные модели:

1)Мальтуса (по экспоненете),

2)Ферхюльста-Перла,

3) модели Вольтерра

А) межвидовой конкуренции,

В) хищник-жертва

С) кооперации видов

4) теория наследственности (простые вероятностные модели, комбинаторика)

2. Определение вероятности (классическое, статистическое,геометрическое, аксиоматический подход).

3. Правила сложения и умножения вероятностей (совместные, несовместные, зависимые, независимые события).

4. Комбинаторика (перестановки, размещения, число сочетаний).

5. Формула полной вероятности, формула Байеса.

6. Повторные испытания, формула Бернулли.

7. Случайная величина (дискретная непрерывная)

8. Законы распределения: ряд распределения, функция распределения, плотность распределения.

9. Числовые параметры распределения ( матожидание, дисперсия, начальные и центральные моменты).

10. Основные законы распределения случайных величин:

Биномиальное, геометрическое, гипергеометрическое, Пуассона(дискр.), равномерное, показательное, нормальное, Стъюдента, Хи-квадрат(непрер.).

11. Статистика:

1)Генеральная совокупность, выборочная совокупность, размах, вариационный ряд, варианты, частота, относительная частота, полигон, гистограмма, плотность частоты,

2)точечные оценки параметров распределения, выборочная средняя, выборочная дисперсия, метод произведений, условная варианта, условные моменты первого и второго порядка, исправленная дисперсия, свойства оценок ( состоятельность, несмещенность, эффективность),

3)доверительный интервал (различные способы вычисления через распределение Стъюдента, через нормальное распределение, интервальная оценка матожидания при известном и неизвестном , точность и доверительная вероятность,

4)метод моментов,

5)проверка гипотез, метод -квадрат, ошибки 1-го и второго рода , уровень значимости, - гипотеза, - гипотеза.

6) поле корреляции (форма и теснота корреляционной связи), эмпирическая линия регрессии, линейная регрессия обусловленная двумерным нормальным законом распределения, метод наименьших квадратов, система нормальных уравнений.

Ответы:

12. 1. Основные модели:

1)Мальтуса (по экспоненете),

2)Ферхюльста-Перла,

3) модели Вольтерра

А) межвидовой конкуренции,

В) хищник-жертва

С) кооперации видов

1.Уравнения экспоненциального роста. ( ; )

Уравнение экспоненциального роста.

Второй всемирно известной математической моделью, в основу которой положена задача о динамике численности популяции, является классическая модель неограниченного роста - геометрическая прогрессия в дискретном представлении,

или экспонента, - в непрерывном dx – новые особи; dt – промежуток времени, за который образовалась начальная численность - x ; r- биотический потенциал

Модель предложена Мальтусом в 1798 г. в его классическом труде "О росте народонаселения". Томас Роберт Мальтус (1766-1834) известный английский демограф и экономист, обратил внимание на тот факт, что численность популяции растет по экспоненте (в геометрической прогрессии), в то время как производство продуктов питания растет со временем линейно (в арифметической прогрессии), из чего сделал справедливый вывод, что рано или поздно экспонента обязательно "обгонит" линейную функцию, и наступит голод.

Обсуждению важности вывода Мальтуса для популяционной динамики Дарвин посвятил несколько страниц своего дневника, указывая, что поскольку ни одна популяция не размножается до бесконечности, должны существовать факторы, препятствующие такому неограниченному размножению. Среди этих факторов может быть нехватка ресурса (продовольствия), вызывающая конкуренцию внутри популяции за ресурс, хищничество, конкуренция c другими видами. Результатом является замедление скорости роста популяции и выход ее численности на стационарный уровень.

, при r=const, (r = b - d Удельная скорость популяционного роста как разность удельной рождаемости и удельной смертности; b – удельная рождаемость d – удельная смертность)

r > 0, численность растёт

r < 0, численность падает

r = 0, численность остается неизменной;

Экспоненциальный рост называют логарифмическим. Уравнение экспоненциального роста в логарифмической форме имеет следующий вид: lnxt = lnx0 + rt, т. е., по сути, это просто уравнение прямой, причем коэффициент r характеризует угол наклона ее к осям.

1.2 Ферхюльста-Перла. Из этого можно вывести, уравнение Ферхюльста. Оно описывает динамику роста численности популяции, и представляет собой нелинейное уравнение следующего вида: . Где xn - численность популяции через n лет, xn+1 - на последующий год, r - параметр роста. Первое выражение в правой части уравнения - равно приросту численности популяции, а второе - ее убыли Исходные предположения для вывода уравнения при рассмотрении популяционной динамики выглядят следующим образом:

скорость размножения популяции пропорциональна её текущей численности, при прочих равных условиях

скорость размножения популяции пропорциональна количеству доступных ресурсов, при прочих равных условиях. Таким образом, второй член уравнения отражает конкуренцию за ресурсы, которая ограничивает рост популяции.

Обозначая через численность популяции (в экологии часто используется обозначение ), а время — , модель сводится к дифференциальному уравнению:

.1.3 Модели Лотки-Вольтерра. Мдели Лотки-Вольтерра, активно применяются биологами для изучения взаимодействия популяций.

Проанализируем систему двух дифференциальных уравнений, описывающих взаимодействие двух популяций:

dx1 /dt = c1 x1 + a12 x1 x2 + a11 x1(2),

dx2/dt = c2 x2 + a21 x1 x2 + a22 x2(2), где x1 (t) и х2 (t) - численность популяций в момент t.

Линейные члены с1 x1 и с2 х2 в правых частях уравнений соответствуют свободному размножению видов. Если коэффициент ci > 0, то численность соответствующего вида растет (положительная обратная связь), если сi < 0, то численность уменьшается (отрицательная обратная связь).

Члены аii хi(2) отражают наличие внутривидовой конкуренции при а.. < 0. Если а.. > 0, то мы имеем дело с сильной положительной обратной связью, отражающей эффект "группирования",- благоприятное влияние на численность популяции процесса образования сообществ.

Наиболее интересны в этой модели произведения факторов x1 х2, отражающие процесс взаимодействия двух популяций. Если коэффициенты а., отрицательны, то виды конкурируют друг с другом. При аij > 0 процесс взаимодействия биологи называют симбиозом (в социальной сфере более уместно говорить о сотрудничестве, кооперации). Если a12 > 0 и a21 < 0, то первый вид является хищником, а второй - жертвой (если численность первого вида больше, то это взаимодействие паразита с хозяином).

УРАВНЕНИЯ МЕЖВИДОВОЙ КОНКУРЕНЦИИ предложенные А. Лоткой (1925) и В. Вольтеррой (1926, 1931) уравнения для математического анализа межвидовой конкуренции:

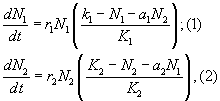, где N1 и N2 — численность двух конкурирующих между собой популяций в единицу времени (t = 1); r1, r2 — специфические потенциальные скорости конкурирующих популяций, обусловленные свойствами организма в нелимитирующих условиях среды; K1 и K2 — допустимые численности конкурирующих видов; а1 и a2 — коэффициенты конкуренции обоих видов.

"хищник-жертва". Пусть есть два биологических вида, которые совместно обитают в изолированной среде. Среда стационарна и обеспечивает в неограниченном количестве всем необходимым для жизни один из видов, который будем называть жертвой. Другой вид - хищник также находится в стационарных условиях, но питается лишь особями первого вида.

Это могут быть караси и щуки, зайцы и волки, мыши и лисы, микробы и антитела и т. д. ... Будем для определенности называть их карасями и щуками.

Караси и щуки живут в некотором изолированном пруду. Среда предоставляет карасям питание в неограниченном количестве, а щуки питаются лишь карасями.

Обозначим

у - число щук,

х - число карасей.

Со временем число карасей и щук меняется, но так как рыбы в пруду много, то не будем различать 1020 карасей или 1021 и поэтому будем считать х и у непрерывными функциями времени t.

Будем называть пару чисел (х, у) состоянием модели. Попробуем определить, как состояние меняется с течением времени.

Надо сказать, что в биологии дело обстоит значительно сложнее, чем, скажем, в механике, где само понятие состояния формализовано и существуют законы Ньютона, позволяющие описать изменение состояния. В биологии этого пока нет.

Попробуем из самых простых соображений найти, как меняется состояние (х, у).

Рассмотрим x' - скорость изменения численности карасей.

Если щук нет, то число карасей увеличивается и тем быстрее, чем больше карасей.

Будем считать, что эта зависимость линейная : x' 1 x, причем коэффициент 1 зависит только от условий жизни карасей, их естественной смертности и рождаемости.

Скорость изменения y' числа щук (если нет карасей), зависит от числа щук y.

Будем считать, что y'2 y . Если карасей нет, то число щук уменьшается (у них нет пищи) и они вымирают.

В экосистеме скорость изменения численности каждого вида также будем считать пропорциональной его численности, но только с коэффициентом, который зависит от численности особей другого вида. Так, для карасей этот коэффициент уменьшается с увеличением числа щук, а для щук увеличивается с увеличением числа карасей. Будем считать эту зависимость также линейной.

Тогда получим систему из двух дифференциальных уравнений:

x' = 1 x - 1 yx,

y' = - 2 y + 2xy.

Эта система уравнений и называется моделью Вольтерра-Лотки. Числовые коэффициенты 1, 1, 2, 2 называются параметрами модели. Очевидно, что характер изменения состояния (x, y) определяется значаниями параметров.

Изменяя параметры и решая систему уравнений модели можно исследовать закономерности изменения состояния экологической системы. Именно это позволит вам сделать наша модель, которая находит решение уравнения Вольтерра - Лотки и выводит кривые x(t) и y(t) на экран.

В качестве примера на рисунке построены кривые изменения численности карасейx и щук y в зависимости от времени t для некоторых типчных значений параметров.

Максимумы кривых чередуются, причем максимумы щук отстают от максимума карасей. Это отставание разное для разных экосистем типа "хищник - жертва", но, как правило, много меньше периода колебаний.

Несмотря на то, что рассмотренная модель является простейшей и в действительности все происходит много сложнее, она позволила объяснить кое-что из загадочного, что есть в природе. Перестали быть загадкой счастливые для рыболовов периоды, когда в водоеме оказывается громадное количество рыбы (из рисунка видно, что продолжаются они очнь недолго).