
- •4. Методи розв’язування задач для рівнянь в частинних похідних
- •5. Суть методу скінченних різниць (сіток). Елементарні відомості з теорії різницевих схем
- •5.1 Ідея методу скінченних різниць (сіток)
- •5.2 Елементарні поняття з теорії різницевих схем
- •6. Чисельне розв’язування крайових задач для рівнянь еліптичного типу
- •6.1 Апроксимація похідних (сіткова апроксимація)
- •6.2 Різницева апроксимація задачі Діріхле для рівнянь Лапласа та Пуассона
- •6.3 Чисельний метод розв’язування різницевої схеми (6.7), (6.8)
- •6.4 Алгоритм ручного рахунку задачі Діріхле
- •6.5 Деякі узагальнення методу скінченних різниць та його недоліки
- •7. Різницеві схеми для рівнянь теплопровідності
- •7.1 Явна різницева схема
- •7.1.1 Алгоритм ручного рахунку
- •7.2 Неявна різницева схема
- •7.2.1 Алгоритм ручного рахунку по неявній різницевій схемі
- •8.2.2 Різнецева схема з вагами
- •8.3 Різницеві схеми для рівняння теплопровідності із змінними коефіцієнтами
- •8.4 Різницеві схеми для нелінійного рівняння теплопровідності
- •9. Монотонні різницеві схеми для рівнянь параболічного типу, що містять перші похідні
- •9.1 Вступ
- •9.2 Монотонна рс для звичайного диф. Рівняння другого порядку, що містить першу похідну
- •9.3 Монотонна різницева схема для параболічного рівняння
- •10. Інтегро-інтерполяційний метод побудови рс
- •10.1 Вступ. Методи побудови рс
- •10.2 Приклади побудови рс інтегро-інтерполяційним методом
- •11. Різницеві схеми для рівнянь гіперболічного типу
- •11.1 Постановка задачі
- •11.2 Рс задачі.
- •12. Різницеві методи чисельного розв’язання багатовимірних задач математичної фізики. Різницева схема з вагами для двовимірного рівняння параболічного типу
- •12.1 Постановка задачі
- •12.2 Різницева схема задачі (12.1)-(12.3)
- •13. Економічні методи розв’язання крайових задач мат. Фізики
- •13.1 Вступ
- •13.2 Постановка задачі
- •Метод змінних напрямків
- •13.2 Стійкість поздовжньо-поперечної рс
- •14. Загальні відомості з теорії стійкості рс
- •14.1 Канонічний вигляд двохшарових рс
- •14.2 Теорема про стійкість по початкових даних
- •14.3 Сумарна апроксимація
- •14.4 Локально-одновимірна схема Самарського о.А.
- •15. Основи методу скінченних елементів чисельного розв’язування крайових задач математичної фізики
- •15.1 Вступ
- •15.2 Основна концепція мсе
- •15.3 Переваги і недоліки мсе
- •15.4 Математичні основи методу мсе
- •15.4.1. Постановка задачі.
- •15.4.2. Апроксимація базисними функціями.
- •15.4.3. Вибір параметрів .
- •1 5.4.4 Апроксимація за допомогою зважених нев’язок.
- •16. Кусково-визначені базисні функції і мсе
- •16.1 Поняття скінченого елемента
7.2.1 Алгоритм ручного рахунку по неявній різницевій схемі
Обчислити коефіцієнт температуропровідності
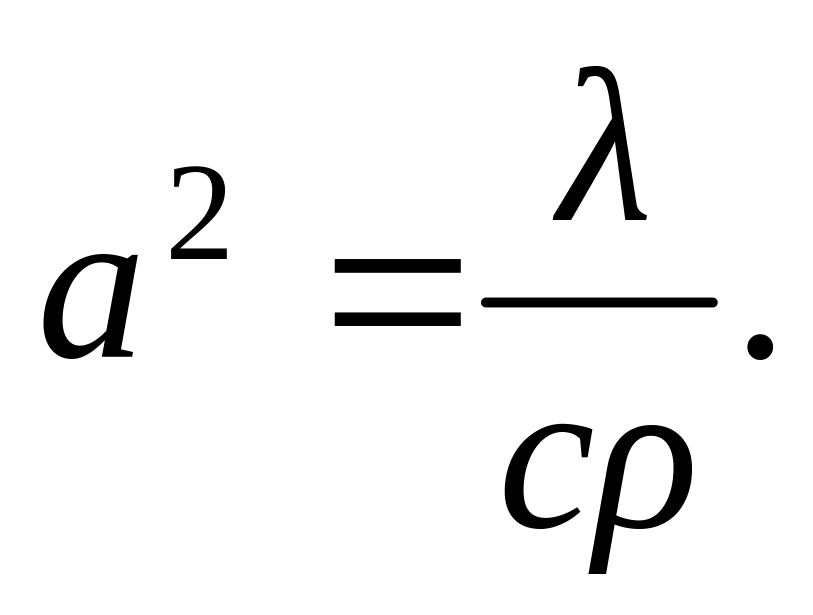
Вибрати число поділу відрізка
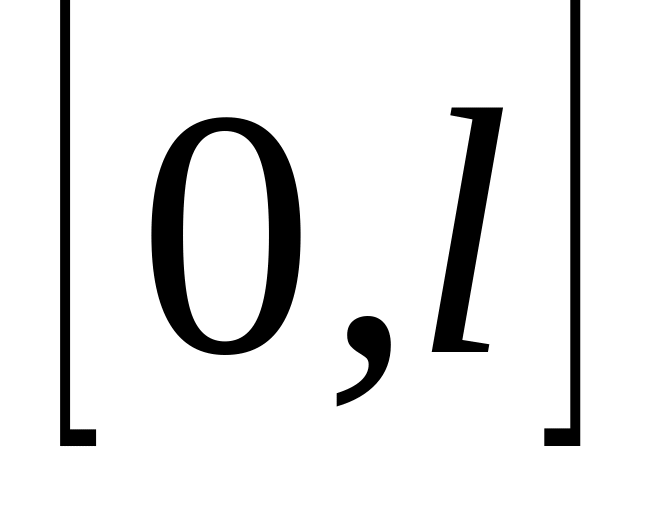 :
:
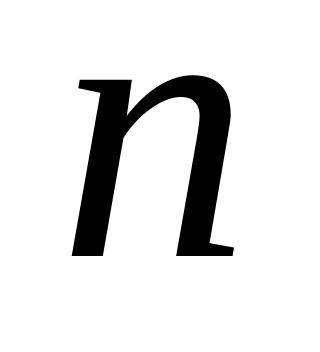 .
.Обчислити крок розбиття відрізка
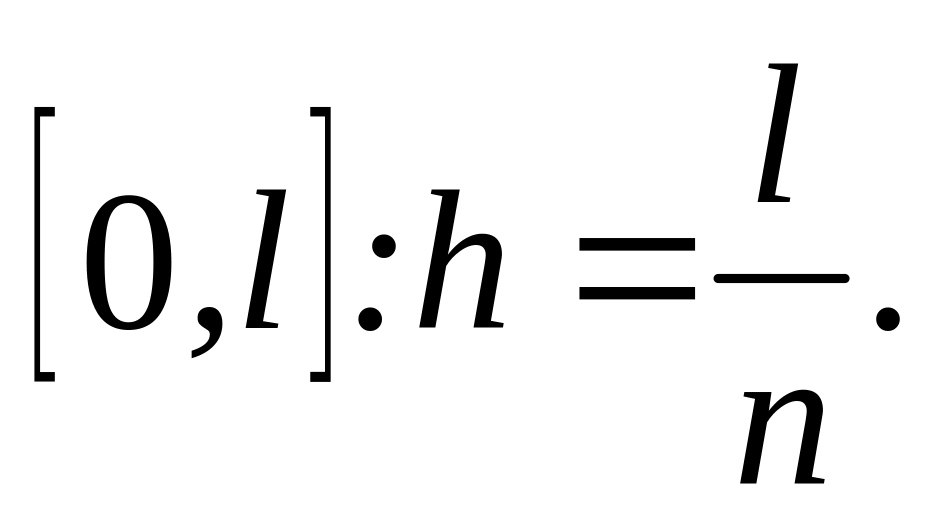
При заданому
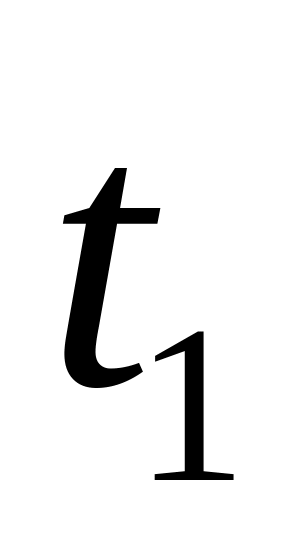 вибрати крок
по часу та розрахувати їх кількість m.
вибрати крок
по часу та розрахувати їх кількість m.Обчислити коефіцієнт
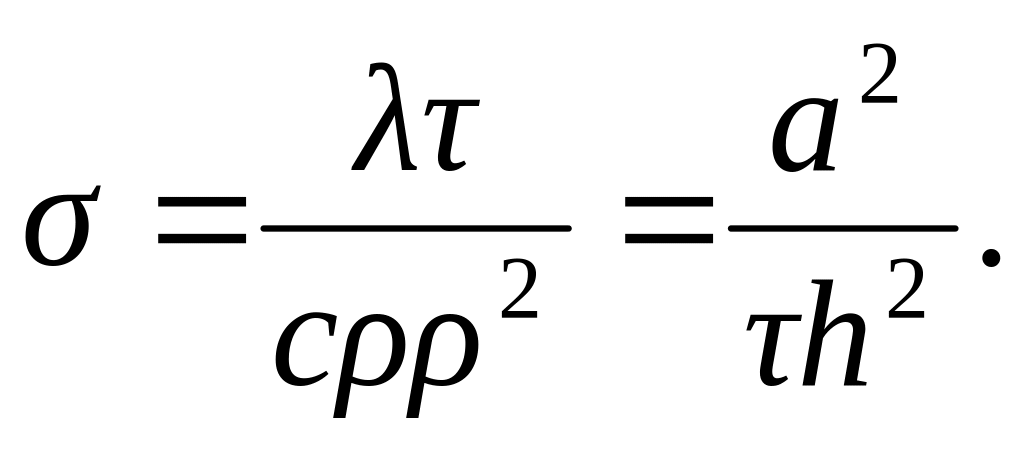
Покрити область
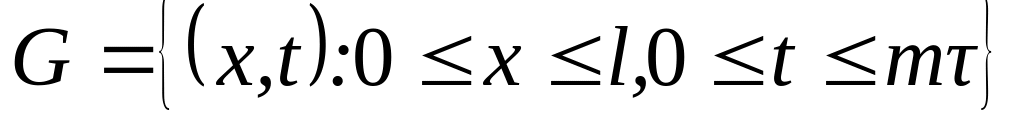 різницевою сіткою з кроками h
і
.
різницевою сіткою з кроками h
і
.Користуючись початковою умовою, обчислити
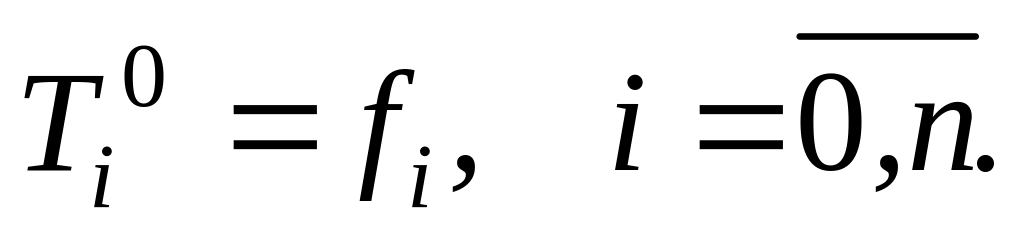
Користуючись граничними умовами, обчислити
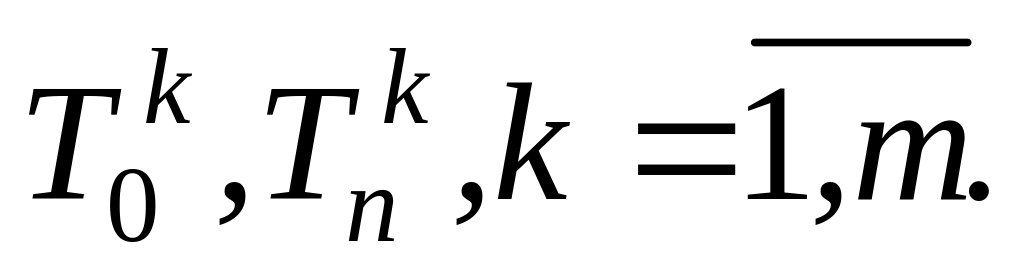
Записати неявну різницеву схему задачі,
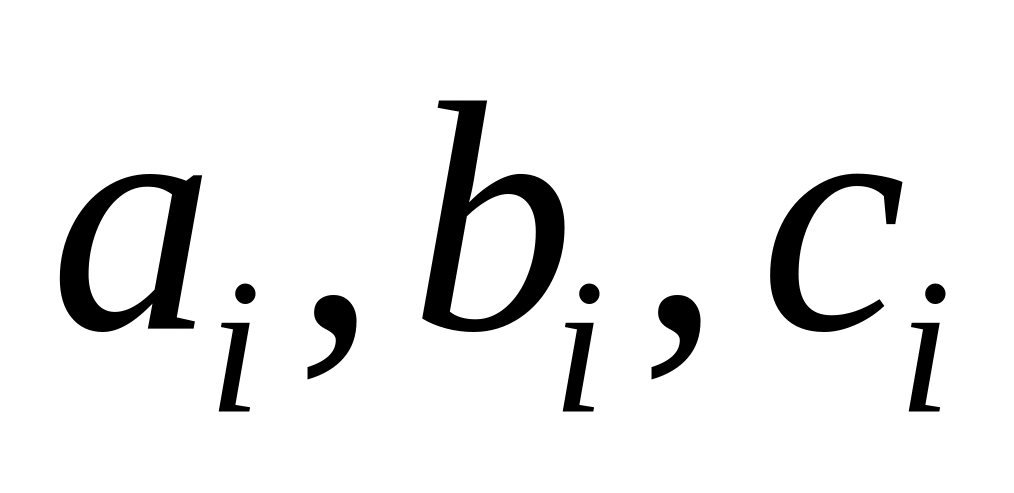 для кожного часового шару
для кожного часового шару
а) в результаті прямого ходу, обчислити прогоночні коефіцієнти
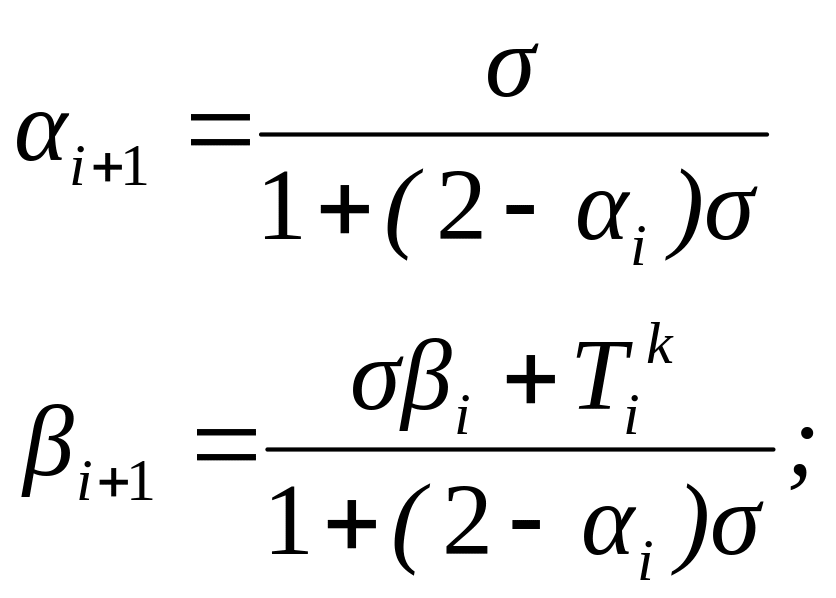
![]()
![]()
б) в
результаті зворотного ходу обчислити
значення температури
![]()
8. Різні сімейства різницевих схем для рівняння теплопровідності
8.1 Деякі позначення
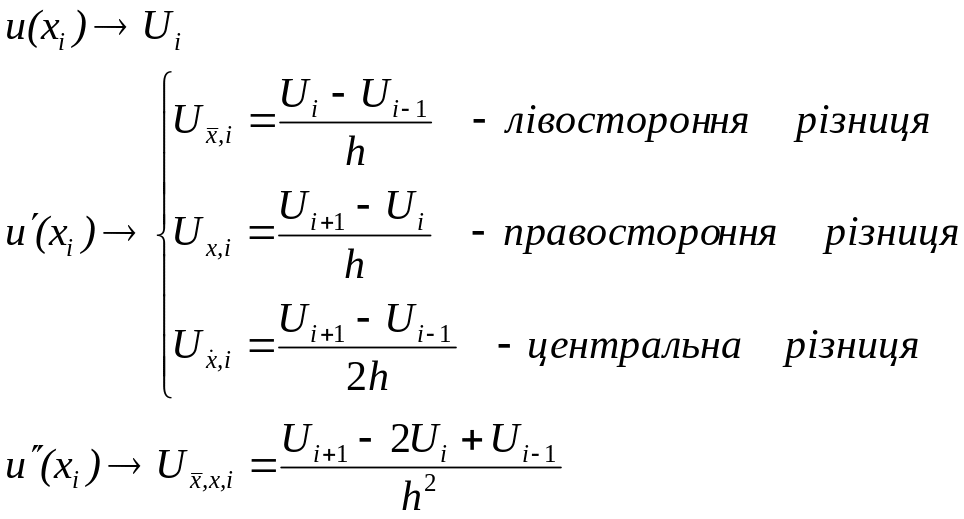
8.2 Різні сімейства різницевих схем для рівняння теплопровідності
На даний час ми розглянули дві різницевих схеми: явну і неявну. Розглянемо інші різницеві схеми для рівняння теплопровідності
![]() (8.1)
(8.1)
Розглянемо шеститочковий шаблон (рис. 8.1)
i-1,k+1
i,k+1 i+1,k+1
i-1,k
i,k
i+1,k

Рис. 8.1.
8.2.1 Різнецева схема Кранка-Ніколсона
Шеститочковою симетричною різницевою схемою для рівняння теплопровідності (8.5) називається різницева схема
![]() (8.2)
(8.2)
Дану різницеву схему отримаємо з таких міркувань:
![]()
В розгорнотому вигляді дана різницева схема представляється:
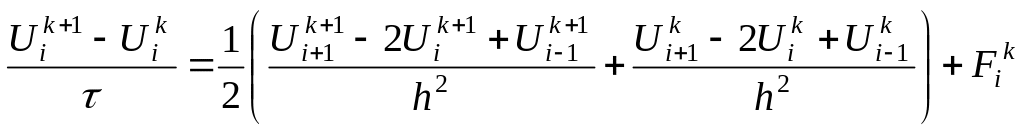 (8.3)
(8.3)
Дану
різницеву схему на шеститочковому
шаблоні для рівняння теплопровідності
називають ще схемою
Кранка-Ніколсона.
Значення
![]() на
шарі знаходиться методом прогонки. Дане
рівняння в прогоночному вигляді є
наступним:
на
шарі знаходиться методом прогонки. Дане
рівняння в прогоночному вигляді є
наступним:
![]() ,
(8.4)
,
(8.4)
де
коефіцієнти
![]() знаходяться із формули (8.3).
знаходяться із формули (8.3).
![]()
![]() ;
;
Розв’язок знаходиться методом прогонки
![]() ,
,
де
![]()
Для даної схеми початкові та граничні умови і їх апроксимація задається як і раніше (дивись неявну різницеву схему).
Можна
довести, що ця схема має другий порядок
апроксимації, як по
![]() так і по
,
якщо тільки
так і по
,
якщо тільки
![]() .
Вона абсолютно
стійка
і її розв’язок можна отримати методом
прогонки.
.
Вона абсолютно
стійка
і її розв’язок можна отримати методом
прогонки.
8.2.2 Різнецева схема з вагами
Узагальнення
трьох розглянутих різницевих схем є
однопараметрична
сім’я
різницевих схем з вагами. З цією метою
задамо довільний дійсний параметр
![]() і визначимо різницеву схему для рівняння
(8.1).
і визначимо різницеву схему для рівняння
(8.1).
![]() (8.5)
(8.5)
В
залежності від значення
![]() ,
отримаємо такі випадки:
,
отримаємо такі випадки:
При
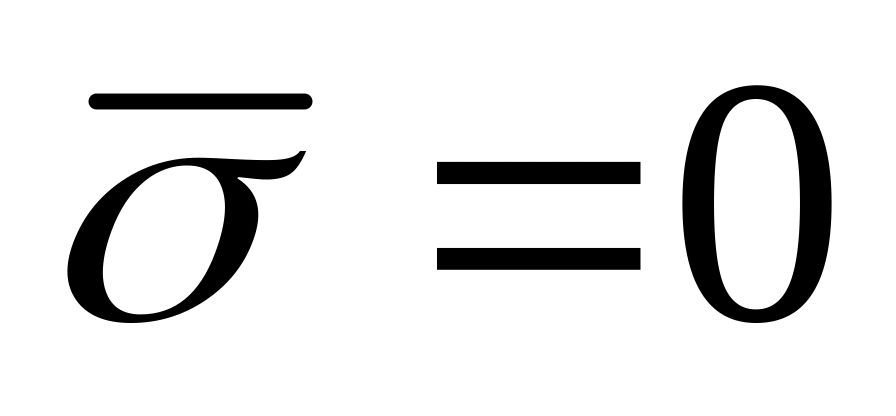 для
(8.5)
маємо явну різницеву схему, порядок
апроксимації якої
для
(8.5)
маємо явну різницеву схему, порядок
апроксимації якої
 ;
;При
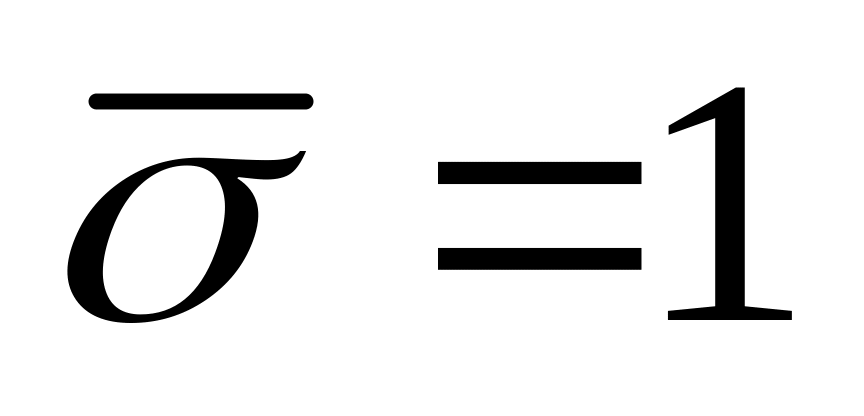 для
(8.5)
маємо чисто
неявну різницеву схему, порядок
апроксимації якої
;
для
(8.5)
маємо чисто
неявну різницеву схему, порядок
апроксимації якої
;При
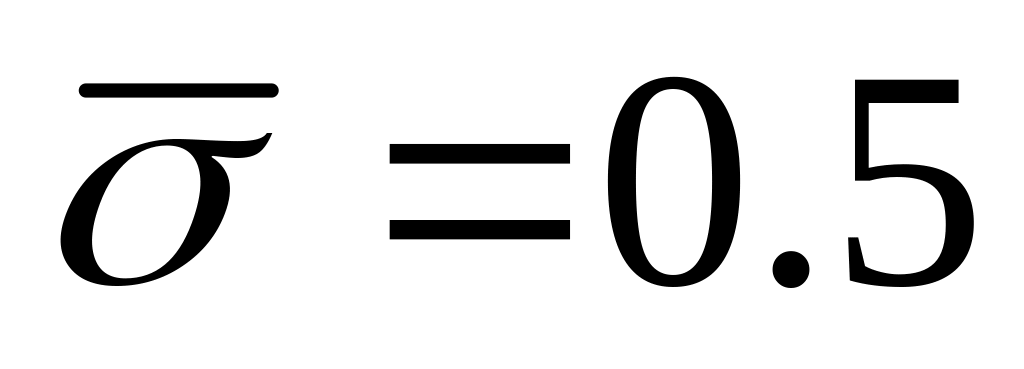 для
(8.5)
маємо шеститочкову симетричну різницеву
схему, порядок апроксимації якої
для
(8.5)
маємо шеститочкову симетричну різницеву
схему, порядок апроксимації якої
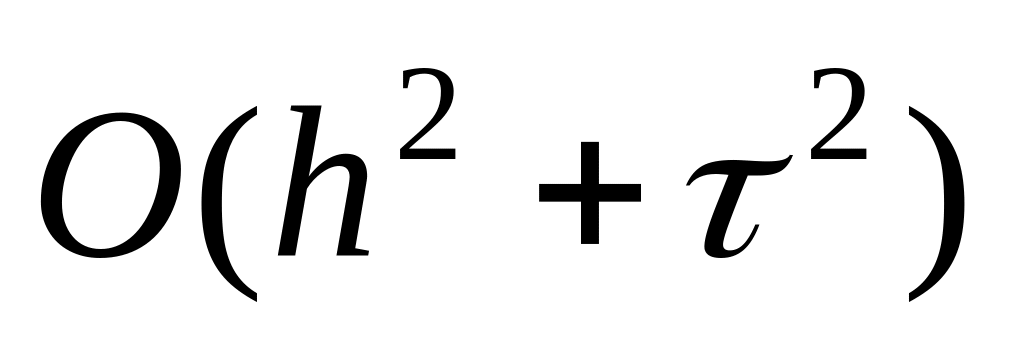 ;
;При
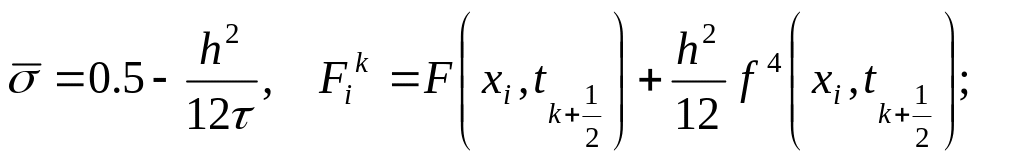
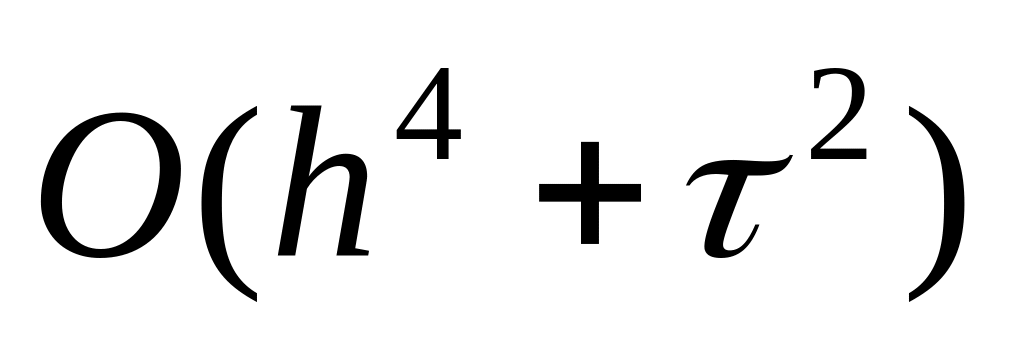 ;
;
де
![]() -
задає початкову умову.
-
задає початкову умову.
Для інших
 порядок апроксимації рівний
.
порядок апроксимації рівний
.
8.3 Різницеві схеми для рівняння теплопровідності із змінними коефіцієнтами
До цього часу ми розглядали різницеві схеми для рівняння теплопровідності з сталими коефіцієнтами (коли матеріал стержня був однорідний).
Однак, на практиці зустрічаються задачі, коли матеріал стержнів є неоднорідний. В цьому випадку він володіє різними теплофізичними властивостями в кожній точці і в кожний момент часу.
Розглянемо постановку 1-ї крайової задачі для одновимірного рівняння теплопровідності типу із змінними коефіцієнтами:
![]() ,
(8.6)
,
(8.6)
![]() ,
(8.7)
,
(8.7)
![]() ,
(8.8)
,
(8.8)
![]() ,
(8.9)
,
(8.9)
де![]() -
густина стержня;
-
густина стержня;
![]() -
коефіцієнт теплопровідності.
-
коефіцієнт теплопровідності.
Нехай
![]() - досить гладкі функції, тобто мають
похідні потрібних порядків по всіх
змінних.
- досить гладкі функції, тобто мають
похідні потрібних порядків по всіх
змінних.
Для
отримання різницевої схеми задачі
(8.6)-(8.9), апроксимуємо
![]() .
Його різницевим аналогом є
.
Його різницевим аналогом є
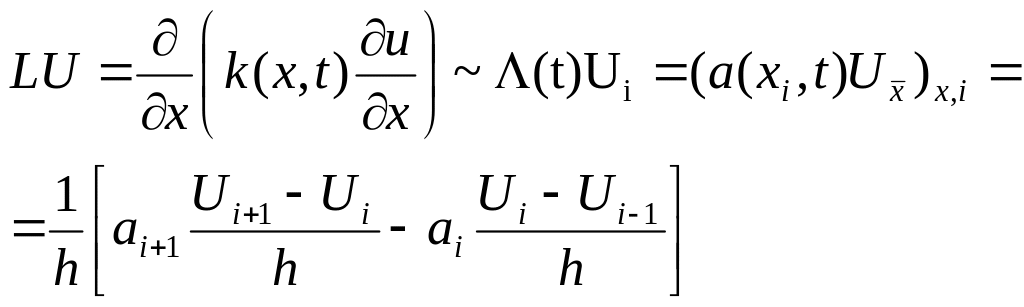 (*)
(*)
![]() -
різницевий коефіцієнт теплопровідності,
який задається умовами другого порядку
апроксимації, а саме:
-
різницевий коефіцієнт теплопровідності,
який задається умовами другого порядку
апроксимації, а саме:
 (8.10)
(8.10)
Для знаходження використаємо одне із співвідношень:
![]() ,
(8.11)
,
(8.11)
![]() ,
(8.12)
,
(8.12)
![]() (8.13)
(8.13)
Тоді для задачі (8.11)-(8.14) різницева схема з вагами матиме вигляд
![]()
Різницевий
оператор
![]() має
вигляд (*).
має
вигляд (*).
Висновки:
При маємо явну різницеву схему, тобто
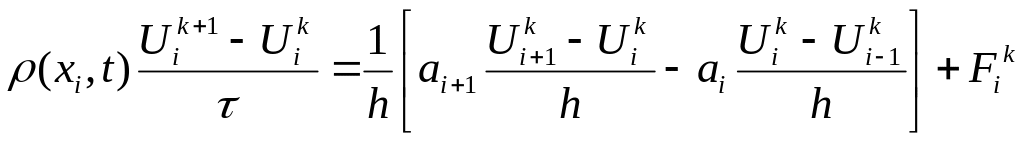 ,
яка легко розв’язується.
,
яка легко розв’язується.При
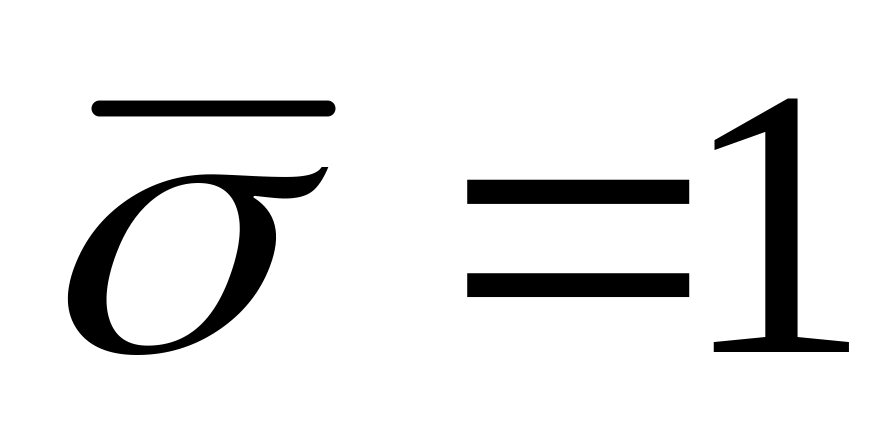 маємо
неявну різницеву схему, тобто
маємо
неявну різницеву схему, тобто
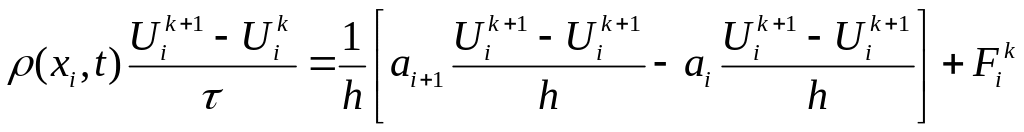 ,
яка має порядок апроксимації
,
яка має порядок апроксимації
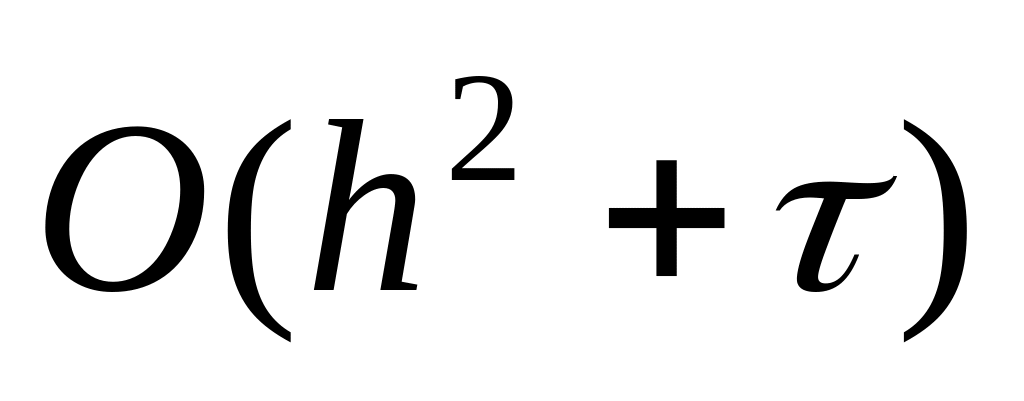 .
.При
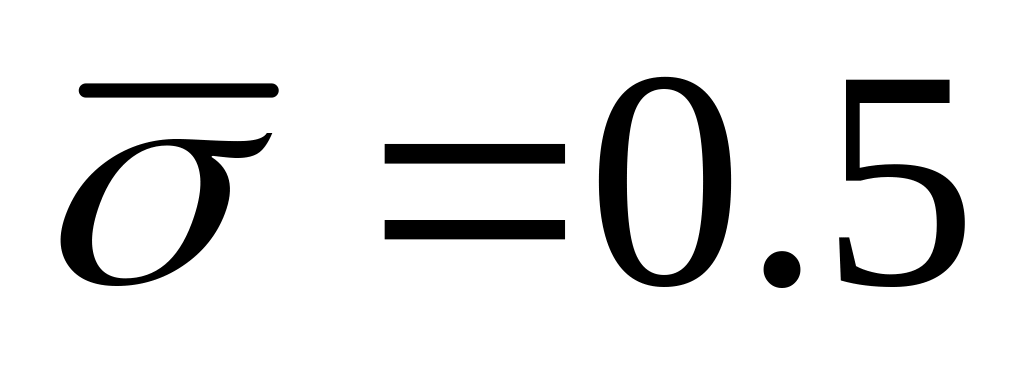 і
і
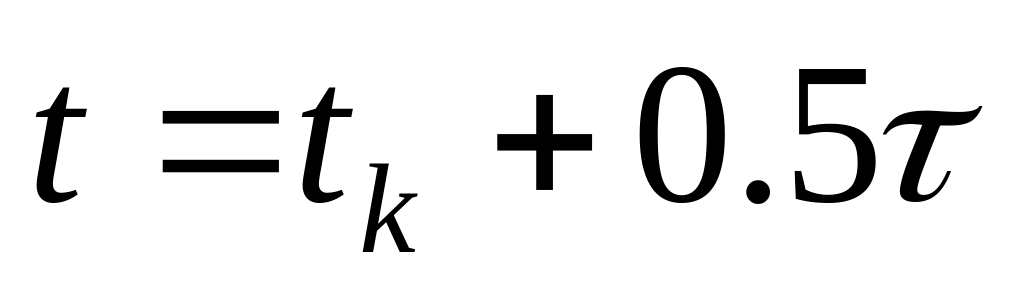 отримаємо шеститочкову різницеву
схему, яка має порядок апроксимації
.
отримаємо шеститочкову різницеву
схему, яка має порядок апроксимації
.Для всіх інших отримаємо різницеву схему з вагами, яка має порядок апроксимації .
Для дослідження стійкості різницевої схеми із змінними коефіцієнтами застосовується так званий принцип “заморожених коефіцієнтів”.
В другому, третьому та четвертому випадку для (8.14) –(8.16) різницева схема отримується неявною і її розв’язок знаходиться методом прогонки. Для застосування методу прогонки, рівняння (8.14) потрібно представити в прогоночному вигляді. Для простоти отримаємо ці коефіцієнти при . Тоді рівняння (8.14) запишеться так
![]() (8.17)
(8.17)
![]() (8.18)
(8.18)
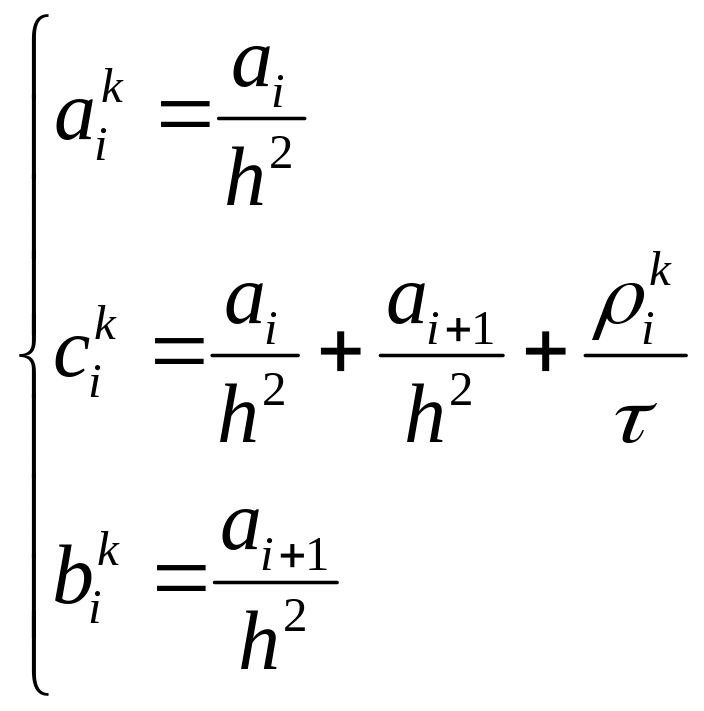 (8.19)
(8.19)
![]() (8.20)
(8.20)
де
![]() ,
,
![]()
Інші коефіцієнти аналогічні попереднім (дивись неявну різницеву схему).
