15.4.1. Постановка задачі.

Нехай маємо деяку крайову задачу

АφL, (15.1)

L – лінійний диференціальний оператор, наприклад, еліптичного типу.

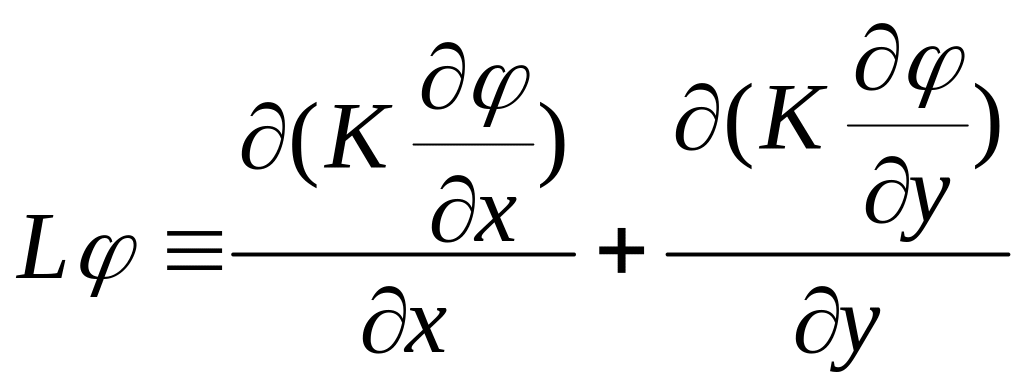
 не залежить від 

Крім того задана крайова умова:

В  M + r =0 на Г (15.2)

де М – відповідний лінійний оператор

r не залежить від 

Зокрема М може задавати граничну умову першого роду, другого роду і т. д. наприклад,

а) М=, (15.3)

б) М=k(/n).

Таким чином ставиться крайова задача для рівняння еліптичного типу.

15.4.2. Апроксимація базисними функціями.

Припустимо, що потрібно апроксимувати задану функцію  в деякій області  обмеженій замкнутою кривою  .

В задачах, що описуються диференціальними рівнянням (15.1) необхідно знайти розв’язок, що задовільняє певним крайовим умовам. Тому побудуємо спочатку апроксимацію, яка на межі  приймала б ті ж самі значення, що й функція .

Якщо знайти деяку функцію , яка приймає на однакові значення з , тобто , і ввести систему лінійно - незалежних базисних функцій , таких, що

, m, (15.4)

то можна запропонувати таку апроксимацію для  на області :

, (15.5)

д е коефіцієнти – деякі невідомі константи (параметри), які обчислюються таким чином, щоб отримати хороше наближення. Базисні функції цього типу називаються функціями форми, або пробними функціями.

Спосіб визначення функції  і системи базисних функцій автоматично забезпечує той факт, що апроксимація (15.5) володіє властивістю

(15.6)

Очевидно, що система базисних функцій повинна бути вибрана таким чином, щоб гарантувати покращення апроксимації при зростанні числа М використовуваних базисних функцій. Умова подібної збіжності апроксимації така: система базисних функцій повинна володіти тією властивістю, що комбінація

при М∞ може як завгодно точно представляти функцію φ, що задовольняє умову . Це так звана умова повноти.

Зауваження!

При великому числі базисних функцій із вибраної системи обчислювальна похибка може катастрофічно нівелювати наближений розв’язок.

15.4.3. Вибір параметрів .

В методі зважених нев’язок параметри вибираються на основі вимоги, що апроксимація повинна співпадати з функцією φ в m різних довільно вибраних точках області Ω. Ця вимога приводить до системи лінійних рівнянь відносно набору параметрів { , m=1,2,…,M}

Приклад.

Всяку неперервну функцію φ(х) на відрізку [0,1] можна апроксимувати, вибравши одну із систем базисних функцій

а) { },

б) { }.

В даному випадку функція ψ повинна бути вибрана просто як лінійна функція, що приймає ті ж значення, що й φ при і . А параметри вибираємо таким чином, щоб

при ,

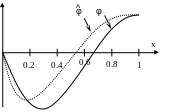
1 5.4.4 Апроксимація за допомогою зважених нев’язок.

Нехай необхідно апроксимувати . Для цього потрібно визначити .

Розглянемо більш загальний метод визначення сталих в апроксимації (15.5). В зв’язку з цим, введемо похибку або нев’язку апроксимації:

(15.7)

Зауважимо, що – це функція, яка залежить від координат точки із області . Щоб зменшити цю нев’язку деяким чином на всій області , будемо вимагати рівність нулю відповідного числа інтегралів від похибки, взятих із різними вагами

, (15.8)

де {W , ℓ=1,2, ...} – множина лінійно-незалежних вагових функцій, які іноді називають пробними функціями. Тоді загальну вимогу збіжності можна записати у формі виконання умови (15.8) ℓ, при М. А це буде тоді, коли R 0 у всіх точках області . Підставивши (15.5) у (15.8), отримаємо систему рівнянь методу зважених нев’язок (15.8) у формі СЛАР для невідомих коефіцієнтів :

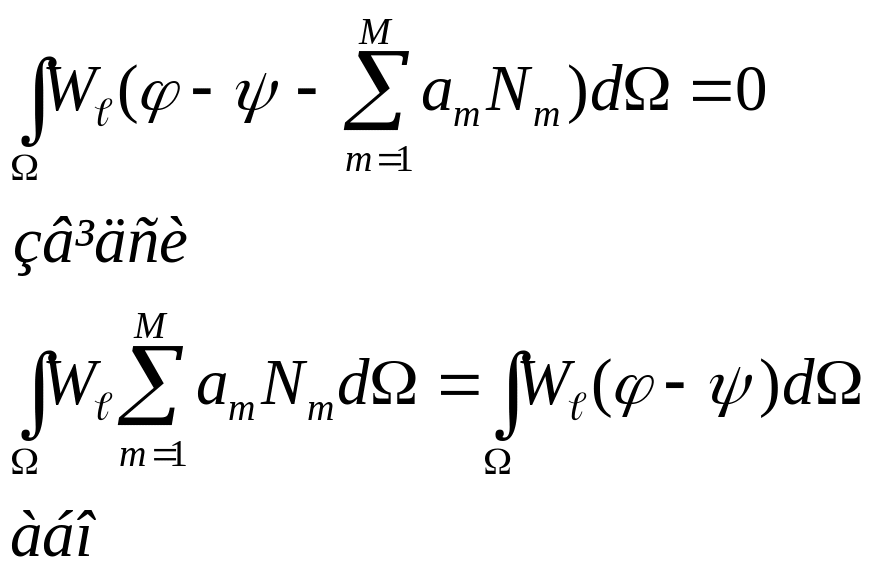
(15.9)

Ввівши позначення , (15.10)

(15.11)

Отримаємо систему лінійно-незалежних алгебраїчних рівнянь: (15.12)

В матричній формі

(15.13)

В розгорнутій формі:

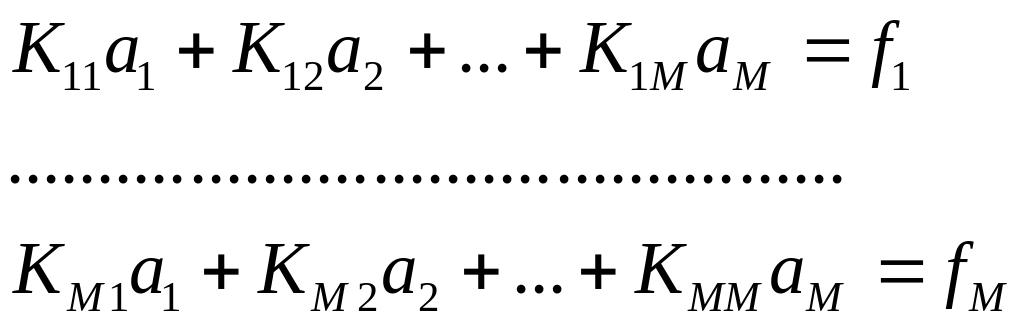(15.14)

Таким чином, ми отримали систему рівнянь методу зважених нев’язок у формі СЛАР для невідомих коефіцієнтів .

Отже, якщо відома апроксимуюча функція , визначена функція , така що виконується умова (15.4) і вибрані підходящі системи базисних функцій і вагових функцій , то розв’язуючи (15.12) можна отримати коефіцієнти в апроксимації (15.5). На практиці можуть бути використані різні види систем вагових функцій , що ведуть до різних методів апроксимації методом зважених нев’язок. Вони вибираються на основі методів:

1. методу початкової колокації

2. колокації по під областях

3. методу Гальоркіна

Розглянемо метод Гальоркіна. В цьому найбільш популярному методі зважених нев’язок замість вибору нової системи функції в якості вагових множників вибираються самі базисні функції, тобто (13) . Тоді в системі рівнянь (10) елементи матриці К і вектор f мають вигляд:

(14)

(15)

Варто зауважити, що симетричність матриці k забезпечує методу обчислювальні переваги. Цей метод вперш був використаний Гальоркіним і носить його ім’я

Іноді (зважену) загальну схему методу зважених нев’язок, а цей метод називається методом Бубнова-Гальоркіна.

5.Апроксимація розв’язків краєвих задач.

Повернемось до задачі (1)-(2). Слідуючи описаній методиці, будемо будувати апроксимацію для розв’язку  у вигляді (6). Функцію  і базисні функції N_m виберемо таким чином, щоб

М=-r (16),

MN_m=0 (17) , m=1,2,… на Г тому автоматично задовільняє крайовим умовам (2), при довільних коефіцієнтах. Отримаємо апроксимації похідних з (6). Якщо функції N_m- неперервні в розглядуваній області  і всі їх похідні існують, то з (6) маємо:

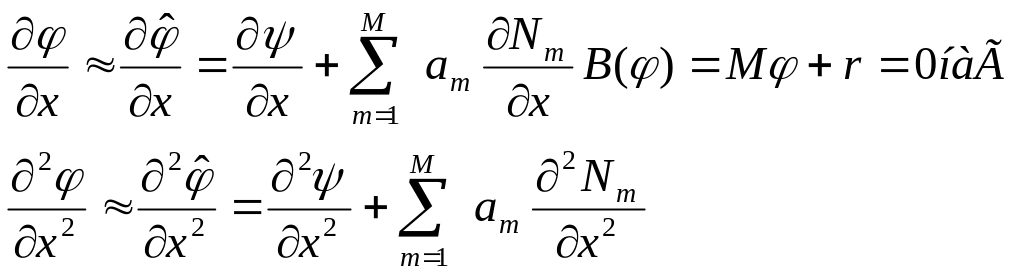
Припустимо спочатку, що всі базисні функції Nm – неперервно –диференціальні. Так, як побудований розклад (6) задов. крайовим умовам (2), то для отримання апроксимації шуканої функції , необхідно лише гарантувати, що - наближений розв’язок диференціального рівняння (1). Підставивши в диференціальне рівняння (1), отримаємо нев’язку R, яку в силу лінійності оператора L можна записати у вигляді:

(20)

L - еліптичний оператор.

Для отримання наближеної рівності =0 в  можна безпосередньо застосувати процедуру, розглянуту вище. Це дозволить знайти апроксимацію шуканої функції і. З цією метою, як і раніше, використаємо метод зважених нев’язок. Для цього виберемо деяку систему вагових функцій Wℓ і вимагаючи щоб:

(21)

Так, як загальне число невідомих =М, то застосовуючи рівняння (21), при ℓ=1,2,...М, отримаємо СЛАР, яку можна записати у вигляді (10): Ка=f (22), де коефіцієнти

(23)

Обчислюючи елем. матриці К і правої частини рівнянь, і розв’язуючи потім отриману систему, ми визначимо невідомі , m=1,...М і тим самим завершимо процес побудови наближеного розв’язку заданого диференціального рівняння. Варто зауважити, що за звичаєм матриця К є заповненою і не має тенденції до смужкової структури, характерної для матриць, які отримані в методі скінченних різниць. Можна розглянути різні вибори вагових функцій W , які розглядалися вище.

6.Одночасна апроксимація розв’язку диференціальних рівнянь і крайових умов.

Вище було показано, як можна наближено розв’язати диференціальне рівняння, використовуючи розклад по базових функціях (6) і, будуючи, апроксимуючи функцію , яка тотожньо задовольняється всім умовам задачі (1), (2). Цю умову ми дещо послабимо, оскільки це природнім чином обмежує вибір можливих базисних функцій N_m. Будемо вважати, що розклад аналогічний, як в (6),тільки без  не задовол. апріорно деякій крайовій умові або всім крайовим умовам задачі. Тоді до нев’язки по області на  добавляється нев’язка в крайових умовах

Постараємось зменшити зважену суму нев’язок на межі і по області, таким чином, щоб

(24)

Де вагові функції W можуть бути вибрані незалежно. Систему рівнянь, як потрібно розв’язати

(25)

Природні крайові умови:

При одночасній апроксимації розв’язку крайової задачі (1), (2) використання рівняння (24) може вимагати обчислення інтегралів, що включають похідні від  вздовж межі, що може викликати труднощі, якщо ці межі криволінійні, або мають інші ускладнюючі особливості. Обходять ці труднощі так. В рівнянні (24) перший доданок перетворюють таким чином:

(26)

В (16) перший інтеграл представляють так:

(27)

Де L1,D,E- оператори лінійні, диференціальні, більш нижчого порядку, ніж оператор L.

Результат підстановки для розглянутих вище задач виразу (27) у (24) називається слабим формулюванням методу зважених нев’язок, або слабкою формою рівняння методу зважених нев’язок.

Після такої підстановки певним вибором граничної вагової функції W можна добитись того, що останній доданок в (27) і частина другого доданку в (24) взаємознищуються і таким чином буде виключений інтеграл, що містить , або її похідні вздовж меж. Це буде можливо лише для певних крайових умов, які називаються природними. В загальному випадку, застосування такої процедури для крайових умов, що включають тільки задання значень самої функції, вигоди не дає, але може бути корисна при задані на межі похідної. Ще одна перевага такого перетворення полягає в певній симетрії відповідних алгебричних рівнянь, поряд з отриманням, взагалі кажучи, більш низького порядку похідних базисних функцій N .