
- •Оглавление
- •Введение. Цели и задачи дисциплины.
- •Указания по оформлению контрольных заданий
- •Содержание дисциплины.
- •Методические указания по изучению тем программы
- •Правила дифференцирования функций
- •Неопределённый интеграл и его свойства.
- •Определённый интеграл и его свойства.
- •Задания для самоконтроля Контрольная работа (1 курс)
- •Самостоятельная работа.
- •Контрольная работа по математике ( 2 курс)
- •Подготовка к контрольной работе по математике
- •Итоговый тест по математике
- •Задания для контрольных работ
- •Тема 1. Вычисление производной
- •Тема 2. Приложение дифференциального исчисления
- •Тема 3. Определенный интеграл и его приложения
- •Тема 1. Вычисление производной
- •Тема 2. Приложение дифференциального исчисления
- •Тема 3. Определенный интеграл и его приложения
- •Тема 1. Вычисление производной
- •Тема 2. Приложение дифференциального исчисления
- •Тема 3. Определенный интеграл и его приложения
- •Тема 1. Вычисление производной
- •Тема 2. Приложение дифференциального исчисления
- •Тема 3. Определенный интеграл и его приложения
- •Тема 1. Вычисление производной
- •Тема 2. Приложение дифференциального исчисления
- •Тема 3. Определенный интеграл и его приложения
- •Тема 1. Вычисление производной
- •Тема 2. Приложение дифференциального исчисления
- •Тема 3. Определенный интеграл и его приложения
- •Тема 1. Вычисление производной
- •Тема 2. Приложение дифференциального исчисления
- •Тема 3. Определенный интеграл и его приложения
- •Тема 1. Вычисление производной
- •Тема 2. Приложение дифференциального исчисления
- •Тема 3. Определенный интеграл и его приложения
- •Тема 1. Вычисление производной
- •Тема 2. Приложение дифференциального исчисления
- •Тема 3. Определенный интеграл и его приложения
- •Тема 1. Вычисление производной
- •Тема 2. Приложение дифференциального исчисления
- •Тема 3. Определенный интеграл и его приложения
- •Вопросы к зачёту.
- •Вопросы к экзамену.
- •Список рекомендуемой литературы.
Неопределённый интеграл и его свойства.
Если
функция F(x)
– первообразная для функции f(x),
то множество функций F(x)+C,
где С – произвольная постоянная,
называется неопределённым интегралом
от функции f(x)
и обозначается символом
![]() .
При этом функция f(x)
наз. подынтегральной функцией, f(x)dx
– подынтегральным выражением, ф
переменная x
– переменной интегрирования. Интегрирование
– операция, обратная дифференцированию.
.
При этом функция f(x)
наз. подынтегральной функцией, f(x)dx
– подынтегральным выражением, ф
переменная x
– переменной интегрирования. Интегрирование
– операция, обратная дифференцированию.
Свойства:
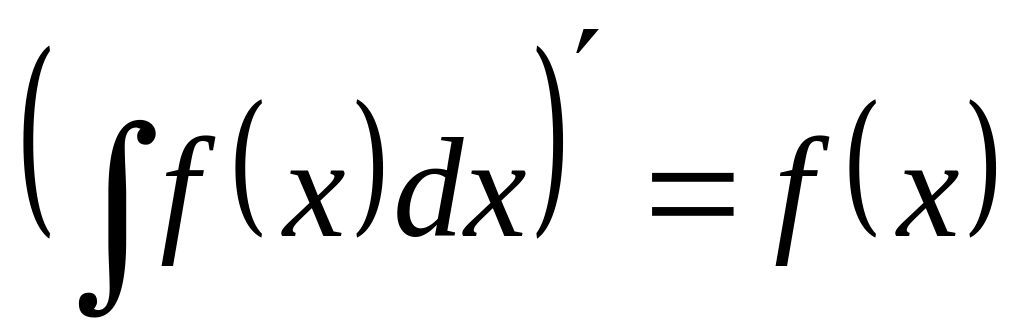
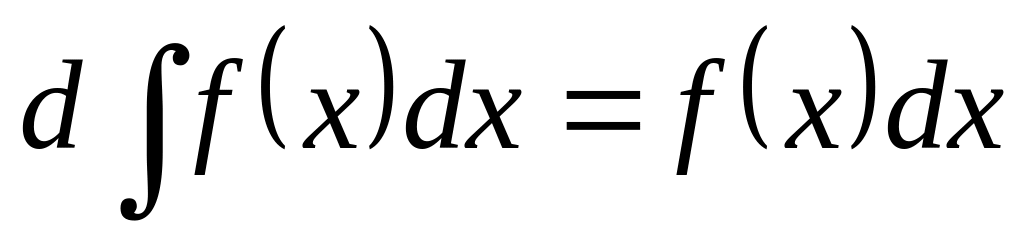
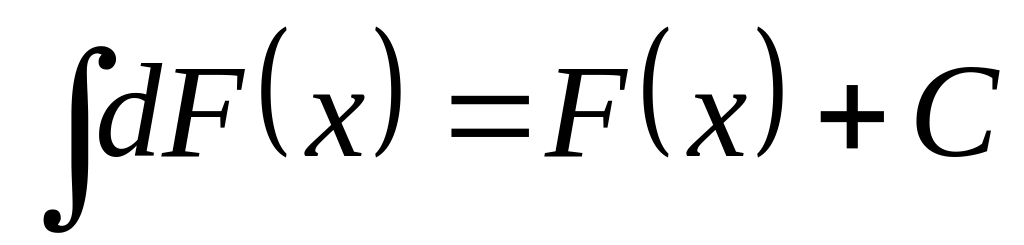
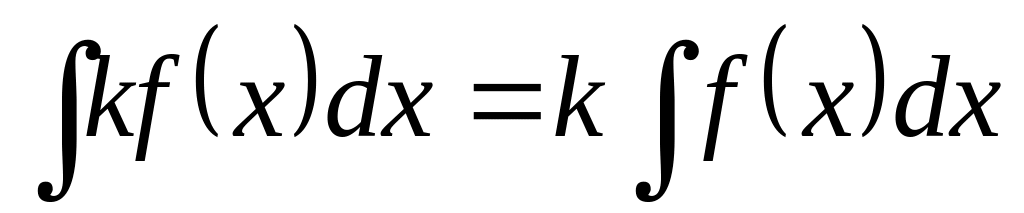
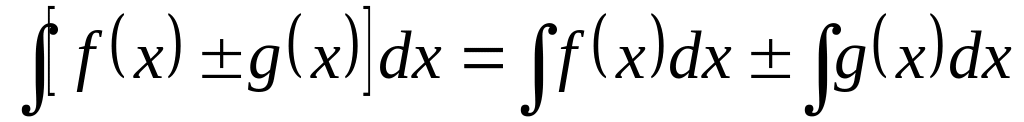 .
.
Метод подстановки (неопределённый интеграл).
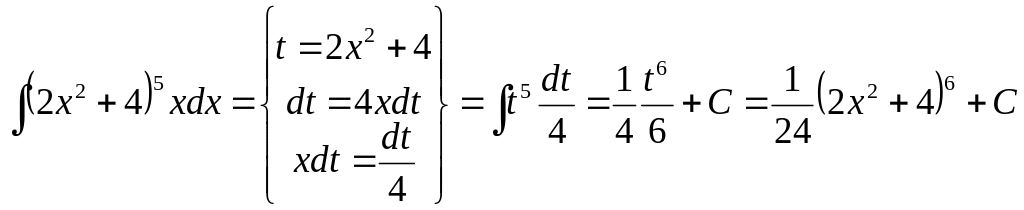
Вычисление неопределённого интеграла по частям.
![]()
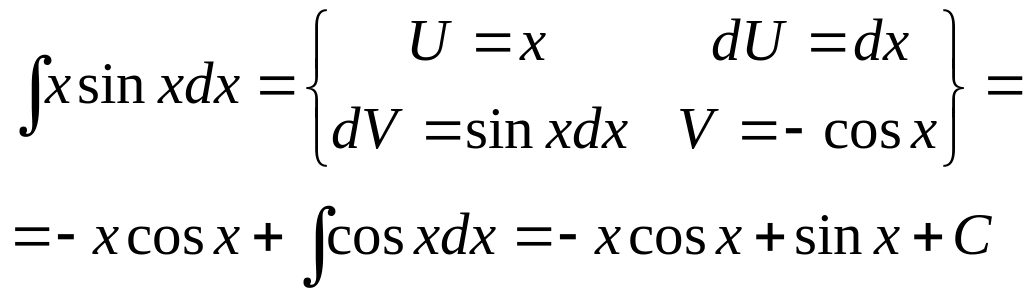
Определённый интеграл и его свойства.
Если
существует конечный предел I
интегральной суммы, то этот предел наз.
определённым интегралом от функции
f(x)
по отрезку [a,
b]
и обозначается:
![]()
Свойства:
по определению
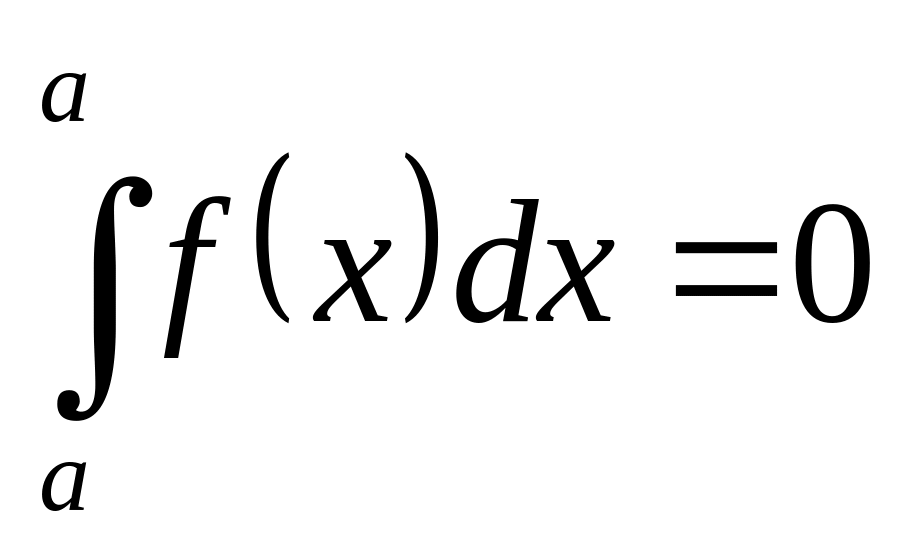
по определению
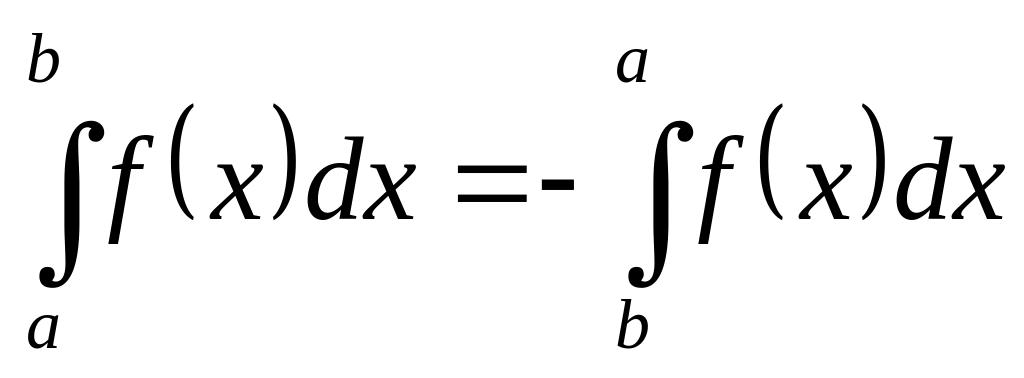
каковы бы ни были числа a, b, c, всегда имеет место равенство
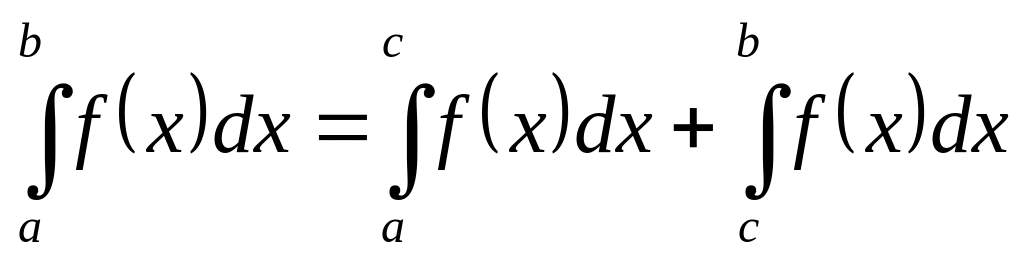
постоянный множитель можно выносить за знак определённого интеграла

определённый интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов
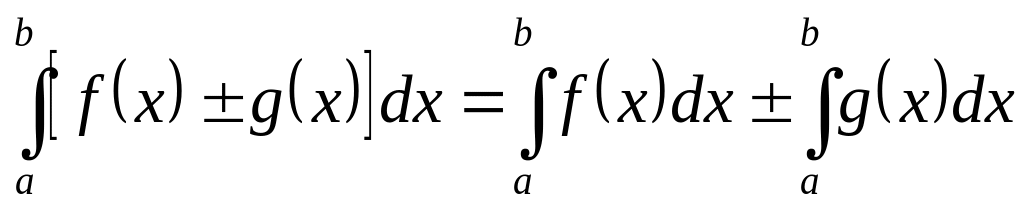
Формула Ньютона-Лейбница. Непосредственное интегрирование.
![]()
![]()
Метод подстановки (определённый интеграл).
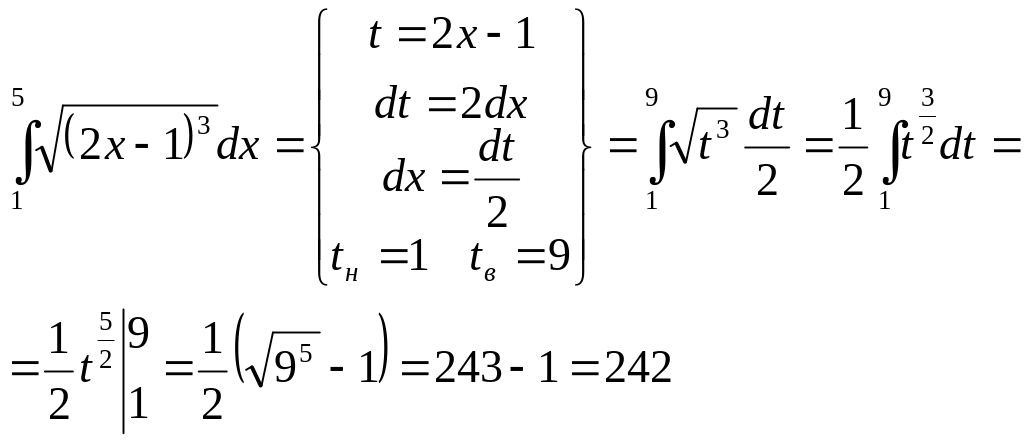
Вычисление площадей плоских фигур.
![]()
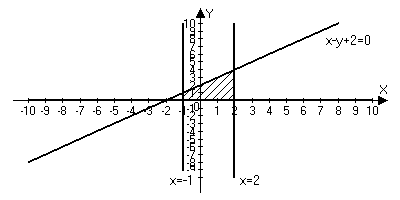
x-y+2=0
y=0
x=-1
x=2
S - ?
![]()
В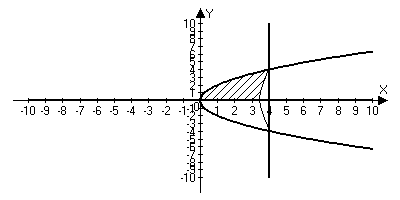 ычисление
объёмов тел вращения.
ычисление
объёмов тел вращения.
y 2=4x
2=4x
y=0
x =4
=4
Vx - ?
![]()
Вычисление пути, пройденного точкой.
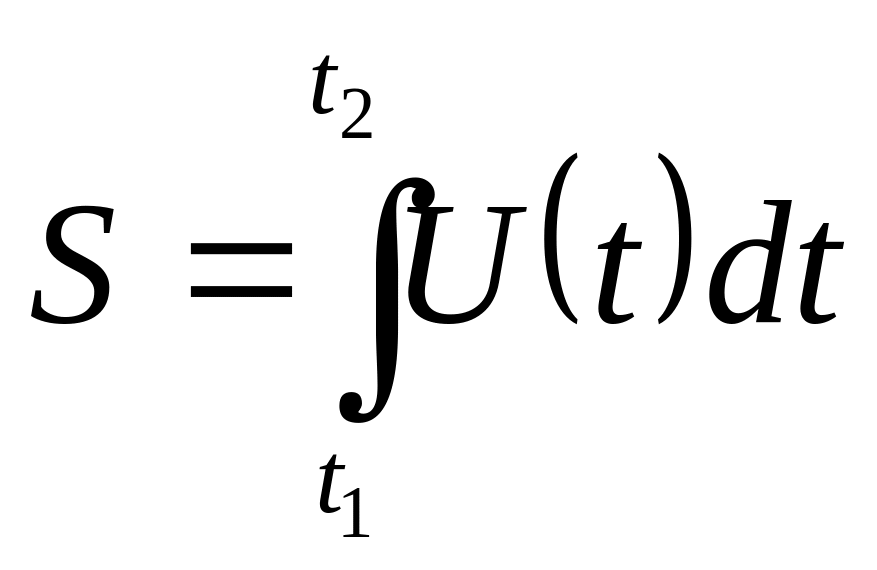
U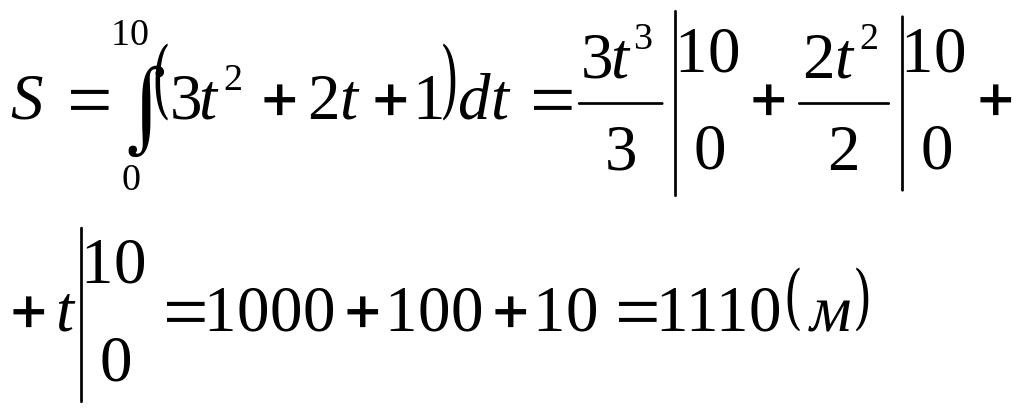 =3t2+2t+1(м/с)
=3t2+2t+1(м/с)
t1=0c
t2=10c
S - ?
Задания для самоконтроля Контрольная работа (1 курс)
Вариант 1
1. Представить в виде обыкновенной дроби: а) 0,(6) б) 1,(55) в) 0,1(2).
2.
Упростить выражения: а)
![]() б) |
б) |
![]() |
|
3. Решить уравнения: а) | x-2|=1
б) | x-2| + |1-x| =3
в)
![]() = х-1
= х-1
г)
![]()
4. Решить неравенства: а) | 2x+6 | < 6
б)
![]()
в)
![]()
5. Решить систему уравнений:
а)
![]() б)
б)
![]()
Вариант 2
1. Представить в виде обыкновенной дроби: а) 0,(11) б) 1,(5) в) 0,2(1).
2.
Упростить выражения: а)
![]() б) |√3-2|
б) |√3-2|
3. Решить уравнения: а) | x-1|=2
б) | x+2| + |1-x| =4
в)
![]()
г)
![]()
4. Решить неравенства: а) | 3x+2 | < 5
б)
![]()
в)
![]()
5. Решить систему уравнений:
а)
![]() б)
б)
![]()
Вариант 3.
1. Представить в виде обыкновенной дроби: а) 0,(8) б) 5,(1) в) 2,1(2).
2.
Упростить выражения: а)
![]() б) |√3-√2|
б) |√3-√2|
3. Решить уравнения: а) |2х+1|=5
б) | x+1| + |2-x| =4
в)
![]()
г)
![]()
4. Решить неравенства: а) | 4-х| ≥3
б)
![]() < 1
< 1![]()
в)
![]()
5. Решить систему уравнений:
а)
![]() б)
б)
![]()
Вариант 4.
1. Представить в виде обыкновенной дроби: а) 0,(7) б) 3,4(1) в) 2,(1).
2.
Упростить выражения: а)
![]() б) |√5-√7|
б) |√5-√7|
3. Решить уравнения: а) |4х-3|=8
б) | x+7| + |6-x| =1
в)
![]()
г)
![]()
4. Решить неравенства: а) | 2-х| ≥5
б)
![]() < 2
< 2
в)
![]()
5. Решить систему уравнений:
а)
![]() б)
б)
![]()
