Федеральное агентство железнодорожного транспорта

Омский государственный университет путей сообщения

Кафедра «Системы передачи информации»

СЛУЧАЙНЫЕ СИГНАЛЫ И ФУНКЦИЯ КОРРЕЛЯЦИИ

Лабораторная работа № 3

Студенты гр. 20Г

______ К. И. Корниенко

______ А. В. Ведерников

______ К. А. Ерофеева

Руководитель–

______ К. А. Бондаренко

_________

Оценка

Омск 2012

Цель работы – изучение характеристик случайных сигналов, ознакомление с методикой экспериментального исследования этих сигналов.

1. Краткие теоретические сведения

Переменная величина, которая может принимать те или иные числовые значения в зависимости от различных случайных обстоятельств, называется случайной величиной.

1.1 Прерывные случайные величины

Случайная величина называется прерывной (дискретной), если она может принимать только конечное или счетное число значений. Данные о всех возможных значениях случайной величины еще недостаточны для ее полной характеристики. Нужно знать для каждого значения вероятность, с которой случайная величина принимает именно это значение 1, с. 23  42; 2, с. 38  49; 3, с. 49  79; 4, с. 142  190:

P(x = x_i) = P_i (i = 1, 2, 3, …, n). (1.1)

Функция Р(х), связывающая значения случайной величины с соответствующими им вероятностями, представляет собой закон распределения дискретной случайной величины. Составить представление о случайной величине только по Р(х) часто бывает весьма трудно, поэтому возникает необходимость дать характеристику случайной величины с помощью постоянных чисел. Они должны получаться на основе значений случайной величины и соответствующих им вероятностей и характеризовать случайную величину в целом, отражать закономерности, присущие ей. Такими величинами являются моменты разных порядков. Математическим ожиданием прерывной случайной величины называется сумма произведений всех ее возможных значений на соответствующие им вероятности. Математическое ожидание случайной величины х обозначаются символом Мх,

. (1.2)

Математическое ожидание случайной величины называют ее средним значением. Оно характеризует ее «в среднем», показывает, какое значение случайной величины следует ожидать «в среднем» при испытаниях или наблюдениях. По математическому ожиданию нельзя судить о том, какие отклонения от него, хотя бы в среднем, имеют место как в меньшую, так и в большую сторону, т. е. какова степень рассеяния случайной величины. Наиболее распространенной мерой рассеяния является так называемая дисперсия и непосредственно получаемое из нее среднеквадратичное отклонение.

Дисперсией D_х случайной величины называется математическое ожидание квадрата отклонения ее от своего математического ожидания:

, (1.3)

где m = Мх  математическое ожидание.

Арифметическое значение корня квадратного из дисперсии называется среднеквадратичным отклонением случайной величины:

. (1.4)

Среднеквадратичное отклонение характеризует степень отклонения случайной величины от ее математического ожидания и имеет размерность случайной величины.

1.2 Непрерывные случайные величины

Случайная величина называется непрерывной, если функция распределения ее всюду непрерывна, а производная функции распределения непрерывна во всех точках или имеет конечное число разрывов.

Плотностью вероятности, или дифференциальным законом распределе-

ния непрерывной случайной величины, называется производная ее функции распределения:

W(х) = F(х). (1.5)

Наиболее важным дифференциальным законом распределения непрерывных случайных величин является нормальный закон (закон Гаусса). Плотность вероятности случайной величины, распределенной по нормальному закону, определяется равенством:

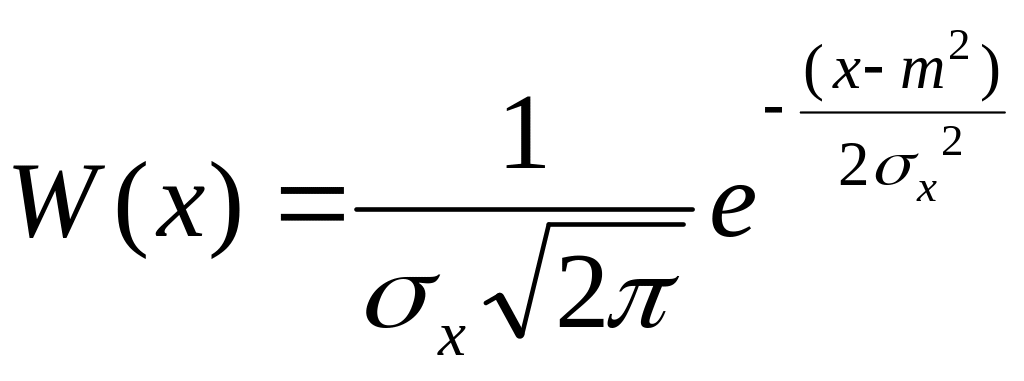, (1.6)

где m и _х  постоянные числа.

Плотность вероятности случайной величины обладает следующими свойствами:

1) она дает возможность вычислить вероятность того, что случайная величина примет какое-нибудь значение из интервала (х, х). Вероятность того, что случайная величина примет какое-нибудь значение из интервала (х, х), авна определенному интегралу от плотности вероятности:

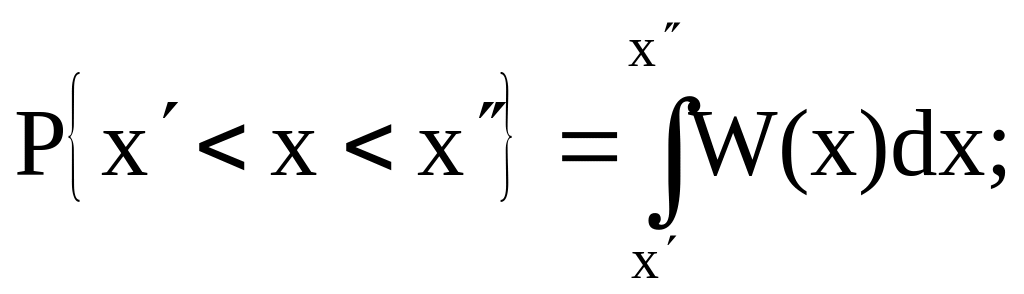(1.7)

2) плотность вероятности не отрицательна. Действительно, плотность вероятности W(х) является производной функции распределения F(x), которая не убывает ни при каких х, следовательно, W(х) не может быть отрицательной;

3) интеграл от плотности вероятности, взятый в бесконечных пределах, равен единице:

. (1.8)

По существу это свойство является следствием того, что значение случайной величины достоверно заключено в пределах от  до +. Это условие является условием нормировки плотности вероятности. Плотность вероятности W(х) имеет размерность, обратную размерности х.

График плотности вероятности непрерывной случайной величины называется кривой ее распределения.

Математическим ожиданием непрерывной случайной величины х, плотностью вероятности которой является функция W(х), будем называть величину несобственного интеграла:

, (1.9)

если он сходится абсолютно.