Нормирование случайный процессов в узкополосных линейных цепях

Пусть на входе линейной цепи действует стационарный случайный процесс с распределением отличным от нормального. Если интервал корреляции этого процесса меньше постоянной времени линейной цепи (т. е. ширина энергетического спектра больше полосы пропускания цепи), то распределение случайного процесса на выходе приближается к нормальному. Эффект нормализации тем выше, чем меньше полоса пропускания цепи.

Например. На высокодобротный контур подается случайный процесс представляющий собой последовательность импульсов со случайным и ненормальным временем появления. На выходе получаем сигнал как сумму свободных колебаний, вызванных предыдущими импульсами и не успевших затухнуть к рассматриваемому моменту времени. Чем уже полоса пропускания цепи, тем большее число соизмеримых по величине и некоррелированных слагаемы принимает участие в образовании результирующего колебания в момент времени t₁. В соответствии с центральной предельной теоремой этого вполне достаточно для того, чтобы процесс приближался к нормальному.

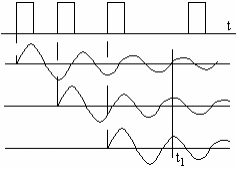
В широкополосных линейных цепях при некоторых условиях происходит обратный процесс денормализация т. е. нормальный процесс на входе порождает случайный процесс на выходе отличный от нормального.

Но такое отличие только в частности, в целом же если рассматривать бесконечное число импульсов, то процесс остается нормальным.

Комплексный случайный процесс

Пусть есть случайный процесс x(t). Подберем ему сопряженный по Гильберту сигнал x₁(t) ( .

Тогда комплексный случайный процесс: .

П усть , тогда . Отсюда комплексный случайный процесс: .

Спектры сигналов x(t) и x₁(t) равны: . Отсюда следует, что корреляционные функции одинаковы .

Дисперсии: .

Предположим, что соответствует , тогда , где . Т. е.

Отсюда следует, что при w>0 , а при w<0 .

Вывод: спектр случайного сигнала отличен от 0 только на положительных частотах.

Преобразование нормального процесса в безынерционных нелинейных цепях

В нелинейных безынерционных элементах основная трудность состоит в нахождении корреляционной функции. Поэтому общих методов анализа преобразования случайный процессов в нелинейных устройствах не существует. Приходится ограничиваться частными задачами поддающимися решению.

Пусть на нелинейный элемент действует случайное колебание с заданной плотностью вероятности p(x). Требуется найти плотность вероятности выходной величины y p(y). Связь между x и y определяется нелинейной зависимостью y=f(x). Для безынерционного элемента очевидно соотношение: , откуда вытекает .

Если обратная функция х=j(у) неоднозначна, то

Нахождение р(у) проще пояснить на конкретных примерах.

Воздействие гаусовского процесса на элемент с

симметричной квадратичной характеристикой

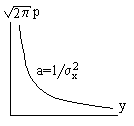
Полагая у=ах², dy/dx=2ах и учитывая, что каждому значению у соответствует 2 значения х ( ) найдем

Подставляя данные в выражение получим:

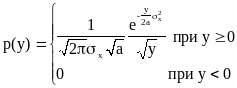
Воздействие нормально распределенного процесса на

однополупериодный детектор с линейно ломаной характеристикой

В данном случае

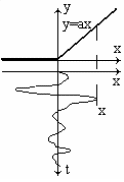
Плотность распределения вероятности в этом случае:

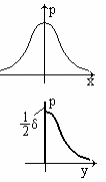
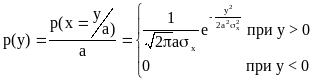
Плотность вероятности р(у=0)=¥, так как у=0 при х меньше 0. Это можно учесть записав следующее выражение для р(у):

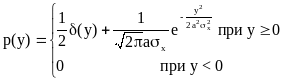
Первое слагаемое будет всюду равно 0, кроме точки у=0, где оно обращается в бесконечность. При интегрировании же по у это слагаемое дает 1/2.

Воздействие нормально распределенного

процесса на ограничитель

По аналогии с предыдущим случаем составим выражение:

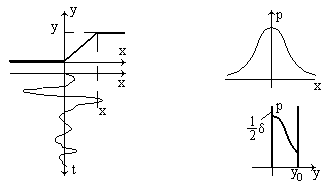
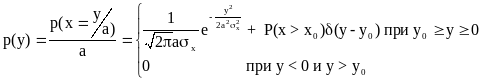
Преобразование спектра случайного процесса

в безынерционном нелинейном элементе

Непосредственно по формулам определить спектр на выходе по известному спектру на входе невозможно, нужно сначала находить корреляционную функцию на выходе и применить обратное преобразование Фурье.

Если на входе есть нелинейная функция, то можно найти ее ковариационную функцию:

. Если известна двумерная плотность вероятности входного процесса, то: .

Этот интеграл довольно трудно вычислять, поэтому прибегают к различным упрощениям.

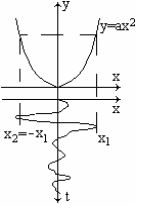
Пример: пусть у=ах². Двумерная плотность вероятности процесса x(t) равна:

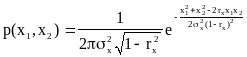, где r_x=r_x(t) – нормированная корреляционная функция входного процесса.

Проделав необходимые преобразования и использовав соотношение прейдем к выражению: .

Пусть x(t) узкополосный процесс, тогда, учитывая, что , где r₀ – огибающая корреляционной функции узкополосного процесса, запишем окончательное выражение: .

Применим теперь прямое преобразование Фурье и получим выражение для энергетического спектра процесса на выходе элемента:

Первое слагаемое (дискретное соответствует постоянной составляющей выходного колебания, второе – низкочастотной составляющей спектр которой примыкает к нулевой частоте, третье – высокочастотной составляющей со спектром, группирующимся вблизи частоты 2w₀.

Вывод: Спектр на выходе существенно отличается от спектра на входе и имеет 3 составляющих.