Прохождение случайного сигнала через линейные цепи с постоянными параметрами

Если на входе цепи действует случайный процесс с нормальным законом распределения, то на выходе получим случайный процесс имеющий нормальный закон но с уменьшенными корреляционными и спектральными характеристиками. При другом распределении на входе цепи отыскание распределения на выходе представляет собой сложную задачу.

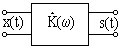
Анализ передачи нормальных процессов через линейные цепи по существу сводится к корреляционному или спектральному анализу.

Спектральная характеристика мощности и корреляционная функция случайного процесса на входе цепи

Если есть к-ая реализация на интервале Т Х_КТ(t), то мы можем найти ее спектр Х_КТ(w). Тогда на выходе цепи будет: .

По теореме Парсеваля:

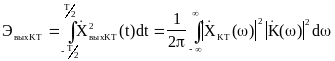
Определим спектральную плотность мощности на выходе цепи:

Вытекает следующее соотношение: . Возведение передаточной функции в квадрат объясняется тем, что она определяет отношение напряжений (токов) на входе и выходе, а W(w) является спектральной плотностью мощности случайной функции.

Корреляционная функция случайного процесса на выходе цепи:

Корреляционная функция входного сигнала:

Корреляционная функция импульсной характеристики:

Следовательно, произведению спектральных функций W(w) и K(w) соответствует свертка функций R_вх(t) и R_g(t): . Отсюда, зная корреляционные функции R_вх(t) и R_g(t) можно найти энергетический спектр: .

Пусть на входе белый шум (спектральная плотность равна 1 на всех частотах), следовательно: , так как . Тогда:

Следовательно, если мы знаем вид корреляционной функции импульсной характеристики то вид R_вых(t) имеет такой же вид.

Гармонические колебания со случайной амплитудой

Пусть имеется случайный процесс . Будем считать, что передаваемое сообщение содержится в огибающей.

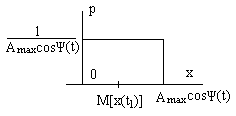
Пусть A(t) – стационарный, эргодический случайный процесс, y(t) – детерминированный процесс.

Для каждого момента времени .

Плотность вероятности величины х при заданном времени t: , при этом считается, что А распределено равномерно от 0 до А_max.

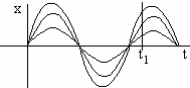
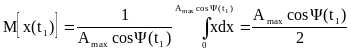
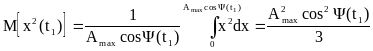
и математическое ожидание и дисперсия зависят от времени, т. е. процесс не стационарный.

Гармонические колебания со случайной фазой

Фаза обычно распределена по равномерному закону: .

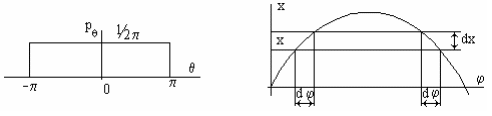
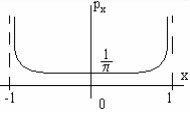
Имеется случайный процесс . Найдем закон распределения фазы

Вероятность того, что х пребывает в интервале dx равна плотности распределения на интервале

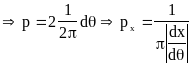
при

где

Математическое ожидание:

или

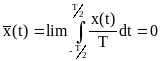
Перемножим 2 значения в разные моменты времени:

Математическое ожидание от произведения:

, где

Процесс x(t) является стационарным так как корреляционная функция зависит только от разности времени t₁ и t₂, а так же от самого времени.

Гармоническое колебание со случайной фазой является стационарным и эргодическим процессом. Гармонические колебания со случайной фазой и случайной амплитудой образует стационарный но не эргодический процесс.

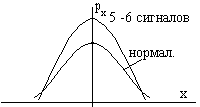
При суммировании нескольких гармонических колебаний (5 -6) со случайной фазой мы получим стационарный случайный процесс близкий к гаусовскому.