15. Многокутники. Площа мн-ка .Th існування та єдиність

О: простим мн-ком наз замкнена ламана яка не має само перетинів. Іноді під простим мн-ком розуміють частину пл. яку обмежує ця ламана.

О:простий мн-к наз орієнтованим (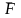 ) якщо на ньому задано орієнтацію його межі (напрямок обходу вершин).

О: х-кою мн-ка наз величина

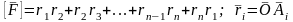
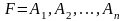
О: відобр наз ф-єю вимірювання S мн-ка якщо викон умови:

1)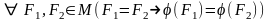 ;2)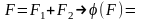

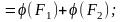3) якщо F – одиничний квадрат 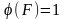. Число 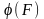наз площею мн-ка.

Т: хочаб 1 ф-ція вимірювання площі мн-ків. Дов Розгл відобр 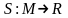де М – м-на усіх простих мн-ків площ таких що 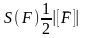. Покажемо що відобр S Відповідає означ ф-ції вимірювання площі а)

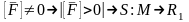
б) нех F₁ та F₂ рівні мн-ки. Причому , де -рух. Зафіксуємо репер R і нех R’= .Тоді вершини F₁ і F₂ матимуть у реперах R та R’ відповідні коорд. Х-ки F₁ та F₂ будуть рівними, а отже будуть рівними S(F₁) S(F₂) в) нех F=F₁+F₂ тоді 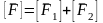.Вибиремо орієнтацію мн-ків так щоб х-ки були додатні. Перейшовши до абсол величин одержимо 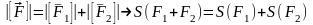.Розгль одиничн квадрат ABCD і виберемо ДСК, початок т.А а базисні вектори 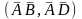тоді

т.А(0,0); В(1,0); С(1,1); D(0,1). Х-ка квадрата =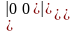 .Доведено.

Т: лише 1 ф-ція вимірювання площі мн-ків.

Лема 1: яка б не була ф-ція S вимірювання площі мн-ків для прямокутника зі сторон x,y S=xyЛема 2: яка б не була ф-ція вимірювання площі мн-ків площа трикутника з основою a та висотою h = ½ a*h Дов припустимо що хоча б 2 ф-ції вимірювання площі S,S^* тоді мн-к

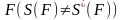
Розіб’ємо мн-к F на 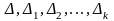з основами а₁,а₂,…,а_к і висотами

h₁,h₂,…,h_k до цих основ відповідно. Тоді 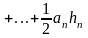.Аналогічно

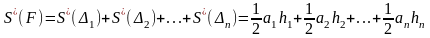
Але тоді S(F)=S^*(F) що супереч припущ Теорему дов.

О: мн-ки які мають рівну площу наз рівновеликими.

О: 2 мн-ки наз рівно складеними якщо існують такі розбиття цих мн-ків на частини що частини 1-го розбиття відповідно = частинам 2-го розбиття. Т: Будь-які рівно складені мн-ки є рівновеликими.

Т: будь-які 2 рівновел мн-ки є рівно складени

16. Геометричні побудови на пл. Система постулатів побудов.

Суть задачі на побуд полягає в тому що на основі сукупності заданих фігур потрібно побуд фігуру, яка задов умовам задачі. При цьому традиційно використ циркуль та лінійку. Аксіоми: 1. через будь-які 2 т. можна провести пр 2. можна побуд т. перетину 2-ох не // пр. 3. можна побуд коло з центром в заданій т. і радіусом рівним заданому відрізку. 4. можна побуд точки перетину 2-ох кіл якщо ці т. існують. 5. можна побуд точки перетину кола і пр якщо ці точки існують. Найпростіші побудови: 1) відкладання відрізка рівного даному від поч. заданої півпр.2) поділ відрізка пополам 3) побуд кута рівного даному 4) поділ кута пополам 5) побуд перпенд до заданої пр

6) побуд пр // до даної Метод ГМТ: нех А основний елемент побудови. Припуст що А задов якимсь 2-ом власт які визначають ГМТ: Ф₁,Ф₂ причому ці ГМТ допускають побудову циркулем та лінійкою. Очевидно 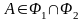т.т. ключовий елемент визначається відповідним ГМТ. Метод геометр перетворень: за допомог цього методу малюють фігуру (допоміжну) у якої певними перетвореннями (рухи, інверсія) одержують шукану фігуру. Різновидом цього методу є метод подібності: суть полягає в тому що відкидаючи 1-ну з умов задачі залишають лише ті які визначають шукану фігуру з точністю до подібності. Далі використ перетвор подібності одержують потрібні розміри а отже і шукану фігуру. Алгебр метод: полягає в тому що виділяють ключовий ел побудови – відрізок х , виражають х через задані відрізки і виконують відповідну подудову, при цьому побудову розбивають на кроки які є основними побудовами.