7.5. Планирование полного факторного эксперимента

 

Полный факторный эксперимент характеризуется тем, что число уровней каждого фактора равно двум. При соблюдении этого условия число N опытов, необходимых для реализации всех возможных сочетаний уровней факторов

N = 2^k,

где k - число факторов.

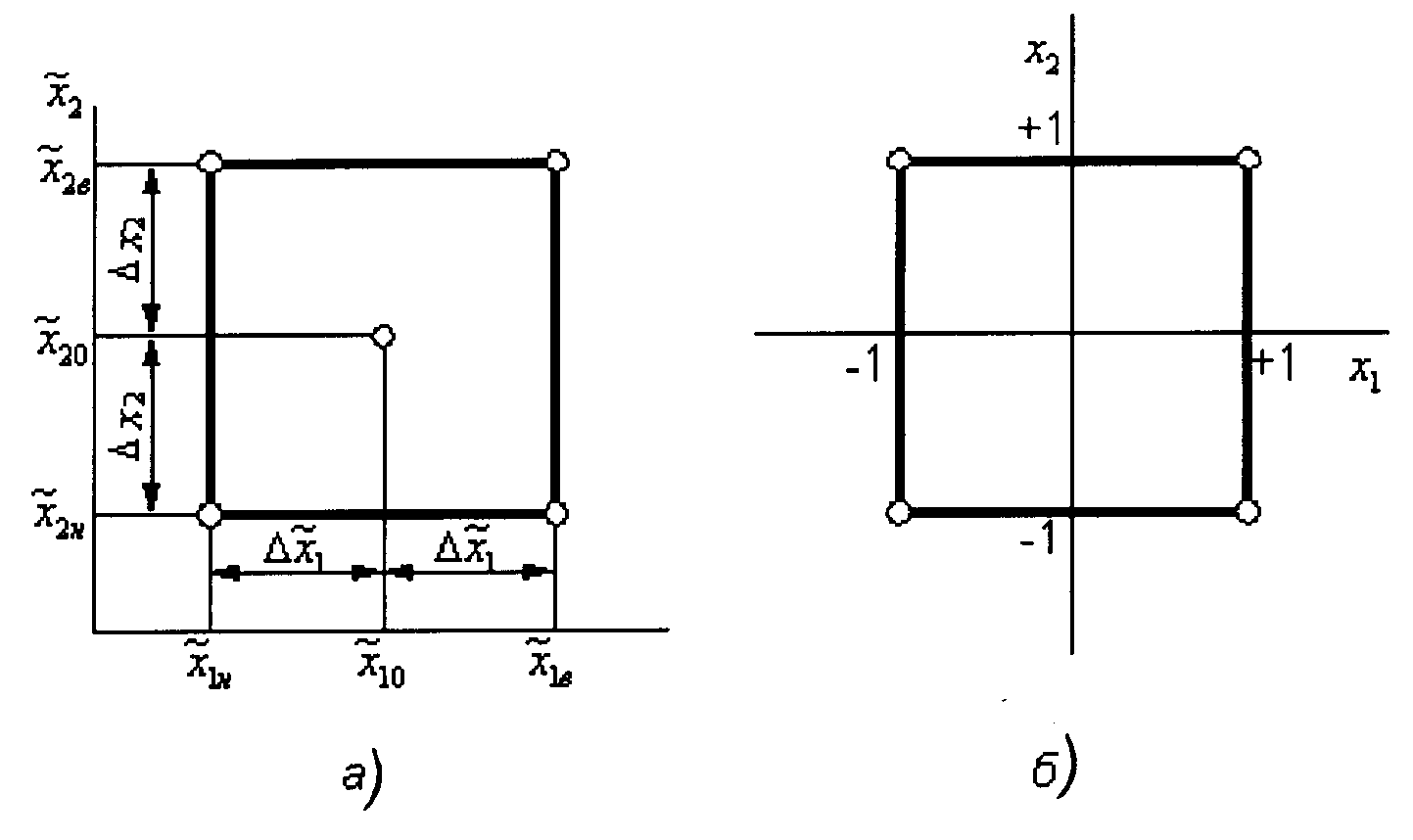
План эксперимента для двух- и трехфакторных функций отклика может быть изображен в виде графика, называемого факторным пространством. На рис.9.2 показан в факторном пространстве симметричный двухуровневый план для двухфакторной функции отклика y=f(x₁x₂) при нейтральном (рис.9.2,а) и нормированном (рис.9.2,б) представлении уровней факторов. Здесь , - искомые натуральные уровни факторов, - нижние, - верхние уровни, , - интервалы варьирования.

Рис.9.2. Симметричный двухуровневый план

для двухфакторной функции отклика

Согласно такому плану эксперимента должно быть проведено четыре опыта. Условия эксперимента также записываются в виде таблиц, называемых матрицами (репликами) планирования. Каждый столбик матрицы называют вектор-столбцом, а каждую строку – вектор-строкой (табл.9.2).

Таблица 9.2. Матрица планирования 2²

 

Номер опыта	х1	х2	y
1	-1	-1	y1
2	+1	-1	y2
3	-1	+1	y3
4	+1	+1	y4

 

При построении матрицы 2² комбинации уровней находятся прямым перебором. Если количество факторов более двух, используют три приема перехода от матрицы меньшей размерности к матрицам большей размерности.

При выполнении первых двух приемов сначала строится матрица 2², а затем – матрица 2³ (табл.9.3) и большей размерности.

Таблица 9.3. Матрица планирования 2³

 

Номер опыта	х1	х2	х3	у
1	-1	-1	-1	у1
2	+1	-1	-1	у2
3	-1	+1	-1	у3
4	+1	+1	-1	у4
5	-1	-1	+1	у5
6	+1	-1	+1	у6
7	-1	+1	+1	у7
8	+1	+1	+1	у8

 

Первый прием основан на том, что при добавлении нового фактора каждая комбинация уровней, имеющихся в матрице меньшей размерности, в матрице большей размерности встречается дважды: в сочетании с нижним и верхним уровнями нового фактора. Поэтому сначала описывается исходный план для одного уровня фактора, а затем он повторяется для другого уровня (см. табл. 9.3).

Второй прием основан на построчном перемножении двух столбцов согласно правилу знаков: одноименные знаки перед единицей при перемножении дают +1, разноименные - -1. После перемножения получается вектор-столбец произведений х₁х₂ в исходном плане. Затем исходный план продлевается по числу опытов вдвое путем повторения предыдущего исходного плана (включая столбец х₁х₂). Далее удлиненный вдвое исходный план вновь повторяется, но вместо столбца произведений записывается столбец добавленного фактора х₃ с изменением на противоположные знаки столбца х₁х₂. Этот прием несколько сложней, чем первый.

Третий прием основан на правиле чередования знаков. В матрице, включающей 2^к опытов, знаки первого столбца меняются поочередно, знаки второго столбца - через два, третьего - через четыре, четвертого - через восемь и т.д. по степеням двойки.

Матрица планирования эксперимента обладает четырьмя общими свойствами. Два свойства относятся к особенностям построения вектор-столбцов и следуют непосредственно из правил построения матрицы.

Первое свойство - симметричность относительно центра эксперимента – проявляется в правиле: алгебраическая сумма элементов вектор-столбца каждого фактора равна нулю, т.е. , где j - номер фактора, i - номер опыта, N - число опытов.

Второе свойство (условие нормировки): сумма квадратов каждого столбца равна числу опытов, т.е. .

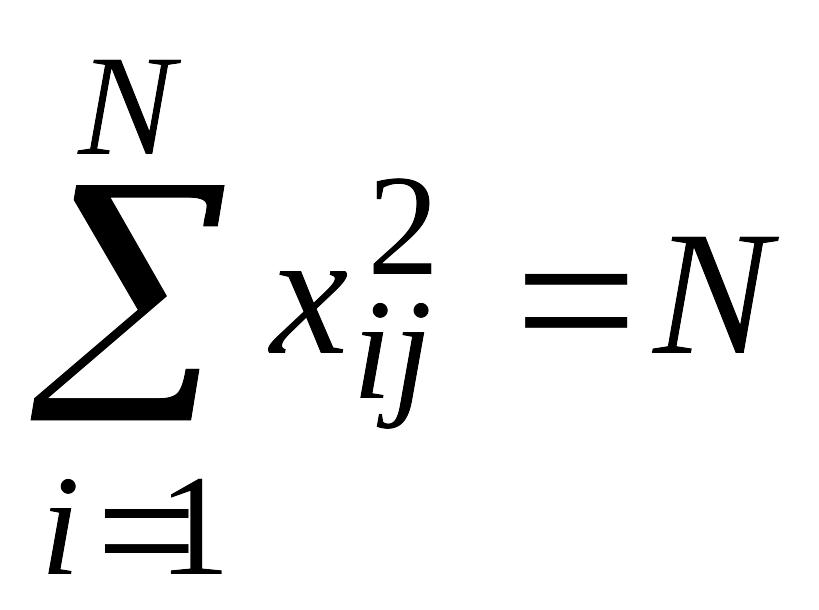Два других свойства относятся к совокупности столбцов матрицы.

Третье свойство (ортогональность матрицы): сумма почленных произведений любых двух вектор-столбцов матрицы равна нулю, т.е. 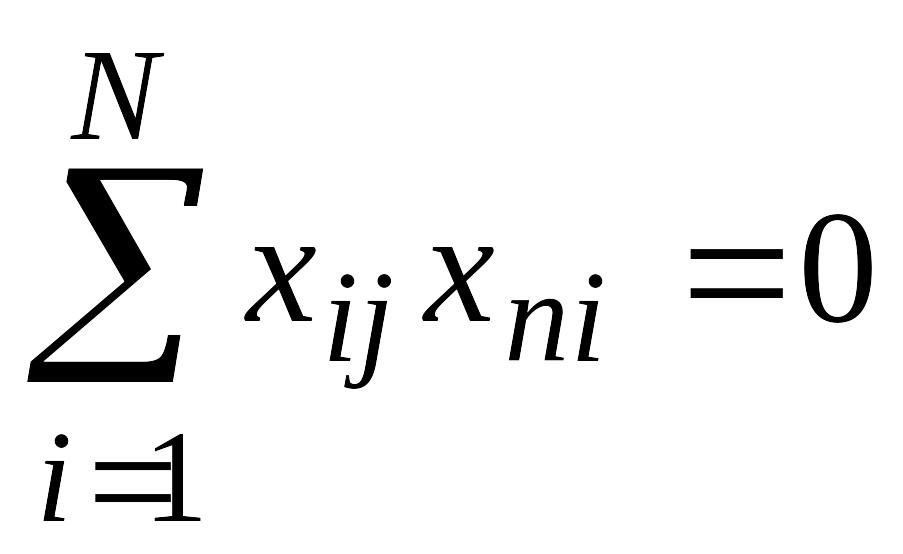, j¹n.

Четвертое свойство (ротабельность): точки в матрице планирования подбираются так, что точность предсказаний значений выходного параметра на основании математической модели одинакова на равных расстояниях от центра эксперимента и не зависит от направления.

Если матрица обладает всеми четырьмя свойствами, то она составлена правильно.

Рассмотрим вопрос об оценке коэффициентов линейной модели, считая, что задачей эксперимента является проверка гипотезы об адекватности модели

у_и = a_0и + a_1и x₁ + a_2и x_2.

Индекс и обозначает истинное значение неизвестной.

Поскольку эксперимент содержит конечное число опытов, то после их проведения можно получить только оценки для коэффициентов модели

y = a₀ + a₁ x₁ + a₂ x₂.

После проведения опытов неизвестными величинами в этом выражении будут только коэффициенты a₀, a₁, a₂. Для N опытов можно составить систему линейных условных уравнений. После ее решения методом наименьших квадратов определяются оценки коэффициентов:

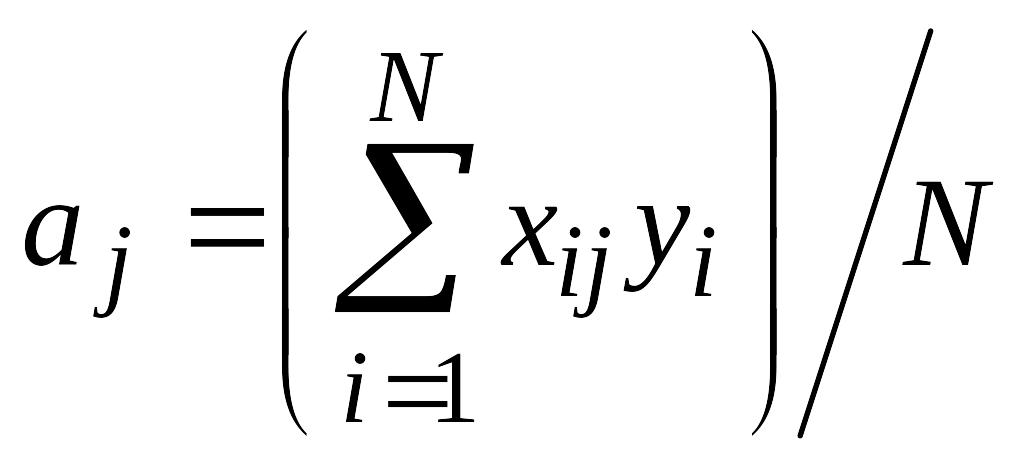. (9.8)

Так, при N=4 получим:

a₁ = [(-1)y₁ + (+1)y₂ +(-1)y₃ +(+1)y₄] / 4;

a₂ = [(-1)y₁ + (-1)y₂ +(+1)y₃ +(+1)y₄] / 4.

Для определения а₀ представим среднее значение в виде

.

Так как матрица обладает свойством симметрии, то , поэтому .

Для того чтобы получить возможность определения а₀ по формуле (9.8), в матрицу вводят фиктивную переменную х₀, которая во всех опытах принимает значение +1. Составленная линейная модель несколько видоизменяется:

у= a₀ х₀ + a₁ x₁ + a₂ x_2.

Положительные коэффициенты при х_ji пропорциональны степени влияния факторов, отрицательные - обратно пропорциональны.

Линейная модель не всегда в полной мере описывает объект исследования. Часто нелинейность связана с взаимным влиянием факторов, и задачей полного факторного эксперимента является установление степени такого взаимодействия. Для этого перемножением столбцов матрицы получают новый столбец произведений двух факторов так, что матрица размерности 2² будет иметь вид, представленный в табл.9.4.

 

 Таблица 9.4. Матрица планирования эксперимента 2² с учетом взаимодействия факторов

 

Номер опыта	х0	х1	х2	х1х2	у
1	+1	-1	-1	+1	у1
2	+1	+1	-1	-1	у2
3	+1	-1	+1	-1	у3
4	+1	+1	+1	+1	у4

С учетом взаимодействия факторов х₁х₂ видоизменяется модель

у= a₀ х₀ + a₁ x₁ + a₂ x₂ + а₁₂х₁х₂. (9.9)

Коэффициент а₁₂ вычисляется также по формуле (9.8):

a₁₂ = [(+1)y₁ + (-1)y₂ +(-1)y₃ +(+1)y₄] / 4.

Чем больше факторов, тем больше число возможных взаимодействий. Так, в матрице планирования 2³ появляются новые вектор-столбцы х₁х₂, х₁х₃, х₂х₃ , характеризующие эффект взаимодействия первого порядка, и столбец х₁х₂,х₃ , - эффект взаимодействия второго порядка. В общем случае эффект взаимодействия максимального порядка имеет порядок на единицу меньше числа факторов. Применяются также такие понятия, как парные эффекты взаимодействия (х₁х₂, х₁х₃, х₂х₃), тройные (х₁х₂х₃, х₃х₄х₅) и т.д.

Суммарное количество коэффициентов (в том числе а₀, линейные эффекты и эффекты взаимодействия) равно числу опытов, проводимых согласно матрице эксперимента. Значения различных коэффициентов независимы друг от друга.

Если модель включает не только линейные эффекты и эффекты взаимодействия, но и квадраты, кубы и т.д. факторов, то подход к оценке коэффициентов несколько иной.

Если, например, при двухфакторном эксперименте заметное влияние имеет квадратичный член, то модель можно записать следующим образом:

у= a₀ х₀ + a₁ x₁ + a₂ x₂ + а₁₂х₁х₂ + а₁₁х²₁ + а₂₂х²₂ . (9.10)

Если мы захотим построить матрицу планирования эксперимента с добавлением вектор-столбцов х²₁ и х²₂, то получим единичные столбцы, совпадающие друг с другом и со столбцом х₀, в результате чего невозможно определить, за счет чего получилось значение а₀. Полученную для такого случая оценку а₀ называют смешанной, так как она определяется совместными вкладами свободного и квадратичных членов. Соответствующая запись выглядит следующим образом:

.

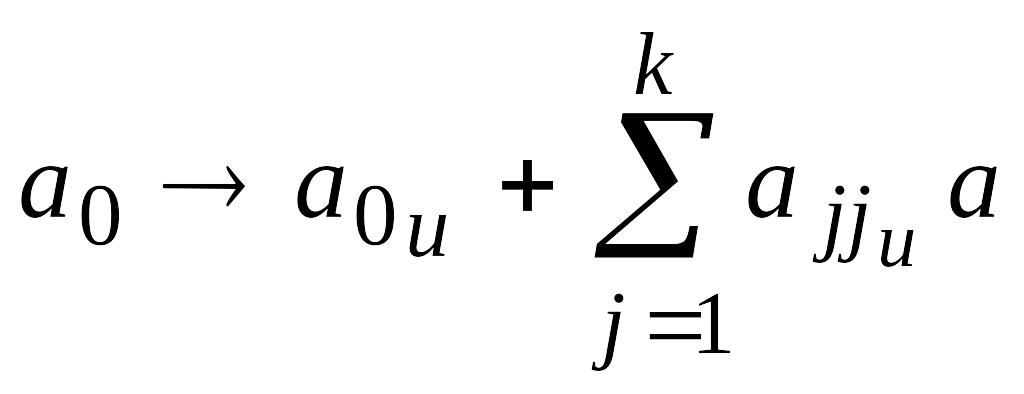Для модели (9.10) получается система, состоящая из смешанных и несмешанных оценок:

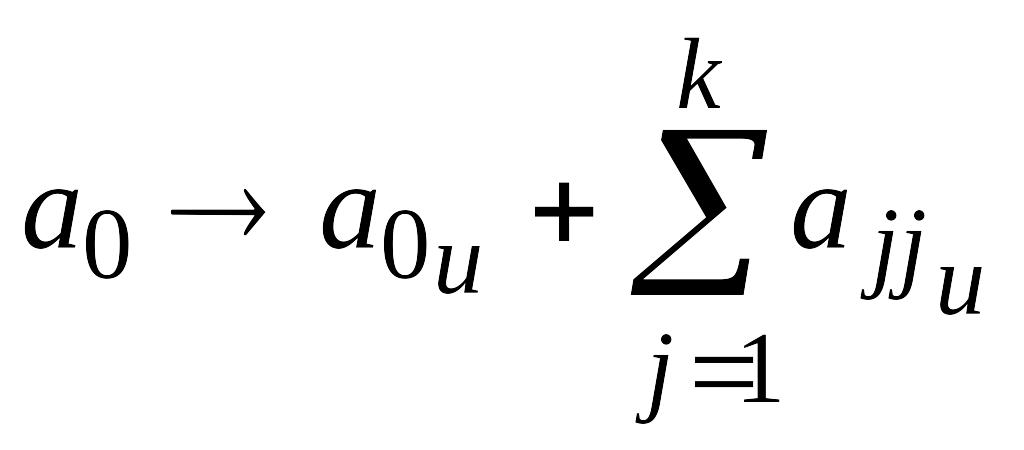; a₁® a_1и; a₂® a_2и; a₁₂® a_12и .

Итак, полный факторный эксперимент при варьировании факторов на двух уровнях позволяет оценить линейные эффекты эксперимента.