
- •Лекция 7. Измерительный эксперимент: подготовка и проведение
- •7.1. Основные этапы подготовки измерительного эксперимента
- •7.2. Общие вопросы оптимального планирования измерительного эксперимента
- •7.3. Планирование пассивного эксперимента
- •7.4. Планирование активного эксперимента
- •7.5. Планирование полного факторного эксперимента
- •7.6. Планирование дробного факторного эксперимента
- •7.7. Проведение обработки результатов эксперимента
- •7.8. Планирование эксперимента при решении задачи оптимизации методом градиента
- •Вопросы для самопроверки
7.3. Планирование пассивного эксперимента
При пассивном эксперименте существуют только факторы в виде входных контролируемых, но неуправляемых переменных, и экспериментатор находится в положении пассивного наблюдателя. Задача планирования в этом случае сводится к оптимальной организации сбора информации и решению таких вопросов, как выбор количества и частоты измерений, выбор метода обработки результатов измерений.
Наиболее часто целью пассивного эксперимента является построение математической модели объекта, которая может рассматриваться либо как хорошо, либо как плохо организованный объект. В хорошо организованном объекте имеют место определенные процессы, в которых взаимосвязи входных и выходных параметров устанавливаются в виде детерминированных функций. Поэтому такие объекты называют детерминированными. Плохо организованные или диффузные объекты представляют собой статистические модели. Методы исследования с использованием таких моделей не требуют детального изучения механизма процессов и явлений, протекающих в объекте.
Рис 9.1. График регрессионной зависимости
y от х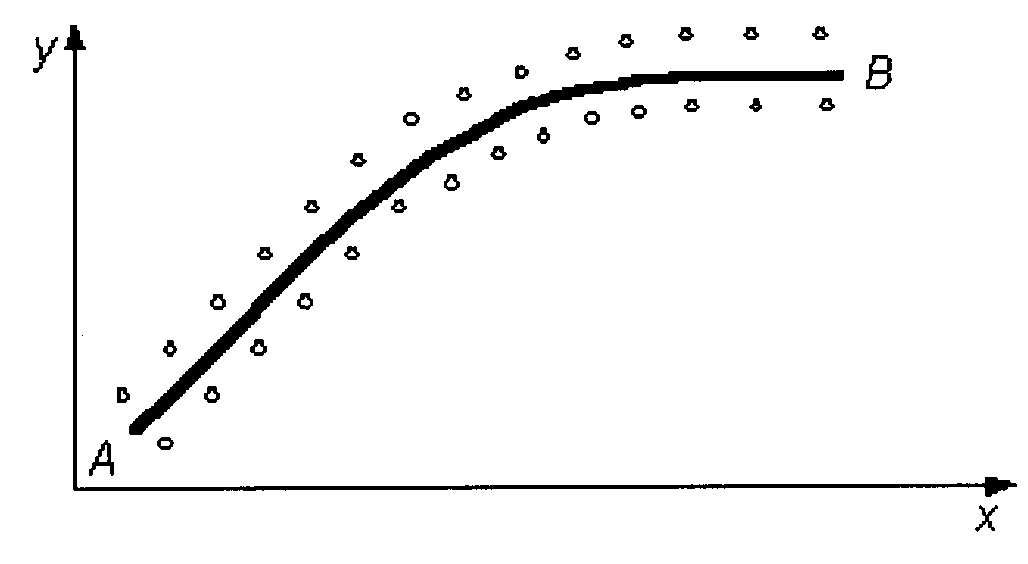
Целью однофакторного пассивного эксперимента является построение регрессионной модели. Следует отметить, что регрессионная модель является приближенной оценкой истинной регрессионной зависимости. Для построения модели следует провести обоснованный выбор аппроксимирующей функции. Критериями выбора являются простота, удобство пользования, обеспечение требуемой точности аппроксимации, адекватность. Адекватная регрессионная модель позволяет предсказывать с требуемой точностью значения выходной величины в некоторой области значений входной.
Нередко для выбора аппроксимирующей функции пользуются кривой регрессионной зависимости, проведенной "на глаз".
Чаще всего регрессионная модель представляется с помощью аппроксимирующей функцией в виде полинома
![]() .
(9.2)
.
(9.2)
Приняв такую модель, следует определиться в порядке полинома, после чего вычислить параметры а1, а2 ,…,ам., воспользовавшись методом, рассмотренным в параграфе 6.1.
В общем случае результаты измерения li значения выходной величины и ее значения yi определяемые регрессионной зависимостью от входного фактора xi, не совпадают, т.е. отлична от нуля разность Di=li-yi, что связано с наличием погрешности измерения и возмущающих воздействий. Обычно считают, что Di не зависит от значения y (т.е. аддитивна) и подчиняется нормальному закону распределения с нулевым математическим ожиданием.
Если выполнено n измерений, то их результаты можно записать в виде:
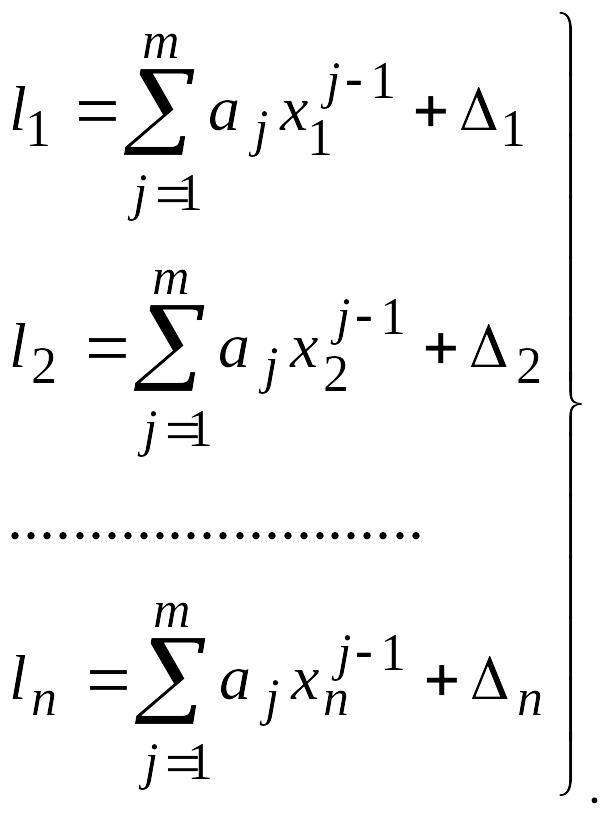 (9.3)
(9.3)
Система уравнений (9.3) линейна относительно
aj. Для
нахождения оценок aj
из условия минимума Dj
необходимо добиться равенства нулю
всех частных производных функций
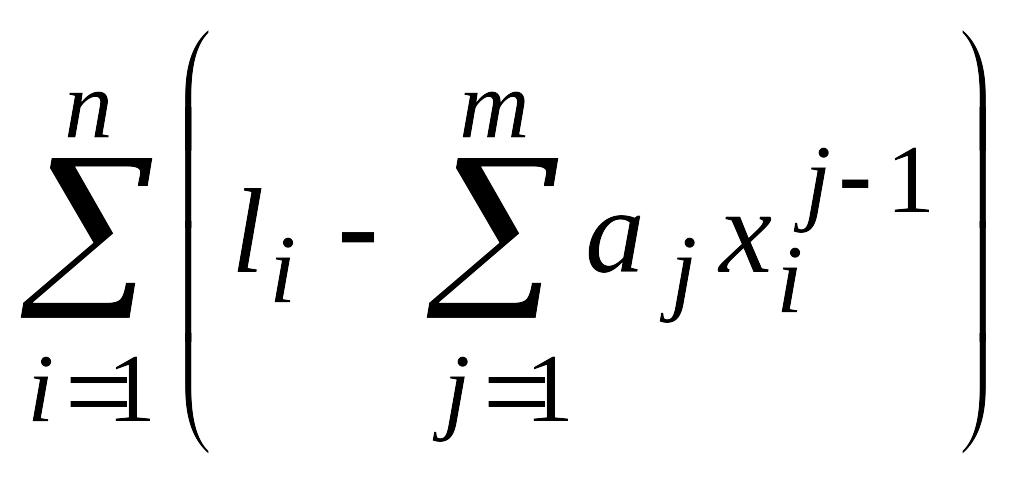 по aj. Получим
систему нормальных уравнений:
по aj. Получим
систему нормальных уравнений:
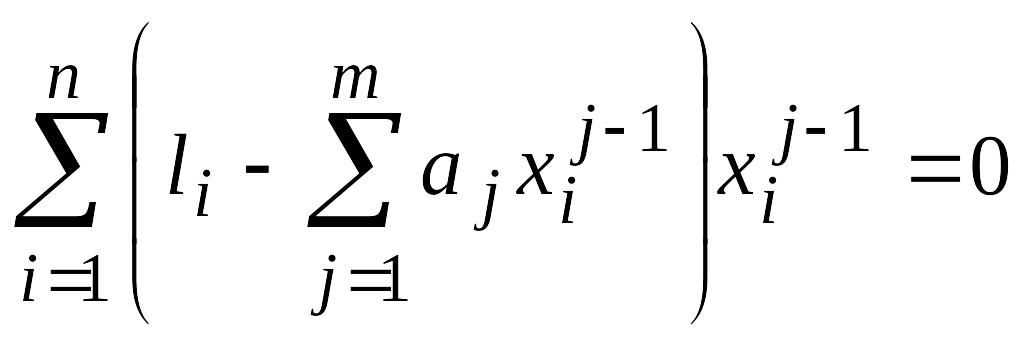 (j=1,2,…,m).
(9.4)
(j=1,2,…,m).
(9.4)
Сгруппировав все коэффициенты при неизвестных aj и записав уравнения системы (9.4) в стандартном виде можно вычислить искомые параметры aj методом определителей.
Многофакторный пассивный эксперимент дает n значений выходного параметра y объекта, соответствующих измерениям n совокупностей значений выходных параметров:
x11, x12 ,…, x1k;
x21, x22 ,…, x2k;
.……...............
xn1, xn2 ,…, xnk.,
где xij - значение j входного параметра в i-м измерении (j=1,2,...,n).
В качестве регрессионной модели примем линейный многочлен вида
у = а0 + а1х1 +a2x2+ …+ аkхk. (9.5)
Заменим переменные их центрированными значениями:
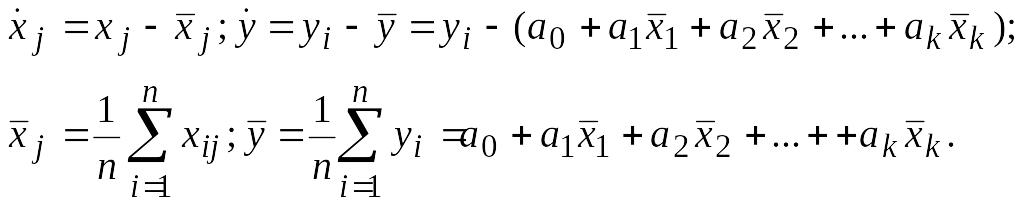
Тогда модель принимает вид
![]() .
(9.6)
.
(9.6)
На основе (9.6) составляется система
нормальных уравнений вида (9.4) (с заменой
m на k) и вычисляются
оценки параметров
![]() .
Затем вычисляется оценка
.
Затем вычисляется оценка
![]()
и осуществляется переход к исходной модели (9.5).
