2.5. Расчет параметров парной линейной регрессии
Для того, чтобы более точно выразить количественную зависимость между показателем x «Доходы» и показателем y «Расходы», необходимо построить уравнение парной линейной регрессии между двумя показателями, т.е. уравнение вида y = k0 + k1x. Для этого требуется построить вспомогательную таблицу и найти необходимые значения параметров уравнения регрессии (Приложение 10).
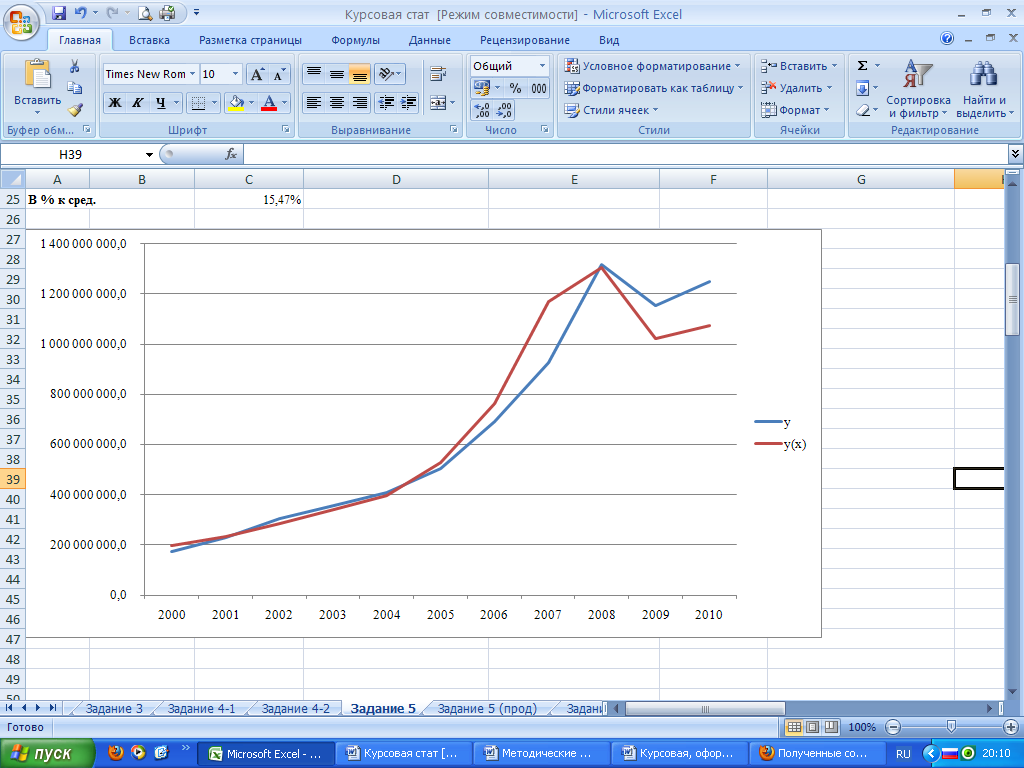
Исходные данные y и рассчитанные по уравнению регрессии значения yx можно изобразить графически (Рисунок 4).
Рисунок 4
Исходные и расчетные данные показателя y
В итоговой строке вспомогательной таблицы (Приложение 10) необходимо рассчитать соответствующие суммы. Для расчета параметров парной линейной регрессии необходимо подставить полученные суммы (Σx, Σy, Σx2, Σxy) в следующие формулы:
В результате расчетов получаем следующие значения параметров регрессии: k0 = -1 465 545,43; k1 = 1,0122.
Затем находим расчетные значения показателя y по уравнению регрессии yx в предпоследней графе вспомогательной таблицы (Приложение 10), определяем квадраты отклонений расчетных значений от фактических в последней графе таблицы, суммируем их и рассчитываем ошибку аппроксимации для данного уравнения. Далее, разделив полученную сумму на 11, и, после извлечения из нее квадратного корня, получаем ошибку аппроксимации, равную 102 836 192,26 или 15% от среднего значения y.
Чтобы более строго оценить качество построенного уравнения регрессии, обычно недостаточно рассчитать только ошибку аппроксимации. Дополнительно следует рассчитать еще дисперсию фактических и расчетных значений результативного показателя y и найти коэффициент детерминации как отношение расчетной и фактической дисперсии. Коэффициент детерминации показывает, какая доля дисперсии (т.е. колеблемости) результативной переменной x объясняется дисперсией (т.е. колеблемостью) факторного показателя y.
Для определения коэффициента детерминации необходимо осуществить следующие действия. Во-первых, находятся дисперсии расчетных и фактических значений y c помощью вспомогательной таблицы. Для расчета индекса детерминации как отношения этих двух дисперсий строится вспомогательная таблица (Приложение 11).
Сумма расчетных значений y, как и должно быть, совпадает с суммой фактических, поэтому и их средняя величина совпадает и равна 664808657,7. Вычитая эту величину из каждого фактического значения и из каждого расчетного, находим отклонения расчетных и фактических значений от их среднего значения. Затем возводим эти отклонения в квадрат и суммируем. Получаем две суммы: 1 827 914 381 497 420 000,0 и 1 711 586 274 677 870 000,0.
Разделив эти суммы на n = 11, получаем две дисперсии: дисперсию фактических значений σ2y = 166174034681584000 и дисперсию расчетных значений σ2yx = 155598752243443000. Находим их отношение и получаем коэффициент детерминации: R2 = 155598752243443000 / 166174034681584000 = 0,9364.
По результатам выполненных операций необходимо сделать следующий вывод. Ошибка аппроксимации равна 102 836 192,26, т.е. составляет примерно 15% среднего значения y, равного 664 808 657,7 (допустимо, если ошибка аппроксимации не превышает 15% от среднего значения результативного показателя). Индекс детерминации равен 0,9364, то есть очень близок к 1. Значит, построенное уравнение регрессии является значимым, то есть описывает существенную зависимость между доходами и расходами городского бюджета.