8.2 Передаточное отношение планетарной передачи

Передаточное отношение планетарной передачи определяют обычно аналитически, реже – графически. Аналитический метод (метод Виллиса) основан на том, что всей планетарной передаче мысленно сообщается дополнительное вращательное движение вокруг центральной оси с уг­ловой скоростью водила _н, но в обратном направлении. При этом водило как бы останавливается, а закрепленное центральное колесо освобождается. В результате получается так называемый обращённый механизм, представляющий собой обычную непланетарную передачу, у которой геометрические оси всех колёс неподвижны, а сателлиты превращены в промежуточные (паразитные) колеса.

В качестве примера рассмотрим приложение метода Виллиса к простейшей передаче по схеме рисунка 8.1. Пусть ведущим звеном в этой передаче является солнечное колесо 1, а ведомым – водило Н. По общему определению передаточное отношение между звеньями 1 и Н имеет вид

. (8.1)

Ставится задача выразить это передаточное отношение через известные числа зубьев колес Z₁, Z₂, Z₃.

У передачи по рисунку 8.1 звенья 1, 2, 3, Н вращаются с фактическими угловыми скоростями соответственно ₁,  ₂, ₃ = 0,  _H. Сообщим мысленно всей планетарной передаче дополнительное вращение вокруг центральной оси с угловой скоростью _H, но противоположной по направлению. Звенья полученного таким образом обращенного механизма получат угловые скорос­ти, представленные в таблице 8.1.

Таблица 8.1 – Фактические угловые скорости звеньев передачи по рисунку 8.1 и угловые скорости звеньев обращенного механизма

Номера и наименования звеньев передачи по рисунку 8.1	Фактические угловые скорости звеньев передачи по рисунку 8.1	Угловые скорости звеньев обращенного механизма
1 - солнечное колесо	1	1 – Н
2 - сателлит	 2	2 – Н
3 - корончатое колесо	3 = 0	0 – Н= – Н
Н - водило	Н	Н – Н = 0

Р ешить поставленную задачу, развивая выражение для i_1-H по формуле (8.1) непосредственно нельзя, так как в обращенном механизме _Н = 0. Поэтому для обращенного механизма (водило остановле- но !), как для обычной зубчатой передачи с неподвижными осями колес, запишем выражение передаточного отношения (см. рисунок 1.8).

Примечания

1 Индекс Н при обозначении обозначает, что передаточное отношение относится к обращенному механизму, в котором мысленно остановлено звено Н.

2 Знак минус при отношении Z₂ / Z₁ означает, что колеса 1 и 2 вращаются в разные стороны, и поэтому передаточное отноше­ние для них отрицательно.

И так, после несложных преобразований последних выражений получаем

Отсюда искомое передаточное отношение планетарной передачи по рисунку 1.8 получает вид

(8.2)

Для закрепления навыков использования метода Виллиса применим его к более сложной передаче и найдем выражение для передаточного отношения i_1-H = ₁ / _H, планетарной передачи по схеме рисунка 8.2а.

Как и в предыдущем случае, в таблице 8.2 запишем угловые скорости звеньев упомянутой планетарной передачи и звеньев соответствующей обращенной передачи (остановлено водило Н).

Таблица 8.2 – Фактические угловые скорости звеньев передачи по рисунку 8.2а угловые скорости звеньев обращенного механизма

Номера и наименования звеньев передачи по ри­сунку 8. 2а	Фактические угловые скорости звеньев пе­редачи по рисунку 8.2а	Угловые скорости звеньев обращен­ного механизма
1 – солнечное колесо	1	1 – н
2 – сателлит	2	2 – н
3 – сателлит	3 = 2	3 – н = 2 – н
4 – корончатое колесо	4 = 0	0 – н = – н
Н – водило	н	н – н = 0

Пользуясь методикой решения предыдущей задачи, запишем сначала при остановленном водиле для обращенного механизма

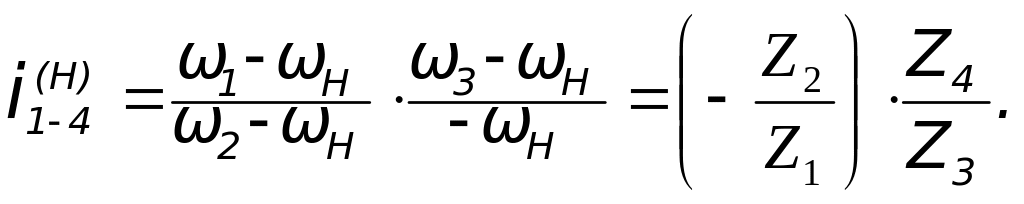
Д алее с учетом, что ₃ – _н = ₂ – _н, после преобразований получаем

Отсюда искомое передаточное отношение

(8.3)