15. Динамические системы, аксиоматика. Аксиомы переходной функции.

ДС называется конструкция, образуемая совокупностью множеств и отображений

T –упорядоченное множество моментов времени

X – множество состояний системы x вектор значений, который принимает

U – множество мгновенных значений входных величин.

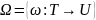
- предыстория в этот период

Множество и должно обладать свойством сочленения

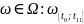
(рисунок)

Y – множество мгновенных значений выходных величин

µ - множество допустимых значений выходных величин

X

U Y

.

– переходная функция системы

– переходная ф-я система, значения которой являются состояния системы, в которых она оказывается в момент времени t, если в начальный момент времени t₀, она находилась в x(t₀) и если на неё действовало входное воздействие .

Свойство (аксиома) переходной функции:

1. Эта ф-я должна быть согласована существует некоторый момент времени t₀

2. Выполняется аксиома причинно-следственности (согласованности входных сигналов)

(рисунок)

3. Переходная ф-я обладает полугрупповым свойством (транзитивности).

(рисунок) Переход в 2 прыжка нужно брать композицию

Если известна переходная ф-я, то для непрерывной ДС малое состояние определяется следующим образом:

f(t,x,u(t)) производящая ф-я

Чаще бывают законы, которые описываются в терминах производящая ф-я.

16. Производящая функция системы. Понятия и термины, используемые в теории динамических систем. Основные виды динамических систем.

17. Структура общего решения (переходной функции) линейной динамической системы.

18. Понятие устойчивости, виды устойчивости динамических систем. Критерий асимптотической устойчивости А. М. Ляпунова.

19. Траектории динамических систем на плоскости, классификация особых точек. Странные аттракторы и квазистохастическое поведение динамических систем (динамический хаос).

; – след матрицы A;

Посмотрим на корни этого уравнения:

№	Тип собственных значений		Тип особой точки	Вид фазовых траекторий
1	Действительные отрицательные		Устойчивый узел
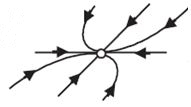
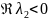
2	Действительные положительные		Неустойчивый узел
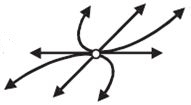
3	Комплексные с отрицательной действительной частью		Устойчивый фокус
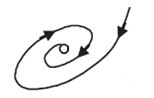
4	Комплексные с положительной действительной частью		Неустойчивый фокус
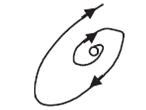
5	Действительные разных знаков		Седло
6	Чисто мнимые		Центр