§ 5. Метод прогонки.

Рассмотрим линейное дифференциальное уравнение (1)¹ с двухточечными линейными краевыми условиями (2). От дифференциального уравнения (1) обычным приемом переходят к конечно- разностным уравнениям. Для этого разобьем отрезок [a; b] на n равных частей с шагом Полагая; и вводя обозначения:

p_i = p(x_i), q_i = q(x_i), f_i = f(x_i), y_i = y(x_i), получаем при x ₌ x_i вместо дифференциального уравнения (1) следующее конечно-разностное уравнение

Отсюда после упрощения будем иметь:

(3),

Введя обозначения: будем иметь:

(i = 0, 1, 2, …, n – 2) (4),

причем из краевых условий (2) имеем

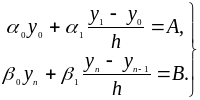(5).

Линейная система (4),(5) состоит из n + 1 уравнений относительно n + 1 неизвестных Эту систему можно решить обычным способом. Однако существует более короткий.

Разрешая уравнение (4) относительно y_i+1,находим:

(6).

Предположим, что с помощью полной системы (4) из уравнения исключен член, содержащий y_i. Тогда уравнение (6) может быть записано в виде:

(7),

где коэффициенты подлежат определению . Найдем формулы для этих коэффициентов. При i=0 из формулы (6) и краевых условий (5) следует, что:

Исключая отсюда y, будем иметь: Разрешая это уравнение относительно y₁, будем иметь: 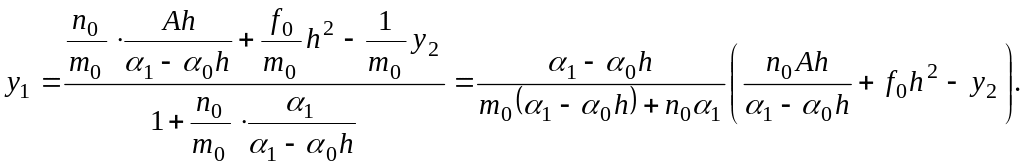(8).

Но согласно формуле (7) имеем:

(9).

Отсюда, сравнивая формулы (8) и (9), находим:

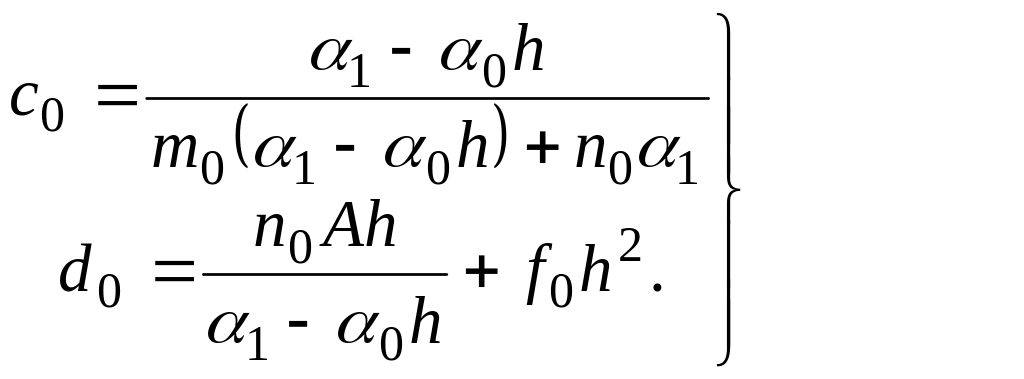(10).

Пусть теперь i>0 (i=1,2,.....n-2). Выражая y_i по формуле (7), получим: Подставляя это в (6), имеем: Разрешая это относительно y_{i + 1} будем иметь: 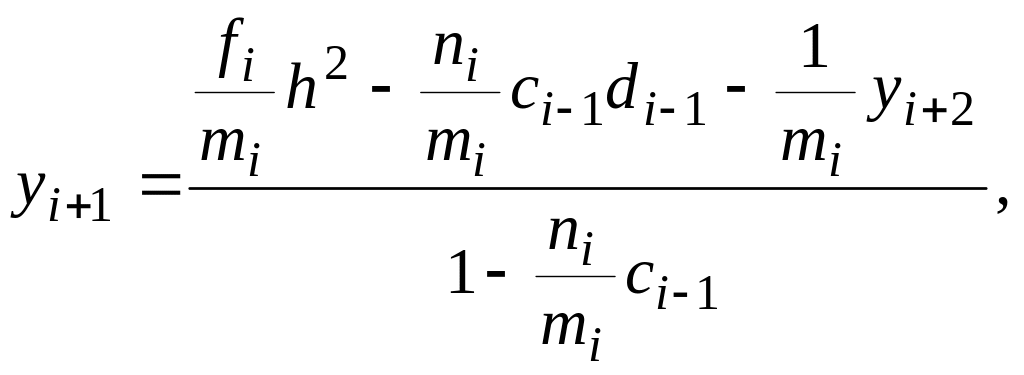или:

(11).

Отсюда, сравнивая формулы (7) и (11), получаем для коэффициентов С_i и D_i рекуррентные формулы:

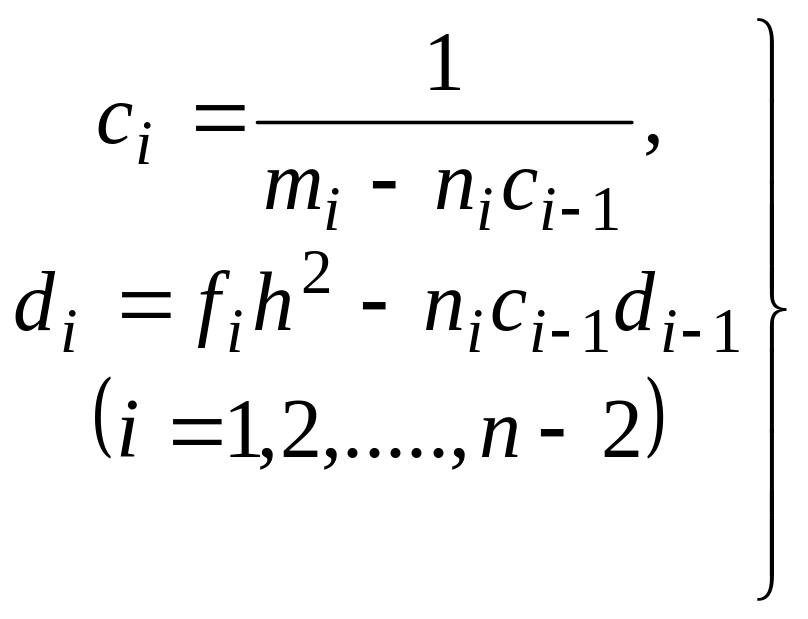(12).

На основании формул (12), используя формулы (10) для С₀ и D₀, можно последовательно определить коэффициенты Сi и Di (i=1, 2, ...,n - 2) до С_n-2 и D_n-2 включительно (прямой ход). Из формулы (7) при i = n - 2 и второго краевого условия (5) получаем:

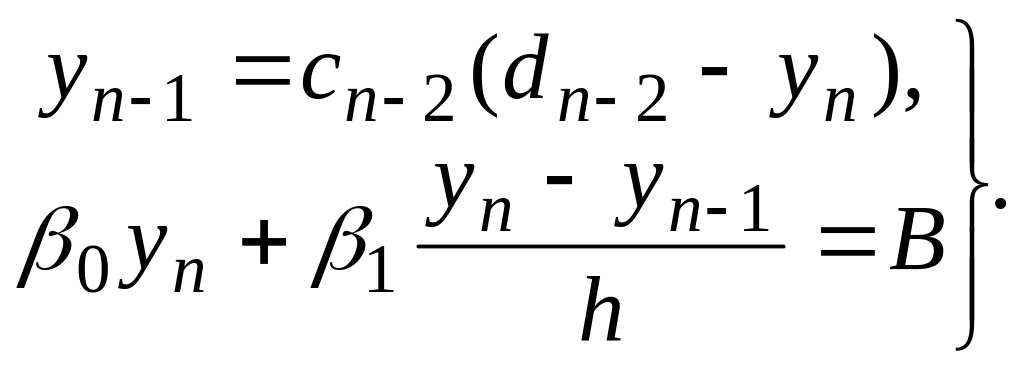
Теперь используя формулу (7) и первое краевое условие (5), мы можем последовательно найти y_n-1, y_n-2, ..., y₀ (обратный ход).

§6. Программы.

1. Метод сведения к задаче Коши.

#include <stdio.h>

#include <conio.h>

#include <math.h>

#define p(x) (-3*(x))

#define q(x) (-4)

#define r(x) (1)

#define N 500

#define EPS 0.0001

void runge_kutt (void);

int n;

double y[N];

double a=1, b=1.6, A=-3.3, B=-2;

double h=0.06, x;

main ()

{

int i, t;

double y1[N], eps[N], max_eps;

for (i=0;i<N;i++) y1[i]=0;

clrscr ();

do

{

for(i=0;i<=n;i++) y1[i]=y[i];

n=(b-a)/h+.5;

if (n>N)

{

printf ("\n Ошибка: выход за пределы массива ");

getch ();

return 0;

}

runge_kutt ();

max_eps=0;

for (i=0;i<=n/2;i++)

{

eps[i]=fabs(y[2*i]-y1[i]);

if (eps[i]>max_eps) max_eps=eps[i];

}

h/=2;

}

while (max_eps>EPS);

clrscr ();

printf (" Решение краевой задачи дли дифференциального уравнения \n\

II- порядка с точностью Е = %методом сведения к задаче Коши \n\n",EPS);

printf ("ЙНННННННННННННЛННННННННННННННННННННННЛННННННННННННННННННН»\n");

for (i=0;i<=n/2;i+=(0.06/(h*4)+0.06))

printf ("є x = %.2f є y(x) = %+f є eps = %.1e є\n",a+h*4*i,y1[i],eps[i]);

printf ("ИНННННННННННННКННННННННННННННННННННННКНННННННННННННННННННј\n");

printf ("\n Результаты представлены с шагом 0.06\n");

printf ("\заданная точность достигнута при шаге, равном %g\n",EPS,h*4);

getch ();

return 0;

}

/******************************************************************************

Функция, вычисляющая корни дифференциального уравнения II порядка методом Рунге – Кутта после сведения его к задаче Коши.

******************************************************************************/

void runge_kutt (void)

{

int i;

double u[N], v[N], z[N], g[N], x, c;

double ku1,ku2,ku3,ku4,kz1,kz2,kz3,kz4;

double tv1,tv2,tv3,tv4,tg1,tg2,tg3,tg4;

z[0]=1;

u[0]=0;

v[0]=A;

g[0]=0;

for (i=0;i<=n;i++)

{

x=a+h*i;

ku1=z[i];

kz1=-p(x)*z[i]-q(x)*u[i];

tv1=g[i];

tg1=-p(x)*g[i]-q(x)*v[i]+r(x);

ku2=z[i]+h/2*kz1;

kz2=-p(x+h/2)*(z[i]+h/2*kz1)-q(x+h/2)*(u[i]+h/2*ku1);

tv2=g[i]+h/2*tg1;

tg2=-p(x+h/2)*(g[i]+h/2*tg1)-q(x+h/2)*(v[i]+h/2*tv1)+r(x+h/2);

ku3=z[i]+h/2*kz2;

kz3=-p(x+h/2)*(z[i]+h/2*kz2)-q(x+h/2)*(u[i]+h/2*ku2);

tv3=g[i]+h/2*tg2;

tg3=-p(x+h/2)*(g[i]+h/2*tg2)-q(x+h/2)*(v[i]+h/2*tv2)+r(x+h/2);

ku4=z[i]+h*kz3;

kz4=-p(x+h)*(z[i]+h*kz3)-q(x+h)*(u[i]+h*ku3);

tv4=g[i]+h*tg3;

tg4=-p(x+h)*(g[i]+h*tg3)-q(x+h)*(v[i]+h*tv3)+r(x+h);

u[i+1] = u[i] + (ku1+2*(ku2+ku3)+ku4)*h/6;

z[i+1] = z[i] + (kz1+2*(kz2+kz3)+kz4)*h/6;

v[i+1] = v[i] + (tv1+2*(tv2+tv3)+tv4)*h/6;

g[i+1] = g[i] + (tg1+2*(tg2+tg3)+tg4)*h/6;

}

c = (B-v[n])/u[n];

for (i=0;i<=n;i++) y[i] = u[i]*c + v[i];

}