
- •Московский авиационный институт
- •II курса группы с-208
- •§ 1. Общая постановка задачи.
- •§ 2. Метод сведения краевой задачи к задаче Коши.
- •§ 3. Метод конечных разностей.
- •§ 4. Метод Галеркина.
- •§ 5. Метод прогонки.
- •§6. Программы.
- •Метод сведения к задаче Коши.
- •Метод конечных разностей.
- •Метод Галеркина.
- •§ 7. Результаты.
- •Метод конечных разностей2:
- •Метод Галеркина.
Московский авиационный институт
(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
Курсовая работа
по численным методам
на тему: Решение дифференциальных уравнений.
Выполнил студент
II курса группы с-208
факультета «Стрела»
Шарапов Максим.
Жуковский, 2001.
Оглавление.
Курсовая работа 1
по численным методам 1
на тему: Решение дифференциальных уравнений. 1
Оглавление. 3
§ 1. Общая постановка задачи. 4
§ 2. Метод сведения краевой задачи к задаче Коши. 4
§ 3. Метод конечных разностей. 5
§ 4. Метод Галеркина. 6
§ 5. Метод прогонки. 6
§6. Программы. 8
§ 7. Результаты. 12
§ 1. Общая постановка задачи.
В курсовой работе
по численным методам требуется решить
краевую задачу для обыкновенного
дифференциального уравнения вида:
![]() Решение необходимо произвести независимо
тремя методами:
Решение необходимо произвести независимо
тремя методами:
Методом сведения краевой задачи к задаче Коши.
Методом конечных разностей.
Методом Галёркина.
Задание
(вариант № 28).
![]()
§ 2. Метод сведения краевой задачи к задаче Коши.
Пусть дано линейное дифференциальное уравнение:
![]() (1),
(1),
где функции: p(x), q(x), f(x) непрерывны. Требуется найти решение уравнения (1), удовлетворяющее краевым условиям:
![]() (2),
(2),
где:
![]() -
заданные константы, причем:
-
заданные константы, причем:
![]() и
и
![]()
Решение будем искать в виде:
y = cu + v (3),
где: u = u(x) – ненулевое решение соответствующего неоднородного уравнения:
![]() (4),
(4),
а v = v(x) – какое-нибудь решение данного неоднородного уравнения (1):
![]() (5).
(5).
Очевидно, что функция, определенная формулой (3) является искомым решением уравнения (1), где с – произвольная постоянная.
Потребуем, чтобы первое краевое условие (2) выполнялось для y при любом с. Используя его, будем иметь:
![]() или:
или:
![]() (6).
(6).
Для того чтобы последнее равенство было справедливо при любом с, необходимо и достаточно, чтобы коэффициент при с обращался в 0, т.е., было выполнено следующее:
![]() (7),
(7),
![]() (8).
(8).
Для обеспечения равенств (7-8) достаточно, например, положить:
![]()
![]() (9),
(9),
где: k – постоянная, отличная от 0;
![]()
![]() (10),
(10),
если
![]() и:
и:
![]()
![]() (11),
(11),
если
![]()
Отсюда видно, что u есть решение задачи Коши для однородного уравнения (4), удовлетворяющее начальным условиям (9), а v есть решение задачи Коши для неоднородного уравнения (5), удовлетворяющее начальным условиям (10) или (11). При этом для любого с функция y = cu + v удовлетворяет краевому условию на конце x = a.
Подберем постоянную
c так, чтобы функция y
удовлетворяла краевому условию (2) на
другом конце отрезка y
= b. Это дает:
![]() откуда:
откуда:
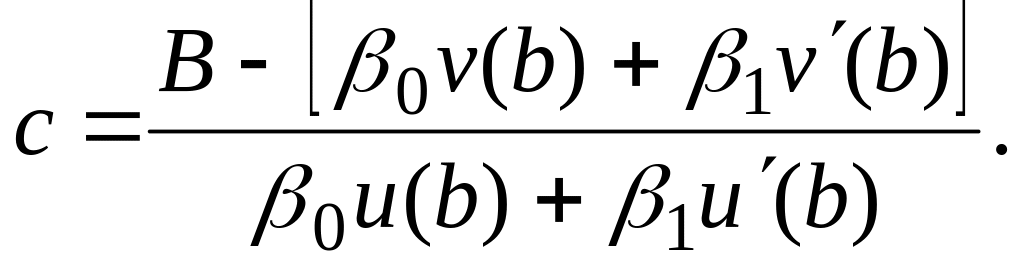 При этом предполагается, что знаменатель
этого выражения отличен от нуля:
При этом предполагается, что знаменатель
этого выражения отличен от нуля:
![]() (12).
(12).
Таким образом, краевая задача (1-2) сведена к двум задачам Коши для функций u(x) и v(x).
Замечание 1. Если выполнено условие (12), то краевая задача (1-2) имеет единственное решение. Если же условие не выполняется по каким-либо причинам, то исходная задача может либо –вообще не иметь решений, либо их бесчисленное множество.
Замечание
2. Если исходное уравнение
(1) является однородным, т.е.: f(x)
0, и
кроме того, A = 0, то в
силу условий (10) или(11) имеем:
![]() т.е., v
0. Поэтому: y = cu(x),
где u(x)
– решение уравнения (4), удовлетворяющее
начальным условиям (9). Очевидно, в этом
случае:
т.е., v
0. Поэтому: y = cu(x),
где u(x)
– решение уравнения (4), удовлетворяющее
начальным условиям (9). Очевидно, в этом
случае:
![]()
