Системы уравнений
Задание и решение систем уравнений. Функция solve. Решение систем, содержащих линейные уравнений и полиномы. Примеры для начального уровня: Уравнения прямой и окружности. Аналитическое решение системы двух линейных уравнений. Графическая иллюстрация решения. Решение системы двух (не обязательно линейных) уравнений. Решение задач с использованием систем уравнений. Графическая иллюстрация получаемых решений (в соответствии с рисунком 11).
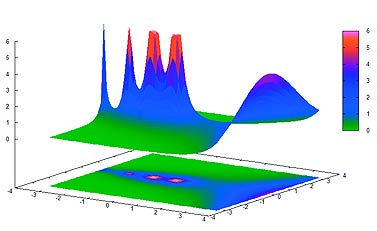
Рисунок 11 - График модуля гамма-функции на комплексной плоскости в районе 0
Тригонометрические и геометрические задачи
В Maxima реализован весьма совершенный механизм векторно-матричных операций, позволяющий проводить сложные алгебраические вычисления. Матрицы вводятся универсальным оператором matrix, затем к ним применимы обычные линейные операции -- сложение, вычитание, умножение на скаляр (для их записи используют естественную математическую нотацию вроде A+B), а также транспонирование, обращение, вычисление определителей, спектральных характеристик и пр.
Координаты точки на плоскости. Изображение точек на графике по их координатам. Векторы. Треугольники и другие многоугольники. Использование графических возможностей СКМ для изображения отрезков и многоугольников. Тригонометрические функции в Maxima, упрощение тригонометрических выражений (в соответствии с рисунком12).
Рисунок 12 – Представление окна программы Maxima с тремя задачками из курса школьной алгебры
1.3. Применение программы Maxima для решения задач высшей математики
1. Стандартные функции в составе Maxima. Перечень и особенности встроенных математических функций.
2. Символьное вычисление выражений.
Подробный анализ команды ev. Флаги управления вычислением. Выбор части выражения. Анализ выражений. Выделение коэффициентов. Работа со списками. Специальные функции для работы с выражениями (mapping functions). Подстановки (substitution). Функции assume, at, atvalue и т.п. Флаги управления подстановкой. Упрощение, расширение (expand) и факторизация (factor) выражений. Упрощение различных типов выражений (рациональных, тригонометрических, логарифмических и экспоненциальных, содержащих факториал). Функции trigsimp, trigexpand, trigreduce, ratsimp, radcan. Преобразование полиномов, отыскание наибольшего общего делителя или кратного. Флаги управления преобразоби.ванием выражений.
3. Задачи линейной алгебры.
Создание массивов и операции с ними. Создание матриц. Базовые операции с массивами и матрицами. Специальные матрицы. Манипулирование матрицами (добавление/удаление строк, столбцов и т.п.). Обращение матриц, приведение к треугольной форме, транспонирование, вычисление характеристического полинома, определителя. Собственные числа и собственные векторы. Решение систем линейных уравнений в матричной форме. Факторизация матриц. Ранг матрицы.
4. Решение уравнений и их систем.
Решение алгебраического уравнения. Функции solve(exp, var) и FUNCSOLVE (eqn, g(t) ). Решение линейных систем. Функция LINSOLVE ([exp1, exp2, . . . ], [var1, var2, . . . ] ) Вычисление корней полиномов. Функция ALLROOTS (poly). Интерполяция и отыскание нулей функции. Функции INTERPOLATE (fun, var, a, b) и NEWTON (exp, var, X0, eps). Операции с рядами. Операция суммирования, флаги управления ею. Вычисление произведений (команда PRODUCT).
5. Основные операции математического анализа.
Предел и непрерывность функции. Вычисление пределов. Правило Лопиталя. Дифференцирование функций одной пиеременной. Функция diff. Дифференцирование функций, заданных параметрически. Графики функций. Уравнения касательной и нормали. Асимптоты. Исследование функции, отыскание нулей первой и второй производной. Дифференцирование функций нескольких переменных. Дифференциальные операторы. Интегрирование. Функции integrate(expr,x), integrate(expr,x,a,b). Неопределенный интеграл. Способы интегрирования, замена переменных. Определенный интеграл. Задачи, приводящие к определенному интегралу (геометрические, технические и т.п.). Числовые и степенные ряды. Ряды Тейлора и манипулирование ими. Аппроксимация Падэ. Бесконечные дроби. Классические ряды Фурье. Интграл и преобразование Фурье. Вычисление прямого и обрабного преобразования Лапласа. Примеры задач.
6. Решение дифференциальных уравнений в Maxima.
Типы задач, связанных с ОДЕ. Задача Коши, граничная задача. Аналитические методы решения и типы ОДЕ. Задание ОДЕ в Maxima. Функции, используемые для решения ОДЕ (bc2, ic1, ic2, desolve, ode2). Решение линейных систем. Особенности решения различных типов уравнений. Решение интегральных уравнений. Функция IEQN (ieqn, unk, tech, n, guess).