57 стр. Простейшая задача вариационного исчисления. Уравнение Эйлера

Лабораторная работа №10

Тема: Простейшая задача Вариационного исчисления. Уравнение эйлера

Цель работы: Ознакомиться с простейшей задачей вариационного исчисления и уравнением Эйлера, овладеть методикой решения экстремальных задач в функциональных пространствах.

1. Основная задача вариационного исчисления

Пусть функция имеет непрерывные частные производные по всем аргументам до второго порядка включительно. Среди всех функций y(x), имеющих непрерывную производную и удовлетворяющих граничным условиям:

y(a)=A, y(b)=B. (1)

Найти функцию, которая доставляет слабый экстремум функционалу

. (2)

Другими словами, простейшая задача вариационного исчисления состоит в отыскании слабого экстремума функционала вида (2) на множестве всех гладких кривых, соединяющие две заданные точки P₁(a, A) и P₂(b, B).

Теорема 1. Для того чтобы функционал (2), определённый на множестве функций y=y(x), имеющих непрерывную первую производную, и удовлетворяющих граничным условиям (1), достигал на заданной функции y(x) экстремума, необходимо, чтобы эта функция удовлетворяла уравнению Эйлера:

. (3)

Интегральные кривые уравнения Эйлера называют экстремалями (лагранжевыми кривыми). Уравнение Эйлера в развёрнутом виде:

(4)

Уравнение (4) представляет собой дифференциальное уравнение второго порядка, так что его общее решение должно зависеть от двух произвольных постоянных. Значения этих постоянных, вообще говоря, определяются из граничных условий (1).

Экстремум функционала (2) может реализоваться только на экстремалях, которые удовлетворяют условиям (1).

Краевая задача: 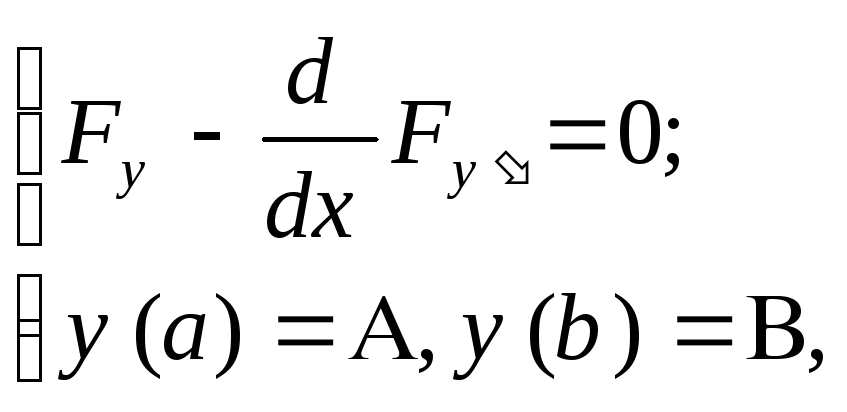(5)

не всегда имеет решение, а если решение существует, то оно может быть не единственным.

Пример 1. Найти экстремали функционала

удовлетворяющие граничным условиям

.

Решение. Уравнение Эйлера имеет вид 3x-2y=0, откуда y(x)=3/2 x. Так как экстремаль не удовлетворяет условию , то данная вариационная задача решения не имеет.

Пример 2. Найти кривые, на которых может достигать экстремума функционал .

Решение. Здесь , так что уравнение Эйлера имеет вид . Общее решение уравнения Эйлера есть . Граничные условия дают систему линейных уравнений для определения и .

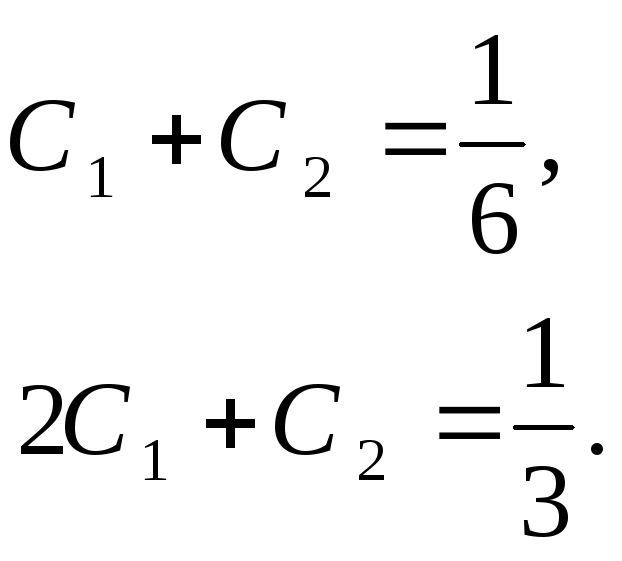
Отсюда . Следовательно, экстремум может достигаться лишь на кривой .

Пример 3. Найти экстремали функционала удовлетворяющие граничным условиям , .

Решение. Уравнение Эйлера имеет вид , его общим решением является . Используя граничные условия, получим , где - произвольная постоянная.

Таким образом, поставленная задача имеет бесчисленное множество решений.

2. Простейшие случаи интегрируемости уравнения Эйлера

1. не зависит от .

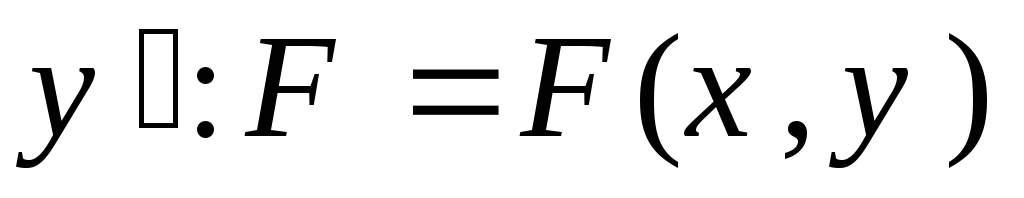В этом случае уравнение Эйлера имеет вид

. (6)

Решение этого дифференциального уравнения не содержит элементов произвола и поэтому, вообще говоря, не удовлетворяет граничным условиям , .

Лишь в исключительных случаях, когда кривая (6) проходит через граничные точки и существует кривая, на которой может достигаться экстремум.

2. зависит от линейно, то есть,.

Уравнение Эйлера в этом случае имеет вид:

. (7)

Полученное уравнение, как и в случае (1), является конечным, а не дифференциальным уравнением. Кривая, определяемая уравнением , вообще говоря, не удовлетворяет граничным условиям, и, значит, вариационная задача, как правило, не имеет решения в классе непрерывных функций. Если в некоторой области  плоскости , то выражение является полным дифференциалом и функционал

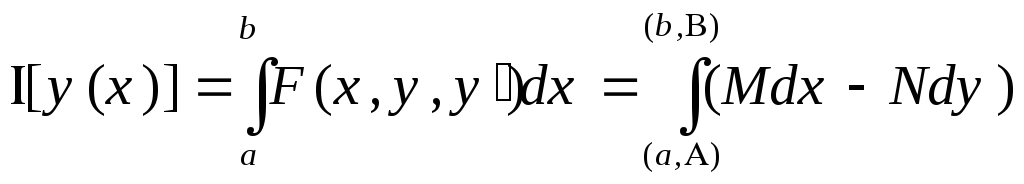
не зависит от пути интегрирования: значение функционала одно и тоже на допустимых кривых. Вариационная задача теряет смысл.

3. зависит лишь от 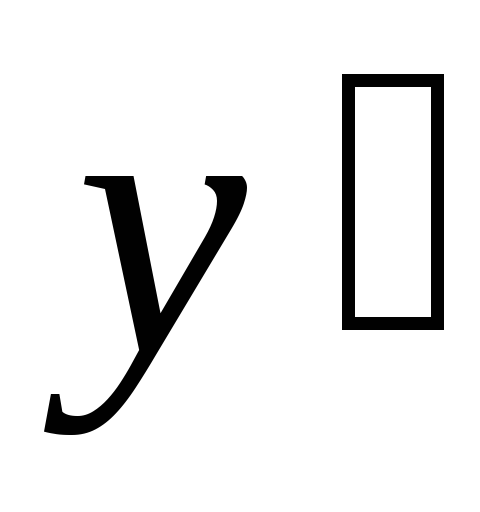, то есть .

Уравнение Эйлера имеет вид

.

В этом случае экстремалями являются прямые всевозможные линии

, (8)

где и - произвольные постоянные.

4. не зависит от , то есть .

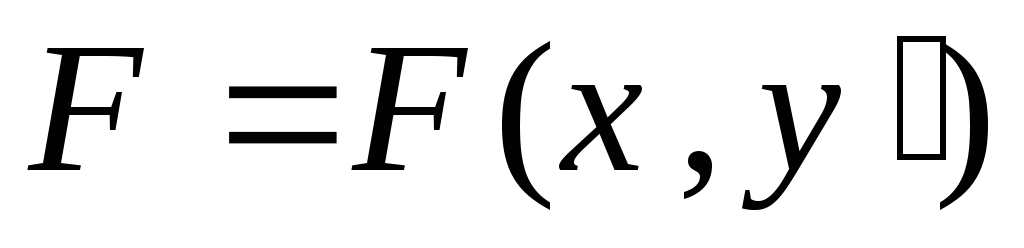В этом случае уравнение Эйлера , откуда

(9)

где - произвольная постоянная.

Уравнение (9) есть дифференциальное уравнение первого порядка. Интегрируя его, находим экстремали задачи.

5. F не зависит явно от , то есть .

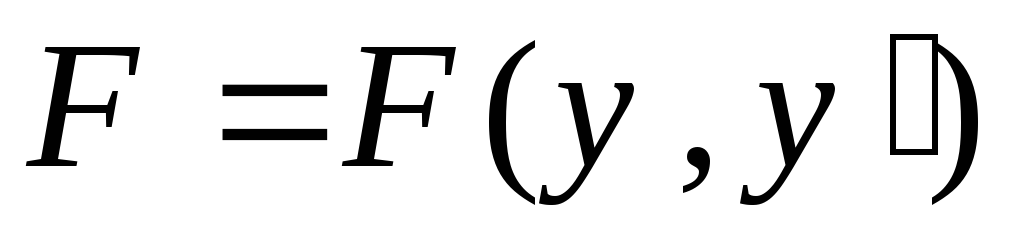В этом случае уравнение Эйлера принимает вид

.

Умножив обе части этого уравнения на , в левой части получим точную производную, то есть , откуда

, (10)

где - производная постоянная. Это уравнение может быть проинтегрировано путём разрешения относительно и разделения переменных или путем введения параметра.

Контрольные вопросы:

1. Чем отличается основная задача вариационного исчисления от конечномерной задачи?

2. Дайте графическое истолкование основной задачи вариационного исчисления.

3. Может ли вариационная задача иметь бесчисленное множество решений?

4. В каких случаях вариационная задача не имеет решений?

5. Является ли экстремаль решением основной задачи вариационного исчисления?

6. В каких случаях экстремальные кривые вырождаются в прямые?

Задание к лабораторной работе № 10.

Найти экстремали функционалов, удовлетворяющие заданным граничным условиям.

При решении задач используйте формулы (6)-(10) пункта 2.

1. ,

2. ,

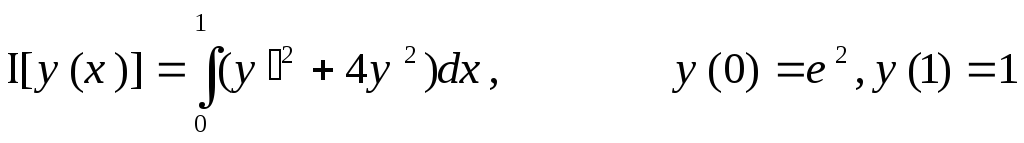3. ,

4. ,

5. ,

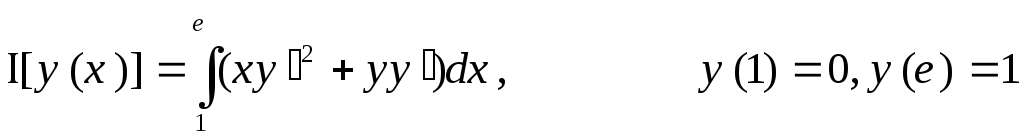6. ,

7. ,

8. ,

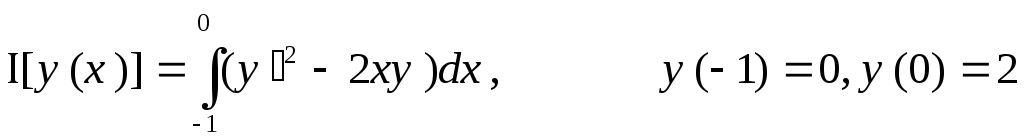9. ,

10. ,

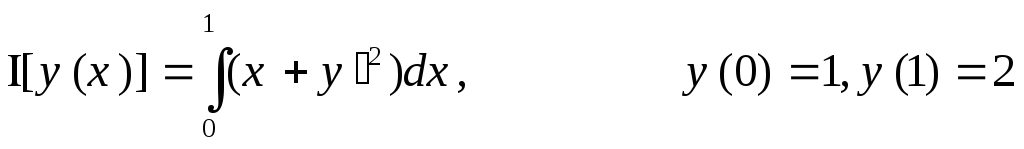11. ,

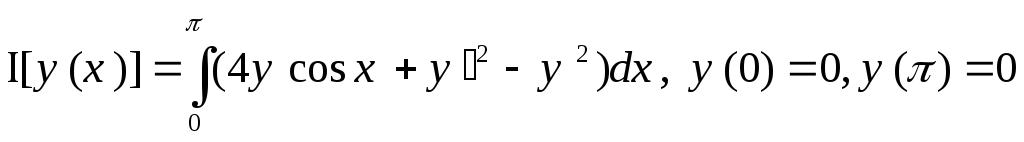12. ,

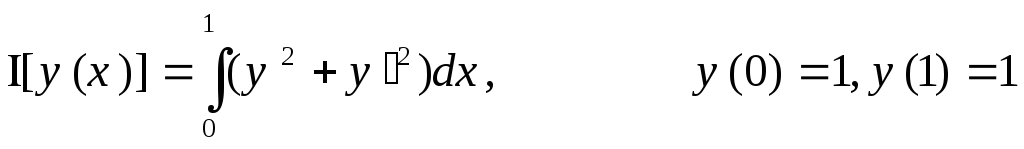13. ,

14. ,

15 ,

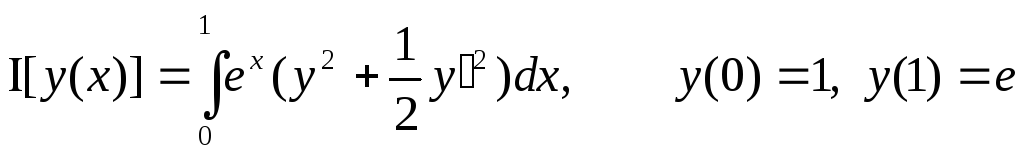16. ,

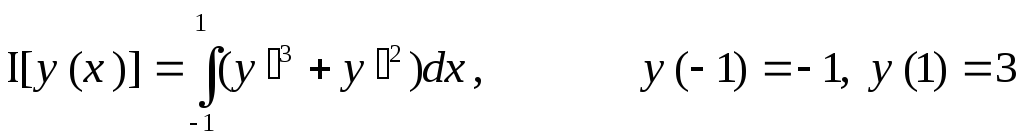17. ,

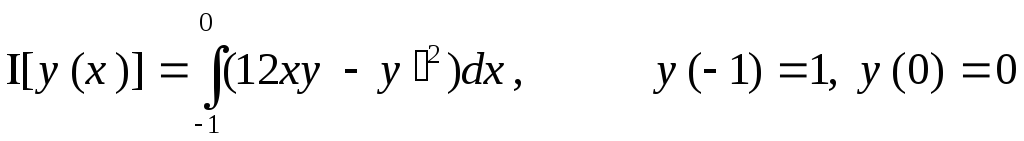18. ,

19. ,

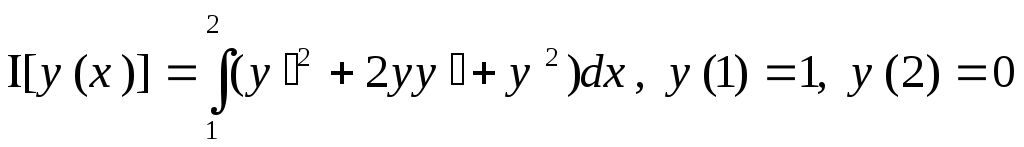20. ,

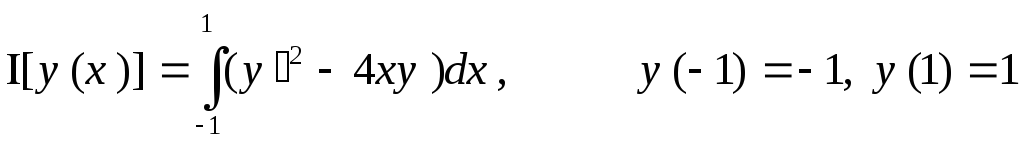21. ,

22. ,

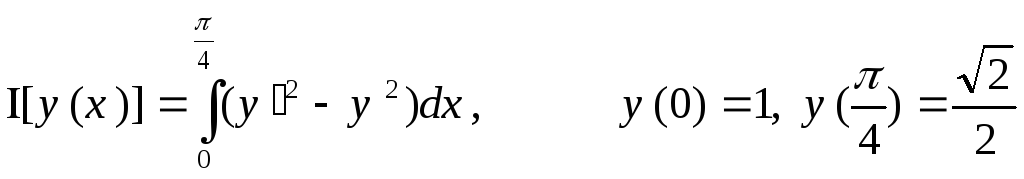23. ,

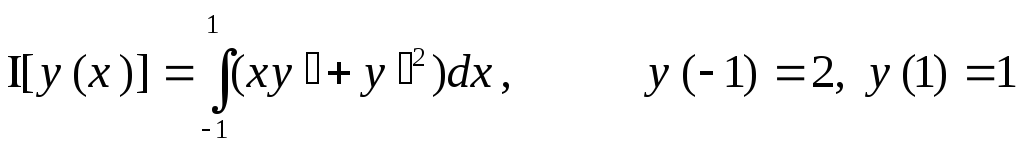24. ,

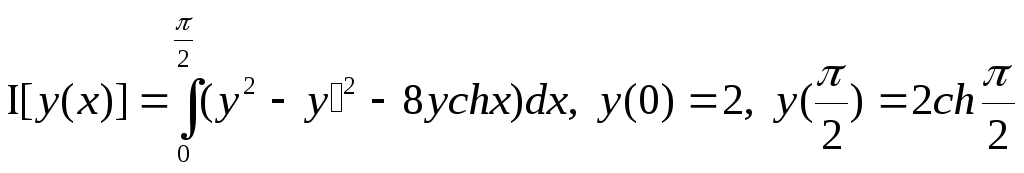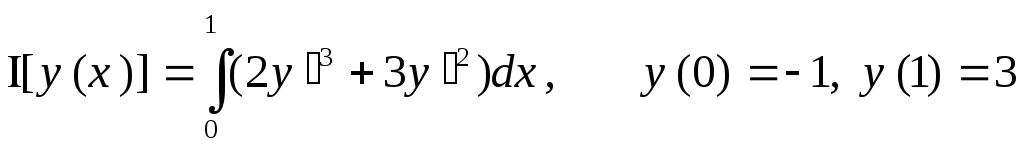25. .

57

Простейшая задача вариационного исчисления. Уравнение Эйлера. cтр.