
L_R_опт управ 13
.DOC
Лабораторная работа №13
Тема: ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА В ОПТИМАЛЬНОМ УПРАВЛЕНИИ
Цель работы: Ознакомиться с основным методом теории оптимального управления - принципом максимума Понтрягина; овладеть методикой решения задач оптимального управления.
1. Принцип максимума для простейшей задачи терминального управления
l.1. Постановка задачи. Основные определения.
Пусть движение некоторого объекта описывается уравнением
![]()
![]() ,
,
![]() ,
(1)
,
(1)
где
![]() вектор
состояния
вектор
состояния
![]() ;
;
![]() вектор
управления
вектор
управления![]() ;
;
![]() скаляр
(время);
скаляр
(время);
![]() начальный
момент и состояние;
начальный
момент и состояние;
![]() конечный
момент времени.
конечный
момент времени.
Относительно
функции
![]() будем предполагать, что она непрерывна
по аргументу вместе с функцией
будем предполагать, что она непрерывна
по аргументу вместе с функцией
![]() .
Допустимым
управлением
назовём
.
Допустимым
управлением
назовём
![]() -мерную
кусочно-непрерывную функцию
-мерную
кусочно-непрерывную функцию
![]() ,
принимающую значения из множества
,
принимающую значения из множества
![]()
![]() -мерного
пространства. Каждому допустимому
управлению
-мерного
пространства. Каждому допустимому
управлению
![]() соответствует
соответствует
![]() -некоторое
решение уравнения (допустимая
траектория).
-некоторое
решение уравнения (допустимая
траектория).
Качество
процесса
![]() оценим величиной
оценим величиной
![]() (2)
(2)
где
![]() -
скалярная величина класса
-
скалярная величина класса
![]() .
Функцию (2) назовём критерием
качества процесса.
.
Функцию (2) назовём критерием
качества процесса.
Простейшая задача оптимального управления: среди допустимых управлений найти то, на котором критерий качества (2) достигает оптимального значения.
Решение
задачи - управление
![]() называется оптимальным
управлением,
траектория
называется оптимальным
управлением,
траектория
![]() системы (1), соответствующая управлению
системы (1), соответствующая управлению
![]() -
оптимальной
траекторией.
-
оптимальной
траекторией.
Теорема
1. (принцип максимума Понтрягина). Пусть
![]() -
оптимальное управление простейшей
задачи
-
оптимальное управление простейшей
задачи
![]() ,
при движении объекта по траектории
описываемой системой дифференциальных
уравнений
,
при движении объекта по траектории
описываемой системой дифференциальных
уравнений
![]() ,
,
![]() ,
,
![]() .
.
![]() оптимальная
траектория,
оптимальная
траектория,
![]() -решение
уравнения
-решение
уравнения
![]() при
при
![]() (3)
(3)
Тогда выполняются условия максимума
![]() (4)
(4)
2.Сведение исходной задачи к краевой
Принцип
максимума является необходимым, условием
оптимальности. Если исключить управление![]() из условия максимума, то есть найти
такую функцию
из условия максимума, то есть найти
такую функцию
![]() ,
что
,
что
![]() и подставить результат в уравнение (I),
(3), то получим следующую краевую задачу
для системы из
и подставить результат в уравнение (I),
(3), то получим следующую краевую задачу
для системы из
![]() уравнений (краевая задача):
уравнений (краевая задача):
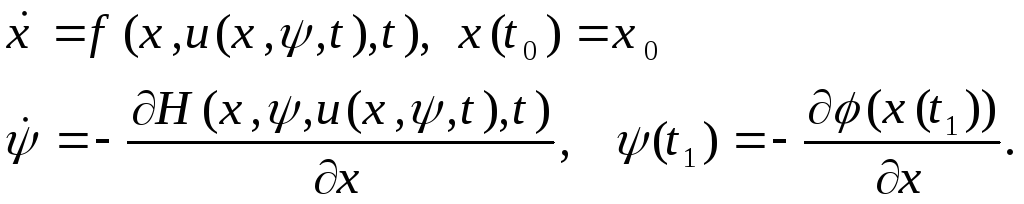 (5)
(5)
Таким образом, если задача (1), (2) имеет решение, то оптимальная траектория находится среди решений краевой задачи (5). В сведении вариационной задачи (задача минимизации функционала) к краевой задаче для обыкновенных дифференциальных уравнений и состоит конечный результат применения принципа максимума к задаче оптимального управления.
В общем случае принцип максимума не является достаточным условием оптимальности: ему могут удовлетворить и не оптимальные управления.
3. Простейшая задача с нефиксированной продолжительностью процесса
Пусть
момент
![]() окончания процесса в системе
окончания процесса в системе
![]() нефиксирован.
Тогда простейшая задача несколько
изменится. Допустимыми управлениям
называются
нефиксирован.
Тогда простейшая задача несколько
изменится. Допустимыми управлениям
называются
![]() -мерные
функции
-мерные
функции
![]() ,
(6)
,
(6)
которые
непрерывны всюду при
![]() за исключением, возможно, конечного
числа точек на каждом ограниченном
отрезке, где они имеют разрывы первого
рода. Критерий качества теперь может
явно зависеть от длительности процесса.
за исключением, возможно, конечного
числа точек на каждом ограниченном
отрезке, где они имеют разрывы первого
рода. Критерий качества теперь может
явно зависеть от длительности процесса.
![]() .
(7)
.
(7)
Задача
оптимальности состоит в поиске среди
![]() и доступных управлений оптимального
момента
и доступных управлений оптимального
момента
![]() и оптимального управления
и оптимального управления
![]() ,
на которой критерий качества (7) достигает
минимального значения
,
на которой критерий качества (7) достигает
минимального значения
![]()
Теорема
2. Для
того, чтобы число
![]() и управление
и управление
![]() ,
,
![]() доставляли решение задаче (1),
(6),
(7)
необходимо, чтобы выполнялись условия:
доставляли решение задаче (1),
(6),
(7)
необходимо, чтобы выполнялись условия:
![]()
![]()
![]() .
.
Здесь
![]() -оптимальная
траектория (решение уравнения (1) при
-оптимальная
траектория (решение уравнения (1) при
![]() )
)
![]() -решение
уравнения
-решение
уравнения
![]() при
при
![]() .
.
4. Условие трансверсальности
При изучении задач оптимизации с ограничениями на концы допустимых траекторий появляются дополнительные условия оптимальности для концов траектории, называемые условиями трансверсальности.
4.1. Ограничения типа неравенств
Усложним простейшую задачу добавлением ограничений на правый конец допустимой траектории. Рассмотрим процесс, описываемый уравнением (1).
Как
в основной задаче оптимального управления
будем рассматривать в качестве допустимого
управления
![]() -мерно-кусочно-непрерывную
функцию
-мерно-кусочно-непрерывную
функцию
![]() удовлетворяющую ограничению
удовлетворяющую ограничению
![]() .
.
Пусть
![]() - вещественные функции, определённые
на
- вещественные функции, определённые
на
![]() и
и
![]() функции
класса
функции
класса![]() .
Зададим
область
.
Зададим
область
![]() .
.
Будем
искать допустимое управление
![]() ,
,
![]() со значениями из заданного множества
со значениями из заданного множества
![]()
![]() -
мерного пространства, для которых
траектория
-
мерного пространства, для которых
траектория
![]() ,
,
![]() системы (1) в момент
системы (1) в момент
![]() попадают в множество
попадают в множество
![]() (задача с ограничениями на правый конец
траектории).
(задача с ограничениями на правый конец
траектории).
Теорема
3. Пусть
![]() и
и
![]() соответствующие оптимальные управление
и траектория в задаче терминального
управления с ограничениями на правый
конец траектории. Тогда найдутся такие
числа
соответствующие оптимальные управление
и траектория в задаче терминального
управления с ограничениями на правый
конец траектории. Тогда найдутся такие
числа
![]() и не все равные нулю одновременно, такие,
что вдоль оптимальной траектории
и не все равные нулю одновременно, такие,
что вдоль оптимальной траектории
![]() и решения
и решения
![]() сопряженной системы уравнений
сопряженной системы уравнений
![]() ,
выполняются условия:
,
выполняются условия:
1)
условия максимума
![]()
2)
условия трансверсальности
![]()
Если
имеются ограничения на левый конец
траектории, тогда найдутся
![]() - вещественные функции, определённые
на
- вещественные функции, определённые
на
![]() и
и
![]() функции
класса
функции
класса![]() .
Зададим область
.
Зададим область
![]()
Будем
искать допустимое управление
![]() ,
,
![]() со значениями из заданного множества
со значениями из заданного множества
![]()
![]() -
мерного пространства, для которых
траектория
-
мерного пространства, для которых
траектория
![]() ,
,
![]() системы (1) в момент
системы (1) в момент
![]() попадают в множество
попадают в множество
![]() (задача с ограничениями на левый конец
траектории).
(задача с ограничениями на левый конец
траектории).
Теорема
4. Пусть
![]() и
и
![]() соответствующие оптимальные управление
и траектория в задаче терминального
управления с ограничениями на левый
конец траектории. Тогда найдутся такие
числа
соответствующие оптимальные управление
и траектория в задаче терминального
управления с ограничениями на левый
конец траектории. Тогда найдутся такие
числа
![]() и не все равные нулю одновременно, такие,
что вдоль оптимальной траектории
и не все равные нулю одновременно, такие,
что вдоль оптимальной траектории
![]() и решения
и решения
![]() сопряженной системы уравнений
сопряженной системы уравнений
![]() ,
выполняются условия:
,
выполняются условия:
1)
условия максимума
![]()
2)
условия трансверсальности
![]() .
.
4.2. Ограничения типа равенств
Множество
![]() ,
задающее ограничения на правые концы
допустимых траекторий, определим как
множество точек
,
задающее ограничения на правые концы
допустимых траекторий, определим как
множество точек
![]() - мерного пространства, удовлетворяющих
уравнению
- мерного пространства, удовлетворяющих
уравнению
![]() т.
е.
т.
е.
![]() ,
(8)
,
(8)
где
![]() функции
класса
функции
класса![]() .
Допустимыми теперь будут только
траектории, которые попадают в момент
времени
.
Допустимыми теперь будут только
траектории, которые попадают в момент
времени
![]() множество (8).
множество (8).
Теорема
5. Пусть
![]() и
и
![]() соответствующие оптимальные управление
и траектория в задаче
соответствующие оптимальные управление
и траектория в задаче
![]() ,
,
![]() ,
,
![]() .
.
![]()
![]()
Тогда
найдутся такие числа
![]() не все одновременно равные нулю , такие,
что вдоль оптимальной траектории
не все одновременно равные нулю , такие,
что вдоль оптимальной траектории
![]() и решения
и решения
![]() сопряженной системы уравнений
сопряженной системы уравнений
![]() ,
выполняются условия:
,
выполняются условия:
1)
условия максимума
![]()
![]() ;
;
2)
условия трансверсальности
![]() .
.
5. Задачи оптимального управления типа Лагранжа и Больца
Пусть
движение объекта описывается уравнением
(1). Среди допустимых управлений найти
оптимальное
![]() ,
,
![]() ,
доставляющее минимум критерию качества
,
доставляющее минимум критерию качества
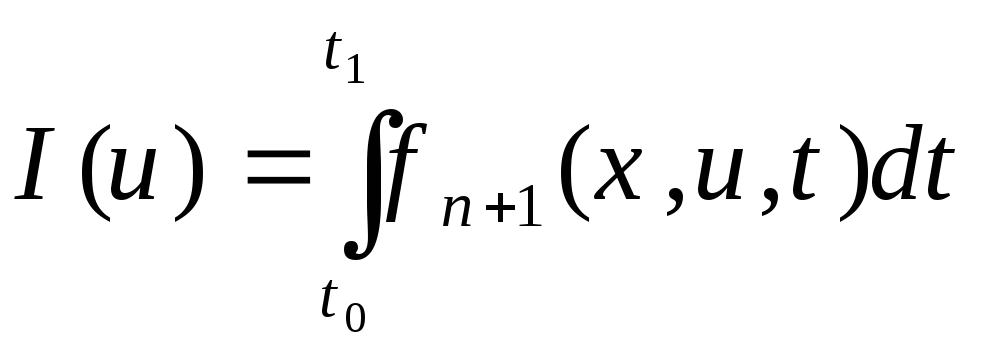 .
(9)
.
(9)
Эта задача называется задачей оптимального управления Лагранжа.
Если критерий качества заменить на
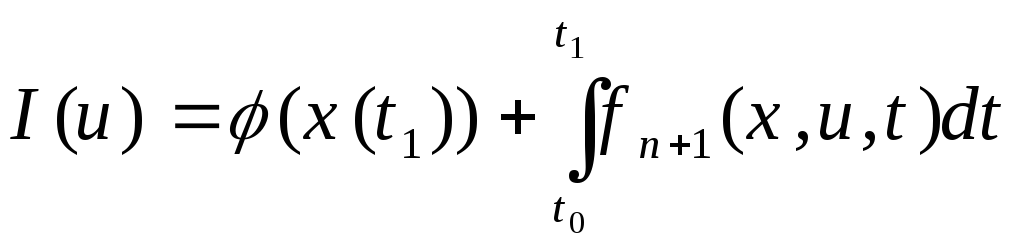 ,
(10)
,
(10)
то получим задачу оптимального управления типа Больца.
Теорема
6. Для
оптимальности задачи Лагранжа, необходимо,
чтобы при решении
![]() и
и
![]() систем
систем
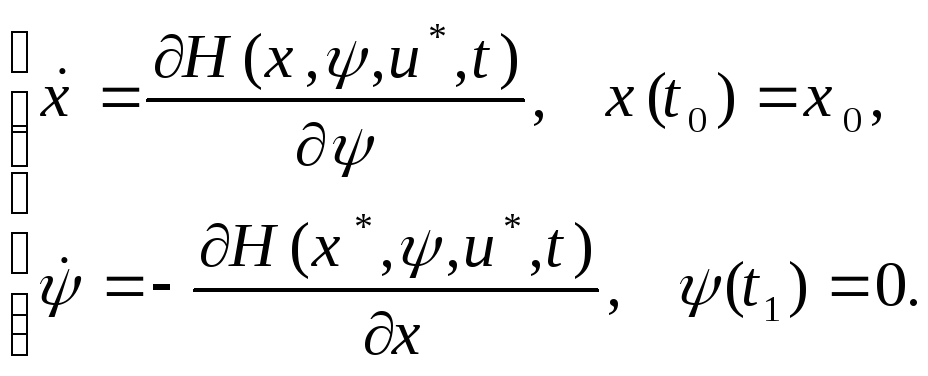
![]()
выполнялось
равенство:
![]() .
.
Теорема
7. Пусть
![]() ,
,
![]() -решение
задачи типа Больца c
подвижным правым концом
-решение
задачи типа Больца c
подвижным правым концом![]() ,
,
![]() ,
,![]() ,
,![]() .
.
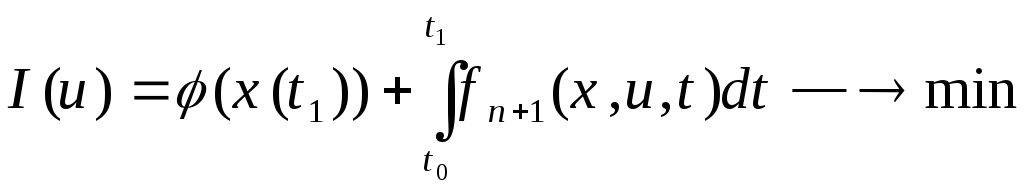 .
.
Тогда
найдутся числа
![]() не равные одновременно нулю, такие, что
выполняются:
не равные одновременно нулю, такие, что
выполняются:
I)
условие максимума
![]()
![]() ;
;
2)
условие трансверсальности
![]() ,
,
где
![]() ,
,![]() -
оптимальная траектория;
-
оптимальная траектория;
![]() ,
,
![]() решение
сопряженного уравнения
решение
сопряженного уравнения
![]()
с
граничным условием
![]() .
.
Теорема
8. Пусть
![]() ,
,![]() ,
,
![]() -решение
задачи
-решение
задачи
![]() ,
,
![]() ,
,![]() .
.
 .
.
Тогда
найдутся числа
![]() не равные одновременно нулю, такие, что
выполняются:
не равные одновременно нулю, такие, что
выполняются:
I)
условие максимума
![]()
![]() ;
;
2)
условие трансверсальности
![]() ;
;
3)
условие
на конечный момент
![]()
![]() ,
,
где
![]() ,
,![]() -
оптимальная траектория;
-
оптимальная траектория;
![]() ,
,
![]() решение
сопряженного уравнения
решение
сопряженного уравнения
![]() с
граничным условием
с
граничным условием
![]() .
.
6. Задача оптимального быстродействия с закрепленными концами
В силу особой распространенности задачи быстродействия сформулируем для нее отдельно необходимые условия оптимального управления.
Теорема
9. Для
того, чтобы допустимое управление
![]() ,
,
![]() ,
было решением задачи быстродействия
,
было решением задачи быстродействия
![]() ,
,
необходимо, чтобы выполнялись:
-
условие максимума
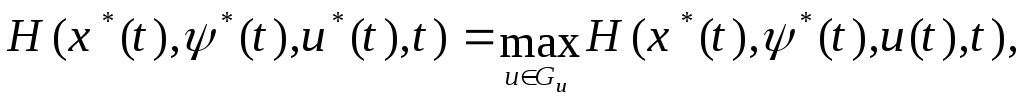
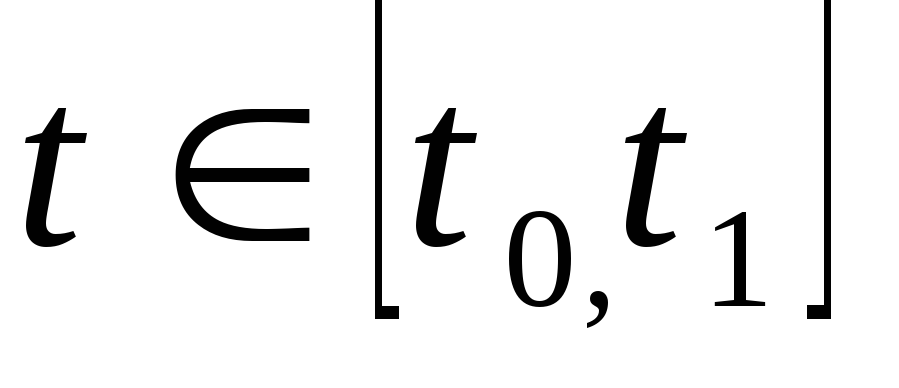 ,
,
для
некоторого нетривиального решения
![]() системы
системы
![]()
-
условие для оптимального момента

Пример
1. Перевести
точку
![]() из состояния
из состояния
![]() на множество
на множество
![]() быстрейшим
образом, предполагая, что движение точки
подчиняется уравнениям
быстрейшим
образом, предполагая, что движение точки
подчиняется уравнениям![]() причем
причем
![]() .
Начальный момент времени
.
Начальный момент времени
![]()
Решение.
Используем теорему 4. В нашем случае
![]() с
с
граничными
условиями трансверсальности
![]() .
.
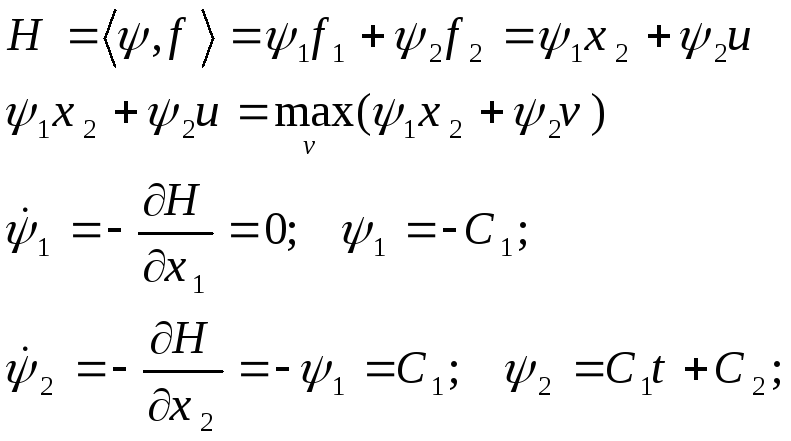
Условие максимума
![]()
![]() для некоторого нетривиального решения
для некоторого нетривиального решения
![]() системы
системы
![]()
Условие
для оптимального момента
![]() Используем начальные условия
Используем начальные условия
![]() .
Решаем системы
.
Решаем системы
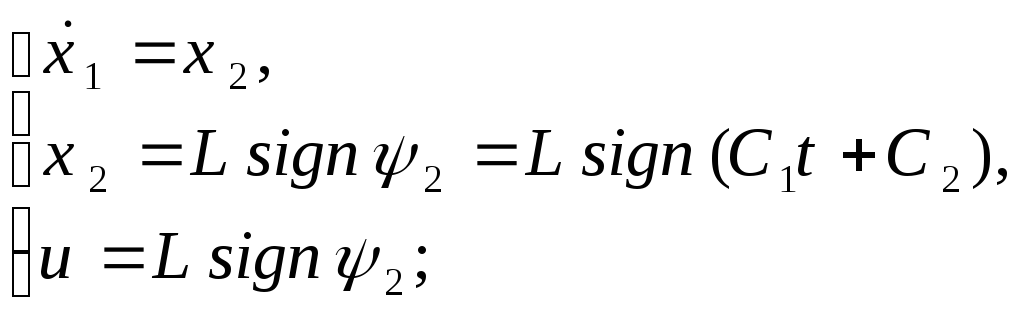 со знаком “+”,
со знаком “+”,
![]() .
.
Пример 2. Пусть требуется минимизировать функционал
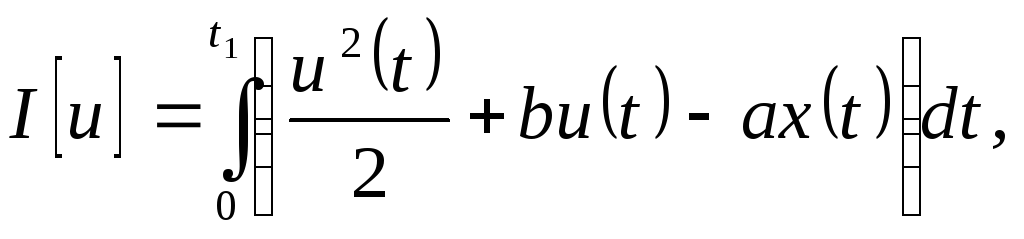
при условиях:
![]() .
.
Решение. Строим функцию Гамильтона:
![]() .
.
Условие
максимума:
![]()
![]() ,
,
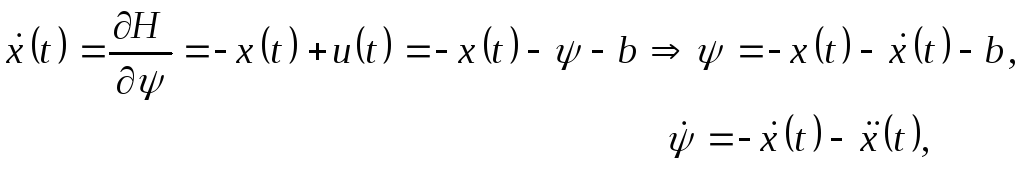
![]() .
.
Следовательно:
![]() .
.
Решим это дифференциальное уравнение:
![]()
![]() ,
,
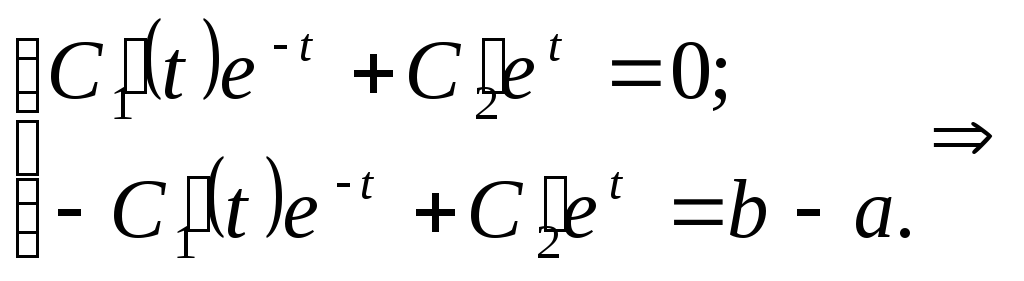
![]() ,
, ![]()
![]() ,
,
![]() .
.
Воспользуемся
граничными условиями для нахождения
![]() и
и
![]() :
:
![]()
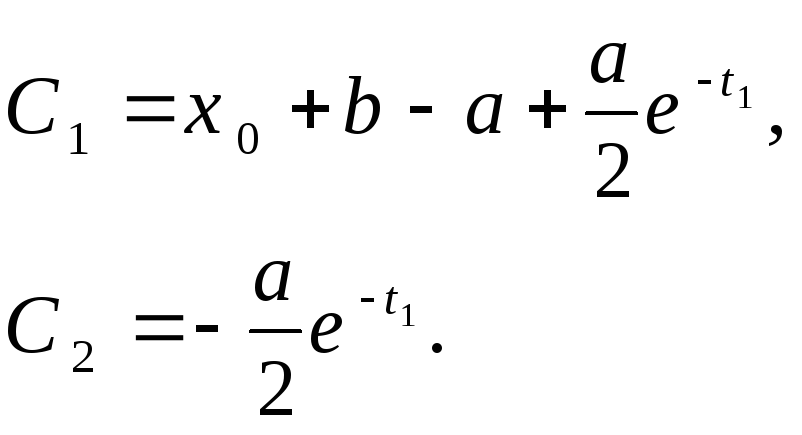
Тогда траектория соответствующая оптимальному управлению примет вид:
![]() ,
,
![]() .
.
Оптимальное
управление:
![]() .
.
Задание к лабораторной работе №13.
Минимизировать функционалы
1.![]() ,
, ![]() .
.
![]() ,
,
2.
![]() ,
, ![]() .
.
3.
![]() ,
, ![]() .
.
4.
![]() ,
, ![]() .
.
![]() ,
,
5.
![]() ,
, ![]() .
.
6.
![]() ,
, ![]() .
.
7.
![]() ,
, ![]() .
.
8.
![]() ,
, ![]() .
.
![]() ,
,
9.
![]() ,
, ![]() .
.
10.
![]() ,
, ![]()
