§ 5. Основные положения

И ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ.

ПРАВИЛА ЗНАКОВ

Основу законов геометрической или лучевой оптики состав­ляют понятия о светящейся точке и световом луче.

При распространении света, как известно, имеют место ин­терференция, дифракция и другие явления физической оптики, характеризующие волновую природу света, когда точечному излучению соответствует волновая поверхность, которая рас­пространяется от источника света в виде электромагнитных ко­лебаний. Однако многие оптические явления можно рассмат­ривать исходя из представления, что оптическое излучение распространяется вдоль нормалей к волновой поверхности, на­зываемых лучами, т. е. не принимать во внимание дифракцию и интерференцию.

Раздел физической оптики, основывающийся на этом пред­ставлении, называется геометрической оптикой. В геометриче­ской оптике источ-ником света считается светящаяся точка, как геометрическая точка, не имеющая размеров, из которой световая энергия лучами распространяется во все стороны, а световой луч—геометрическая линия, прямая (нормаль к фронту световой волны), вдоль которой распространяется световая энергия.

Такое представление о световом излучении является откло­нением от действительности, поэтому геометрическая оптика может рассматри-ваться лишь как предельный случай волновой оптики при длине световой волны, стремящейся к нулю, а све­тящаяся точка и световой луч являются геометрическими аб­страктными понятиями реальных физических объ-ектов.

Но, пользуясь условными понятиями светящейся точки и светового луча, можно с достаточной строгостью значительно проще представить принципы действия оптических систем на основе законов геометрической оптики, чем при помощи зако­нов волновой оптики.

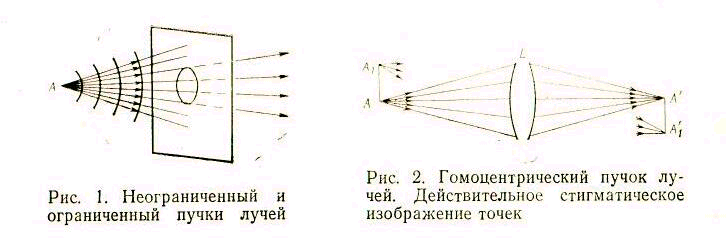
Световые лучи, исходящие из светящейся точки во все сто­роны, образуют неограниченный световой пучок. Если на пути лучей неограниченного пучка установить непрозрачную пластину с отверстием (диафрагму), то можно полу­чить ограниченный пучок (рис. 1). Пучок, лучи кото­рого имеют одну общую точку пересечения, называется гомо­центрическим пучком лучей, точка пересечения лучей—­центром пучка.

Различают сходящиеся и расходя­щиеся гомоцентрические пучки лучей. Если светящаяся точка удалена в бесконечность, то узкий пучок лучей, исходящих из этой точки, образует параллельный пучок.

Задача любой оптической системы L (рис. 2) состоит в том, чтобы преобразовать один гомоцентрический пучок лучей (на­пример исходящих из точки А) в другой, также гомоцентриче­ский пучок лучей (например сходящихся в точке А'). Центры пучков, т. е. точки А и А' соответственно, называются пред­метом и изображением. Предмет АА₁ и его изображе­ние А'А'₁ в таком случае рассматриваются как совокупности отдельных точек. Если пучок световых лучей после прохожде­ния через оптическую систему сохраняет гомоцентричность, то каждая точка предмета дает только одну точку изображения. Такое изображение называется точечным или стигмати­ческим. Пространство, в котором расположен предмет, на­зывается пространством предмета; пространство, в ко­тором расположено изображение,—пространством изо­бражения. Если лучи выходят из точки А', то эта точка будет предметом, а ее изображением будет точка А. Такие две точки, одна из которых является изображением другой, назы­ваются сопряженными точками относительно данной оптической системы. Каждому падающему лучу (пучку лучей) в пространстве предметов будет соответствовать пре­ломленный луч (пучок лучей) в пространстве изображений.

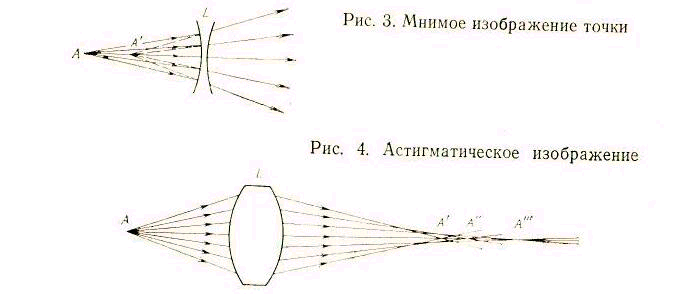
Изображение, образованное пересечением действительных лучей после выхода их из оптической системы, называется действительным изображением. На рис. 2 точки А' и А'₁—действительные изображения точек А и А₁ Изображе­ние точки А в точке А' (рис. 3), образованное пересечением про­должений, выходящих из оптической системы лучей, называ­ется мнимым изображением. Действительное изобра­жение может быть получено на экране или фотопленке. Мнимое не может быть получено на экране.

Все реальные оптические системы, как правило, строят не строгое точечное, стигматическое изображение. Если лучи от точки предмета, после выхода из оптической системы, не все пересекаются в одной точке, такое изображение называется астигматическим. На рис. 4 выходящему из точки А го­моцентрическому пучку соответствует негомоцентрический пу­чок в пространстве изображений.

В геометрической оптике часто рассматриваются лучи, иду­щие вблизи от главной оптической оси (под малым углом к ней), такие лучи называются параксиальными лучами. Пучок параксиальных лучей называется параксиальным пуч­ком.

Из опыта непосредственного наблюдения за оптическими явлениями природы установлены следующие законы, на кото­рых основывается теория геометрической оптики:

— закон прямолинейного распространения света в однород­ной среде;

— закон независимого распространения света;

— закон отражения света;

— закон преломления лучей света на границе двух про­зрачных сред;

• принцип обратимости.

Закон прямолинейного распространения света. В однород­ной и изотропной среде [Изотропной называется среда, имеющая одинаковые физические (в т. ч. и оптические) свойства по разным направлениям.] свет между двумя точками распро­страняется по прямой, соединяющей эти точки. На основе за­кона прямолинейного распространения света объясняются тени и полутени, затмения Солнца и Луны; производятся все высо­коточные геодезические и астрономические наблюдения.

Закон независимого распространения света. В геометриче­ской оптике предполагается, что в сложном световом потоке отдельные лучи не влияют друг на друга и распространяются так, как будто других лучей не существует.

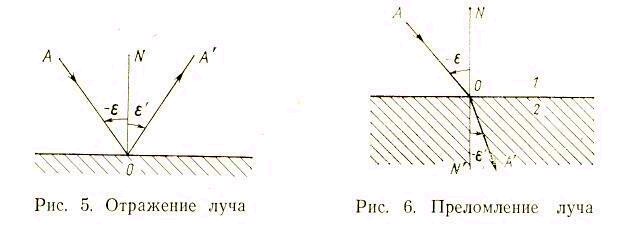
Закон отражения света. Луч падающий АО (рис. 5), луч от­раженный ОА' и нормаль N0 к полированной отражающей по­верхности в точке падения О находятся в одной плоскости; угол падения ε и угол отражения ε ' равны по абсолютной ве­личине, но противоположны по знаку:

e = - e’ (2.28)

Закон преломления лучей на границе двух прозрачных сред. При переходе из одной прозрачной среды в другую прозрачную среду луч, идущий неперпендикулярно к границе сред, изме­няет свое направление, т. е. преломляется. Падающий луч АО (рис. 6), луч преломленный ОА' и нормаль ОN к поверхности раздела в точке падения лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления для заданных оптических сред, при данных условиях (Р, t, λ), есть величина постоянная и равная относительному показателю преломления

этих сред (n_2,1).

sin e / sin e ‘ = n_2,1

где 2, 1 — вторая и первая среды.

Законы отражения и преломления света имеют первосте­пенное значение при расчете оптических систем.

Принцип обратимости. Законы преломления и отражения действуют и при обратном направлении хода лучей, т. е. вы­полняется принцип обратимости: луч преломленный может быть заменен на падающий, а падающий на преломленный; луч отраженный заменяется на падающий, а падающий на от­раженный.

Правила знаков. В соответствии с ГОСТ 7427—76 при из­ложении вопросов геометрической оптики направление распро­странения света слева направо принимается за положительное. Для отрезков и углов используются следующие правила знаков.

Для оптических систем с осевой симметрией оптическая ось (ось симметрии) принимается за ось OZ,, меридиональная плоскость (плоскость, чертежа)—за плоскость YOZ в правой системе координат.

Линейные отрезки в направлении распространения света от выбранного начала и кверху от оптической оси положительны, в обратном направ-лении—отрицательны.

Радиусы кривизны поверхностей, ограничивающих среды, положи-тельны, если центры кривизны находятся справа от по­верхностей, и отрицательны, если центры — слева от поверх­ностей.

Углы считаются положительными, если они отсчитываются по ходу стрелки часов от установленных исходных линий (ось, нормаль и т. п.), и отрицательными—если против хода.