
- •§ 1. Предмет и задачи геодезического инструментоведения
- •§ 2 История развития геодезических приборов
- •§ 3. Требования к геодезическим приборам. Стандартизация и классификация приборов. Метрологическое обеспечение измерений.
- •§ 4. Краткие сведения из физической оптики.
- •§ 5. Основные положения
- •§ 6. Показатель преломления. Полное внутреннее отражение
- •§ 7. Принцип ферма. Оптическая длина пути
- •Оптические детали и системы в геодезических приборах плоское зеркало, системы зеркал
- •§ 9. Отражательные призмы
- •§ 10. Сферическое зеркало
- •§ 11. Центрированная оптическая система. Преломление луча сферической поверхностью
- •§ 12. Преломление луча двумя сферическими поверхностями. Линза
- •§ 13. Идеальная оптическая система
- •§ 14. Система из нескольких линз
- •Нивелиры и их основные части
- •Нивелиры самоустанавливающиеся
- •Исследование, поверки и юстировки нивелиров (стр.619)
- •Исследование и компарирование реек (стр.624)
- •Поверки и исследования теодолитов
§ 12. Преломление луча двумя сферическими поверхностями. Линза
Пусть на пути параксиального луча света, исходящего из точки А\, расположенной на общей оптической оси C2Ci, установлены две сферические поверхности с радиусами кривизны г, и —/"а (рис. 25). После преломления первой поверхностью луч А\М пойдет по направлению MN, продолжение которого пересечет оптическую ось в точке А\', на расстоянии s/, определяемом формулой Аббе (3.10),
![]()
В точке N луч снова преломится, пойдет по направлению NAs и пересечет оптическую ось в точке Ау,' на расстоянии S2/• Если бы светящаяся трчка была расположена в точке Ач', то луч A^N после преломления в точке N пошел бы по направлению NM, а изображение точки Ai' было бы мнимым и получилось бы в точке А\' на расстоянии s\'. Тогда уравнение (3.10) для этого случая записалось бы в виде
![]()
Пренебрегая толщиной вещества—величиной d, после вычитания из уравнения (3.40) уравнения (3.41) получим
![]()
или, после приведения подобных членов, имеем
![]()
Уравнение (3.42) является уравнением тонкой линзы (d=0). Запишем уравнение (3.42) в виде
![]()
Если первой средой является воздух (rti==l), а показатель преломления вещества линзы п\' обозначить через п, то получим в общем виде уравнение тонкой линзы:
![]()
При Si=oo получим формулу оптической силы тонкой линзы, помещенной в воздухе,
![]()

Подставляя \Ц' в правую часть равенства (3.44), получим в окончательном виде уравнение тонкой линзы в воздухе
![]()
Линза является самой простой центрированной оптической системой. Она состоит из двух сферических поверхностей, ограничивающих прозрачный материал (обычно стекло). В частных случаях одна из поверхностей линзы может быть плоскостью (/•==оо).
Линза называется тонкой, если ее толщина d мала по сравнению с радиусами кривизны. В тонкой линзе вершины поверхностей совпадают с главными точками и совпадают между собой, образуя центр линзы. Линия, проведенная через центр тонкой линзы и через центры кривизны поверхностей, называется оптической осью линзы. Центральную часть тонкой линзы можно принять за плоскопараллельную пластинку. Лучи, проходящие через центр линзы, практически не преломляются.
Плоскости, проходящие через фокусы линзы и перпендикулярные к оптической оси, называются фокальными плоско стям и. •
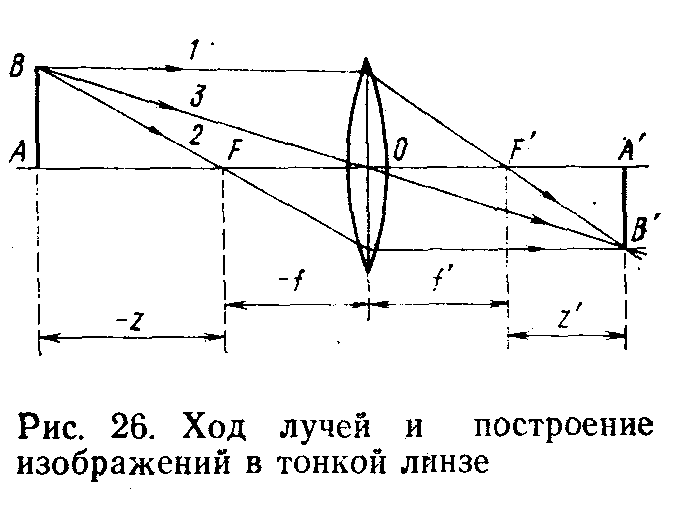
Для построения изображений в тонкой положительной линзе (рис. 26) достаточно провести; луч /, падающий на первую поверхность линзы параллельно оптической оси, который после преломления пересечет ось по другую сторону линзы в точке F', расположенной на расстоянии f от линзы; затем луч 2, падающий на линзу и проходящий через ее фокус F, этот луч выходит из линзы параллельно ее оптической оси и луч 3, проходящий через оптический центр линзы, не изменяющий своего направления
Формулы параксиальной оптики, полученные в § 11, применимы к оптическим системам с двумя преломляющими сферическими разделительными поверхностями и более.
§ 13. Идеальная оптическая система
 Простейшая
оптическая центрированная система
(лин
Простейшая
оптическая центрированная система
(лин
за) для широкого пучка лучей дает весьма несовершенное изображение. Идеальных оптических систем, которые давали бы стигматическое изображение независимо от ширины пучка, в природе не существует, за исключением плоских зеркал. Но реальные центрированные оптические системы, как правило, имеющие значительные диаметры входных отверстий, также призваны давать изображения хорошего качества, т. е. строить стигматические или близкие к стигматическим изображения. Это достигается специальными расчетами оптических систем, подбором и сочетанием линз с различными радиусами кривизны их поверхностей, разными сортами оптического стекла и определением промежутков между линзами. Теория таких расчетов достаточно громоздка. Поэтому для оценки качества реальных оптических систем их сравнивают с идеальной оптической системой.
Теория идеальной оптической системы, разработанная Гауссом в 1841 г., есть чисто геометрическая теория, устанавливающая соотношения между точками, линиями, плоскостями. Она основывается на следующих положениях:
— каждой точке пространства предметов соответствует только одна точка в пространстве изображений (точки сопряженные) ;
— каждой прямой линии пространства предметов соответствует только одна прямая линия в пространстве изображений (линии сопряженные);
— если какая-либо точка в пространстве предметов лежит на прямой, то сопряженная с ней точка также лежит на прямой, сопряженной с первой прямой;
— всякая плоскость изображается плоскостью, сопряженной с первой.
Оптическая ось идеальной центрированной системы является осью симметрии.
Теория Гаусса установила ряд так называемых кардинальных точек и плоскостей, задание которых полностью описывает все свойства оптической системы и позволяет пользоваться ею, не рассматривая реального хода лучей в системе.

Рис. 27. Ход лучей и построение изображений в идеальной оптической системе. Кардинальные плоскости и точки
На рис. 27 представлена идеальная оптическая система с двумя сферическими поверхностями. Первая сферическая поверхность с вершиной О и последняя — с вершиной О'. FOO'F'—оптическая ось системы.
Чтобы построить изображение точки через эту систему, достаточно знать положение двух пар сопряженных точек, называемых кардинальными. Это точки F и F'—передний и задний фокусы; Н и Я'—передняя и задняя главные точки*, т. е,. знать фокусные расстояния и положение главных плоскостей **.
Задняя главная плоскость Н' определяется пересечением продолжений лучей MN пространства предметов, идущих параллельно оси, и Q'F'—преломленного луча, идущего через фокус.
Передняя главная плоскость Н аналогично определится, если параллельный луч идет в пространстве изображений M'N', а преломление его QF—в пространстве предметов.
Точки пересечения главных плоскостей с оптической осью есть главные точки системы (Н'— задняя главная точка, Н—передняя главная точка).
Задний фокус системы—точка F'. Сопряженная с ней точка находится в бесконечности в пространстве предметов на оптической оси.
* Когда пфп', то в качестве кардинальных точек могут быть использованы узловые точки К и /?', проходя через которые сопряженные лучи в пространствах предметов и изображений не изменяют направления.
** Когда п=п', узловые точки совпадают с главными. Главными плоскостями называются две сопряженные плоскости, расположенные перпендикулярно к оптической оси и проходящие через главные точки. Для главных плоскостей линейное увеличение Р= +1.
Передний фокус системы—точка Р. Сопряженная с ней точка находится в пространстве изображений на оптической оси в бесконечности.
Заднее фокусное расстояние f'=H'F'—расстояние от задней главной точки до заднего фокуса.
Переднее фокусное расстояние—f=HF—расстояние от передней главной точки до переднего фокуса (отрицательное). фокусные расстояния можно выразить через высоту h и углы
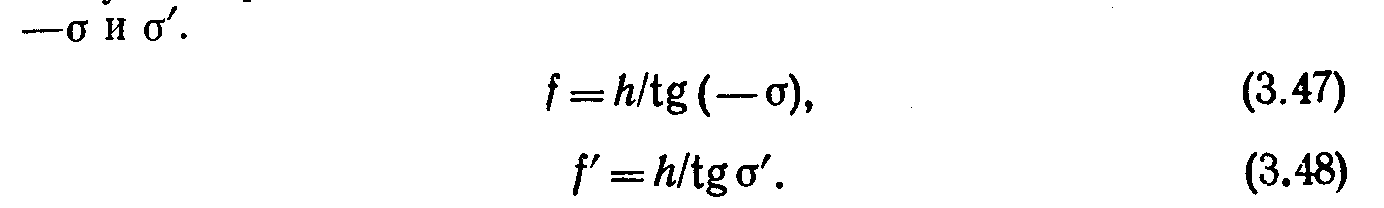
Задний и передний вершинные фокальные отрезки есть расстояния от вершин до фокусов, sp' =0 F и —Sp=OF.
Задняя и передняя фокальные плоскости проходят через фокусы перпендикулярно к оптической оси.
Расстояния задней (передней) главной плоскости от вершины последней (первой) поверхности системы

Пусть оптическая система задана кардинальными точками Н, Н' и F, F'. Получим формулы, определяющие положение всех сопряженных точек системы относительно оптической оси, фокусов и главных точек.
В пространстве предметов возьмем произвольный отрезок АВ, перпендикулярный к оптической оси. Его положение в пространстве предметов определится координатами концов отрезка, точек А и В (по оптической оси —Z; перпендикулярно к ней: О; (/).
Найдем положение сопряженного отрезка А'В' в пространстве изображений. Для этого достаточно из точки В провести два луча (один параллельно оптической оси до задней главной плоскости, далее через F'; второй через F до передней главной плоскости, далее параллельно оси, в соответствии со свойствами главных плоскостей). Пересечение лучей (точка В') есть изображение точки В. Точка А' (изображение точки А) получится как основание перпендикуляра, опущенного из точки В' на оптическую ось.
Положение изображения отрезка (точек А' и В') определится координатами: на оптической оси -{-г', перпендикулярно к оси, соответственно, О и (—у'). Положение отрезка А'В' относительно задней главной плоскости определится расстоянием s' из формулы Гаусса (3.19), справедливой, как и другие уравнения, для одной или нескольких сферических поверхностей.
В подтверждение рассмотрим подобные треугольники ABF и FHP, а также A'B'F' и F'H'P', имеем
![]()
откуда ff'=zz', получим известное уравнение Ньютона, позволяющее определить положение изображения относительно задней фокальной плоскости по известным фокусным расстояниям и заданному положению предмета относительно передней фокальной плоскости
![]()
Если значения—z и г' заменить в соответствии с рис. 27:
z=s—/, z'=s'—f, то получим формулу Гаусса (3.19), и расстояние до изображения относительно задней главной плоскости
![]()
Для оптической системы, помещенной в воздухе, крайние среды имеют показатель преломления п'-=п=\, тогда из уравнения (3.14) имеем
![]()
С учетом (3.51) формула Гаусса (3.19) обращается в формулу (3.46) тонкой линзы в воздухе.
.Уравнение (3.46), называемое формулой отрезков, используется для определения положения изображения относительно задней главной плоскости
![]()
Чтобы определить требования, которым должна удовлетворять идеальная оптическая система, когда лучи идут широким гомоцентрическим пучком, проведем луч АЕ из точки А (см. рис. 27) под произвольным углом (—ст) к оптической оси. Сопряженный с ним луч Е'А' образует с оптической осью угол о'.
Из рис. 27
![]()

Подставим эти значения в выражение (3.52), после некоторых преобразований получим
![]()
Уравнение (3.52') справедливо для идеальных систем при любых углах о и о'.
Для параксимального пучка имеется уравнение (3.31).
Сопоставляя уравнения (3.52Q и (3.31) для паракси-мальной области (когда tgo= =sin ff"o/p и tg o^s'n o= =o7p), получим уравнение f3.14). Если крайние среды одинаковы (n'^n), когда линза, например, в воздухе, то f'=—f.
 Увеличения
(линейное, продольное и угловое) идеальной
оптической системы определяются также
известными формулами: (3.24), (3.26), (3.27),
(3.36), (3.37), (3.34), (3.35), (3.38) параксиальной
оптики, т. е. идеальная система для
реальных приборов осуществима только
в параксиальной области. Наконец,
воспользуемся свойствами главных
плоскостей и кардинальных точек для
графического построения изображений.
Увеличения
(линейное, продольное и угловое) идеальной
оптической системы определяются также
известными формулами: (3.24), (3.26), (3.27),
(3.36), (3.37), (3.34), (3.35), (3.38) параксиальной
оптики, т. е. идеальная система для
реальных приборов осуществима только
в параксиальной области. Наконец,
воспользуемся свойствами главных
плоскостей и кардинальных точек для
графического построения изображений.
На рис. 28 точка А расположена в пространстве предметов на расстоянии (—z) от переднего фокуса, на оптической оси. Изображение этой точки можно построить, используя следующие два луча: луч AQ, проведенный под произвольным углом (—о) к оптической оси; луч СР, проведенный параллельно оптической оси, через точку пересечения первого луча с передней фокальной плоскостью.
После преломления в системе (по свойству главных плоскостей) второй луч обязательно пройдёт через задний фокус F'. Искомое изображение точки А' есть точка пересечения оптической оси и преломленного первого луча, проведенного через точку Q', параллельно преломленному второму лучу P'F'. Расстояние от заднего фокуса до изображения равно z'.
Правильность графического построения доказывается справедливостью формулы Ньютона по отношению точек А и А'. Из подобных треугольников CQP и ACF-F'P'H' и A'F'D' имеем
PQ/FC=CP/AF и D'F'IP'H'=F'A'IH'F'. Учитывая, что D'F'=Q'P'=QP (по построению), запишем CPIAF^F'A'IH'F',
причем CP=—f; AF=—z; A'F'=z'; H'F'^f, откуда zz'^ff, следовательно, точки А и А' действительно являются сопряженными.
Рассмотрим пример построения изображения, когда предмет находится вне оптической оси.
На рис. 28 отрезок АВ расположен перпендикулярно к главной оптической оси на расстоянии (—z) от передней фокальной плоскости. Точка В находится вне оси, а точка А на оси. Изображение отрезка АВ можно построить следующими двумя лучами, проведенными из точки В: лучом ВМ, проведенным параллельно оптической оси, который после преломления в системе (на задней главной плоскости) обязательно пройдет через задний фокус F'; лучом BN, проходящим через передний фокус F, который после преломления в системе (на передней главной плоскости) пойдет паралельно оси.
На пересечении преломленных лучей получится искомая точка В'. Перпендикуляр из этой точки на ось в пересечении с осью даст точку А'—изображение точки А.
Доказательство справедливости построения, подобно предыдущему, можно сделать, используя две пары подобных треугольников: ^ABF~AFNH и AF'B'A'^/^F'N'H'. Откуда определяется уравнение (3.23).
