Плоскость в пространстве

Виды уравнений в плоскости:

О

(

1) у

М

О

z

х

Пусть дана плоскость . Проведем к этой плоскости . Пусть , пусть единичный вектор, соответствующий вектору .

Возьмем произвольную точку М и проведем в эту точку вектор из начала координат. Очевидно, что проекция любого на

(1) нормальное уравнение плоскости в векторном виде.

(2) нормальное уравнение плоскости в координатном виде.

( 2)

z

М

у

х

Пусть дан и пусть . Пусть дана Рассмотрим , тогда и соответственно будут радиус-векторами точек и , поскольку он , лежащему в этой плоскости, поэтому =0

(3) общее уравнение плоскости в векторном виде.

(4) общее уравнение плоскости в координатном виде.

Замечание: если плоскость не проходит через начало координат, то всегда можно перейти от общего уравнения плоскости к нормальному уравнению. Для этого необходимо уравнение (4) умножить на нормирующий множитель при этом берется знак (+), если в уравнении (4) D и (-), если .

(3)Частные случаи общего уравнения плоскости.

Ах+Ву+Сz+D=0

1)Пусть D=0, тогда проходит через О(0,0,0)

2)D , Ах+Ву+Сz=-D

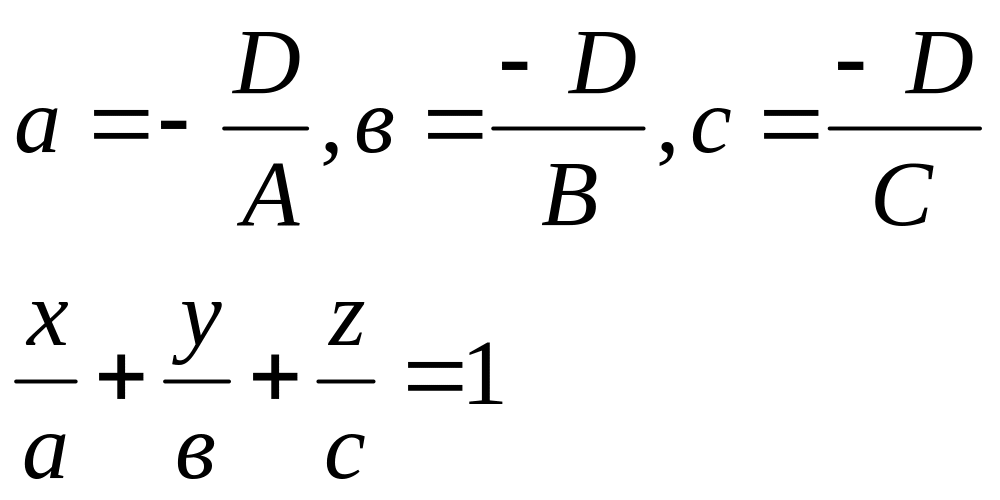
(5) уравнение плоскости в отрезках.

3)

4)

(4)Уравнение плоскости, с данным нормальным вектором, проходящий через данную точку.

Запишем формулу (3):

(6)

заданная точка

данный нормальный вектор

Замечание: при разложенных А,В,С мы получим уравнения различных плоскостей, проходящих через точку М , таким образом, формула (6) задает уравнение пучка плоскостей, проходящих через точку .

Для вывода уравнений плоскости п.5,6,7 мы воспользуемся условием компланарности трех векторов, т.е. равенством нулю смешенного произведения этих векторов.

(5)Уравнение плоскости, проходящей через данную точку, параллельную двум данным векторам.

М

Легко заметить, что , , компланарны=0

(7) уравнение плоскости, проходящей через данную точку двум данным векторам.

(6) Уравнение плоскости, проходящей через две данные точки, параллельные данному вектору.

М(х,у,z)

Возьмем произвольную точку М(х,у,z) . Очевидно, что векторы , и -их смешенное произведение=0.

( , , )=0

=0

уравнение плоскости, проходящей через две данные точки, параллельные данному вектору.

(7)Уравнение плоскости, проходящей через 3 данные точки.

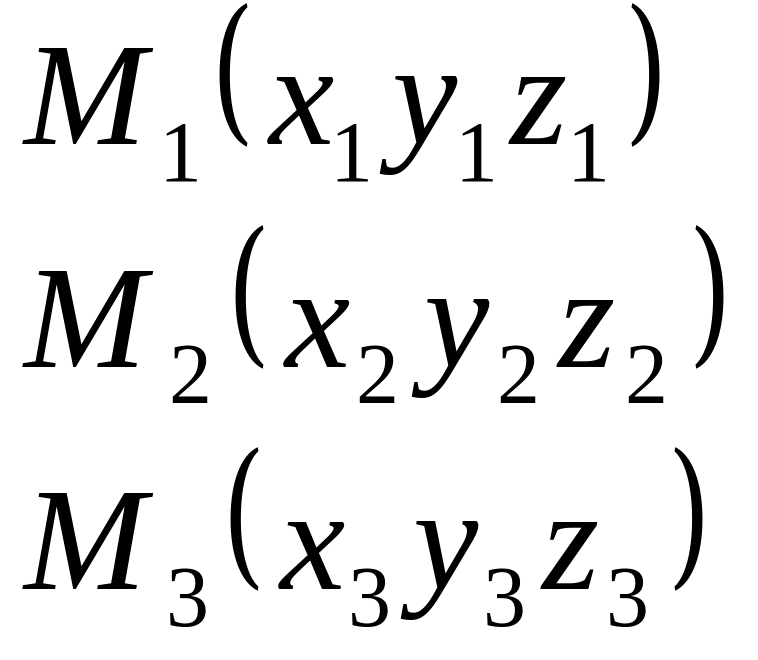
М(х,у,z)

Возьмем М . Очевидно, что векторы компланарны и определитель=0

=0 (9) уравнение плоскости, проходящей через 3 данные точки

(8)Расстояние от точки до плоскости.

=0

М

К

(10)-расстояние от точки до плоскости

(9)Взаимное расположение плоскостей.

1

)

(11) Условие параллельности плоскостей

Если , то плоскости и совпадают.

2)

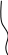
(12) условие плоскостей

3)

Линия пересечения плоскостей задается системой, состоящих из их уравнений, а cos угла между плоскостями 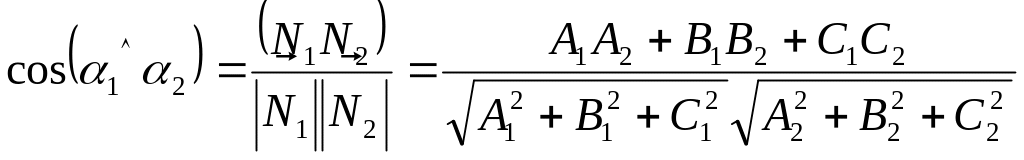(13)