Операции над векторами, разложенными по базису.

= λ_i

= μ _i

1) + = (λ_i+μ_i)

2) - = (λ_i-μ_i)

3) = ( λ_i)

Декартов базис

Пусть дана тройка векторов , , . Эта тройка векторов называется правой, если поворот вектора к вектору видимый из конца вектора осуществляется против часовой стрелки.

Если поворот осуществляется по часовой стрелке, то тройка векторов , , -левая.

Базис векторов , , называется правым, если тройка , , -правая_.

Декартовым базисом называется правый ортонормированный базис , , .

z

λ₃

М

О λ₂

у

=λ₁ +λ₂ +λ₃

λ₁

х

Вектор называется радиус-вектором точки М, т.е. радиус-вектор любой точки в декартовом базисе - это вектор, направленный из начала координат в соответствующую точку.

Деление отрезка в данном отношении

М₁(х₁у₁z₁), М₂(х₂у₂z₂)

Теорема: если точка М(х,у,z) делит отрезок М₁ и М₂ в отношении λ, то координаты данной точки выражается формулами:

х_м= ; у_м= ; z_м=

Частный случай, когда точка М делит М₁М₂ посередине:

х_м= ; у_м= ; z_м=

Скалярное, векторное и смешенное произведение векторов

Скалярное произведение:

Скалярное произведение векторов и называется число, равное произведению модулей ( )= сosφ.

Физический смысл: скалярное произведение силы на вектор =работе А этой силы при перемещении материальной точки вдоль вектора .А=( ), т.к. проекцией вектора на ось равно его модулю, умноженному на cosφ угла наклона вектора к этой оси

׀ ׀сosφ =пр

( )=׀ ׀ пр =׀ ׀пр

Алгебраические свойства скалярного произведения

1) + = + -переместительный закон относительно сложения

2)(λ )=λ( ), где λ≠0-сочетательный закон

3) ( + )= +

Доказательство: ( + )= +

( + )=пр ( + ), т.к. проекции суммы векторов = сумме проекций, то

пр ( + )=пр +пр , пр ( + )=׀ ׀(пр +пр )=׀ ׀пр +׀ ׀пр

( + )= + ч.т.д.

Геометрические свойства

1)Если ≠0 вектора и составляют острый угол, то скалярное произведение положительно.

2)Если ≠0 составляют тупой угол, то скалярное произведение отрицательно

3)Скалярное произведение=0 тогда и только тогда, когда и ортогональны

4)Cкалярный квадрат вектора равен квадрату его модуля = , то ( )= ²=׀ ׀²

Выражение скалярного произведения через координату

Теорема: пусть =(а_ха_уа_z), =(в_хв_ув_z), тогда ( )=а_хв_х+а_ув_у+а_zв_z

Доказательство: составим таблицу умножения базисных векторов

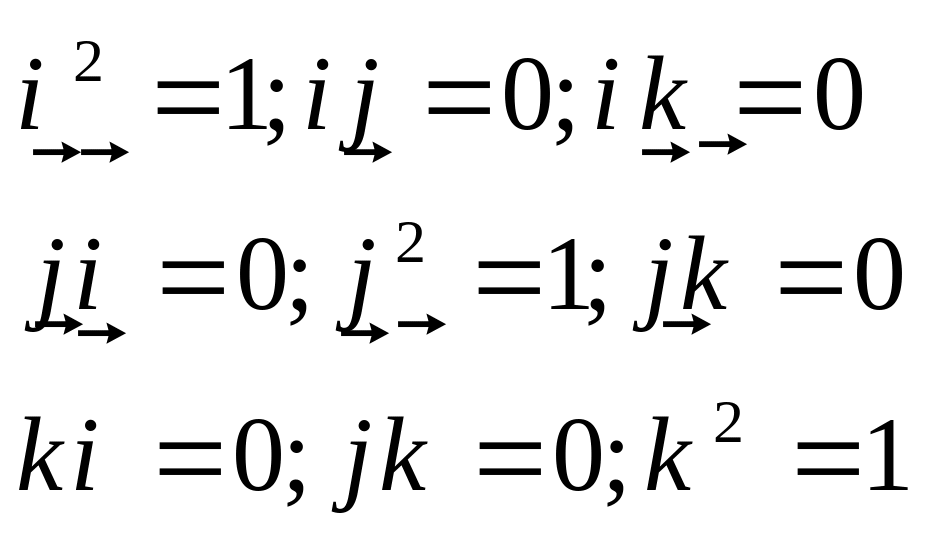
( )а_хв_хi²+а_хв_уij+а_хв_хik+…=а_хв_хi²+а_ув_уj²+а_zв_zk²=а_хв_х+а_ув_у+а_zв_z

Следствие1: необходимым и достаточным условием перпендикулярности векторов является а_хв_х+а_ув_у+а_zв_z=0

Следствие2: угол φ между векторами определяется:

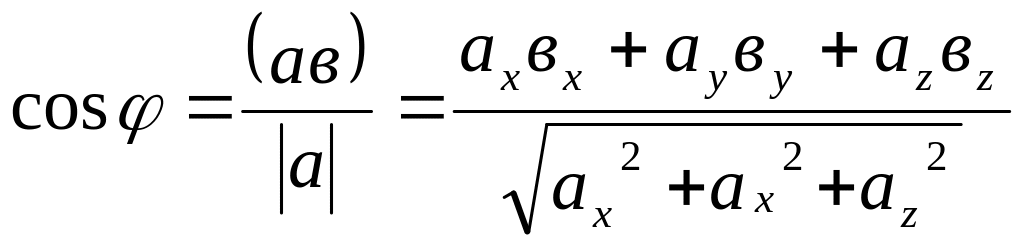
Векторное произведение:

Определение: векторным произведением векторов и называется вектор, удовлетворяющий трем условиям:

1)

2)

3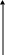 ) -правая

Физический смысл:

, если -сила, приложенная к точке В, то момент этой силы М относительно точки А = векторному произведению на .

Геометрические свойства

1)Векторное произведение=0 тогда и только тогда, когда вектора коллинеарны

2)Если векторы приведены к общему началу, то модуль векторного произведения численно равен площади параллелограмма, построенного на данных векторах, как на сторонах.

φ

S

=(-1;2;4)

=(3;1;2)

S=

S=

Векторное произведение координат

Свойства:

1) -антиперестановочное

2) -сочетательное

3) -распределительное

4)

Пример:

Смешенное произведение

Определение: смешенным произведением (векторным, скалярным) называется число = скалярному произведению одного из векторов на векторное произведение двух других.

Геометрический смысл

В пространстве каждая тройка некомпланарных векторов, приложенных к одной точке, определяет параллелепипед, ребрами которого являются данные вектора. Припишем к объему данного параллелепипеда знак , если тройка векторов правая. Знак ,

Если тройка векторов левая. Такой параллелепипед называется ориентированным.

Смешенное произведение = объему ориентированного параллелепипеда.

Смешенное произведение равно 0, тогда и только тогда, когда векторы компланарны.