Характеристики вариационного ряда

Мода вариационного ряда 2 , 5 , 5 , 6 , 7 , 9 , 10 равна … 5

Мода вариационного ряда 4 , 7 , 7 , 8 , 9 , 11 , 12 равна … 7

Мода вариационного ряда 1 , 2 , 5 , 6 , 7 , 7 , 10 равна … 7

Мода вариационного ряда 2 , 3 , 4 , 8 , 9 , 9 , 10 равна … 9

Мода вариационного ряда 3 , 4 , 5 , 6 , 10 , 10 , 12 равна … 10

Точечные оценки параметров распределения

Дана выборка объема n. Если каждый элемент выборки уменьшить в 4 раза, то выборочное среднее  … уменьшится в 4 раза

Дана выборка объема  n. Если каждый элемент выборки увеличить в 4 раза, то выборочная дисперсия … увеличится в 16 раз

Для выборки объема n вычислена выборочная дисперсия D_B=168. Тогда исправленная дисперсия S² для этой выборки равна … 196

Дана выборка объема n. Если каждый элемент выборки уменьшить в 6 раз, то выборочное среднее  … уменьшится в 6 раз

Дана выборка объема  n. Если каждый элемент выборки увеличить в 2 раза, то выборочная дисперсия … увеличится в 4 раза

По выборке объема n=100 построена гистограмма частот: Тогда значение а равно… 9

Статистическое распределение выборки имеет вид 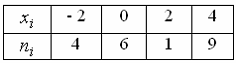Тогда относительная частота варианты X₂=0, равна … 0,3

По выборке объема n=100 построена гистограмма частот: 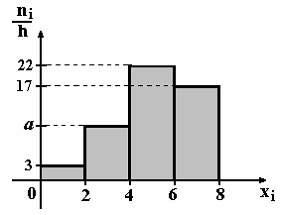Тогда значение а равно… 8

По выборке объема n=100 построена гистограмма частот: Тогда значение а равно… 21

Из генеральной совокупности извлечена выборка объема n=50: 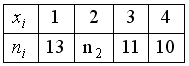Тогда n₂ равен… 16

Элементы корреляционного анализа

Выборочное уравнение парной регрессии имеет вид: , средние квадратические отклонения . Тогда коэффициент корреляции равен … 0,5

Выборочное уравнение парной регрессии имеет вид . Тогда выборочный коэффициент корреляции может быть равен… – 0,8

Выборочное уравнение парной регрессии имеет вид . Тогда выборочный коэффициент корреляции может быть равен… – 0,7

Выборочное уравнение парной регрессии имеет вид: , средние квадратические отклонения . Тогда коэффициент корреляции равен … 0,5

Выборочное уравнение парной регрессии имеет вид . Тогда выборочный коэффициент корреляции может быть равен…– 0,8

Выборочное уравнение парной регрессии имеет вид . Тогда выборочный коэффициент корреляции может быть равен… – 0,8

Выборочное уравнение парной регрессии имеет вид: , средние квадратические отклонения . Тогда коэффициент корреляции равен … 0,5

Выборочное уравнение парной регрессии имеет вид: , средние квадратические отклонения . Тогда коэффициент корреляции равен … 0,5

Проверка статистических гипотез

Если основная гипотеза имеет вид , то конкурирующей может быть гипотеза …

Если основная гипотеза имеет вид , то конкурирующей может быть гипотеза …

Если основная гипотеза имеет вид , то конкурирующей может быть гипотеза …

Если основная гипотеза имеет вид , то конкурирующей может быть гипотеза …

Если основная гипотеза имеет вид , то конкурирующей может быть гипотеза …