Полная вероятность. Формула байеса
Событие
А
может наступить лишь при условии
появления одного из двух несовместных
событий B1 и
B2,
образующих полную группу событий.
Известны вероятность
и
условные вероятности
.
Тогда вероятность P(A) равна
…
В первой урне 2 черных и 8 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна… 0,55
В первой урне 3 белых и 7 черных шаров. Во второй урне 6 белых и 4 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна… 0,45
В первой урне 3 белых и 7 черных шаров. Во второй урне 4 белых и 6 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна… 0,35
Событие
А
может наступить лишь при условии
появления одного из двух несовместных
событий B1 и
B2,
образующих полную группу событий.
Известны вероятность
и
условные вероятности 
.
Тогда
вероятность P(A)равна
…
Несовместные события A,B иC не образуют полную группу, если их вероятности равны …
,
,
Несовместные события A, B и C не образуют полную группу, если их вероятности равны …
,
,
,
,
Несовместные события A, B и C не образуют полную группу, если их вероятности равны …
, ,
, ,
Несовместные события A, B и C не образуют полную группу, если их вероятности равны …
,
,
,
,
Несовместные события A, B и C не образуют полную группу, если их вероятности равны …
,
,
,
,
Дискретная случайная величина
Дискретная
случайная величина Х
задана
законом распределения вероятностей
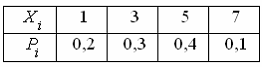Тогда
значение интегральной функции
распределения вероятностей F(4) равно
…
0,5
Функция
распределения вероятностей дискретной
случайной величины X
имеет
вид
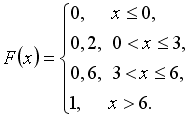Тогда
вероятность
равна
…
0,6
Дискретная
случайная величина задана законом
распределения вероятностей
Тогда
вероятность
равна
Дискретная
случайная величина задана законом
распределения вероятностей
Тогда
вероятность
равна … …
0,7
Дискретная
случайная величина Х
задана законом распределения
вероятностей
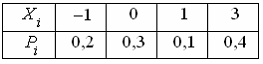Тогда
значение интегральной функции
распределения вероятностей F(2) равно
…
0,6
Дискретная случайная величина Х задана законом распределения вероятностей: Тогда математическое ожидание случайной величины равно… 5,8
Дискретная случайная величина Х задана законом распределения вероятностей: Тогда математическое ожидание случайной величины равно… 3,3
Дискретная случайная величина задана законом распределения вероятностей: Тогда её математическое ожидание равно 2,1 если …
a = 0,2; b = 0,7
Вероятность появления события А в 40 независимых испытаниях, проводимых по схеме Бернулли, равна 0,9. Тогда дисперсия числа появлений этого события равна… 3,6
Дискретная случайная величина Х задана законом распределения вероятностей Если математическое ожидание , то значение равно … 2